Как найти начальные координаты вектора (6 видео)

Нахождение координат вектора

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Содержание

Нахождение координат вектора
Примеры задач
Нахождение координат вектора через координаты точек
Как найти координаты вектора — формула, правило и примеры вычислений
Общие сведения
Проекция на ось координат
Формула координат
Примеры решения задач
Использование онлайн-калькулятора
🎬 Видео

Видео:Координаты вектора. 9 класс.Скачать

Нахождение координат вектора

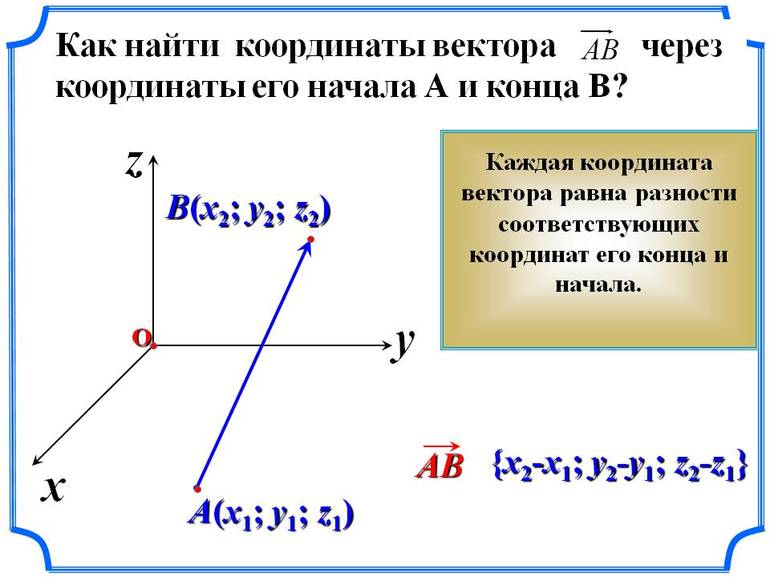
Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" AB = <B_x — A_x; B_y — A_y> » data-order=» AB = <B_x — A_x; B_y — A_y> » style=»min-width:55.0847%; width:55.0847%;»> AB = <B_x — A_x; B_y — A_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" AB = <B_x — A_x; B_y — A_y; B_z — A_z> » data-order=» AB = <B_x — A_x; B_y — A_y; B_z — A_z> «> AB = <B_x — A_x; B_y — A_y; B_z — A_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n> » data-order=» AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n> «> AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n>

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Примеры задач

Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .

Задание 2
Определим координаты точки B вектора , если координаты точки .

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB _x + A_x = 6 + 2 = 8.
B_y = AB _y + A_y = 14 + 5 = 19.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Видео:Координаты точки и координаты вектора 1.Скачать

Как найти координаты вектора — формула, правило и примеры вычислений

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Общие сведения

Под термином «вектор» принято понимать прямую с определённым направлением, ограниченную начальной и конечной точкой. Фактически это отрезок, в котором известно, где его начало и конец. Обозначают его с помощью заглавных латинских букв и стрелочкой над ними. Например, если имеется вектор, берущий начало в точке A и заканчивающийся в B, то его подписывают как AB. Но также существует и короткое обозначение — одной малой буквой со стрелкой (чертой) над ней.

При работе с отрезками приходится сталкиваться с понятием «коллинеарность». Если векторы можно совместить параллельным переносом, и линии необязательно являются равными, то их называют коллинеарными. При этом их направление не имеет значения. Если же они совпадают по нему, то такие отрезки называют сонаправленными.

Тут следует учесть, что отрезки будут направлены в одну сторону лишь только тогда, когда их лучи находятся по одну сторону от прямой, объединяющей их начала. Когда векторы коллинеарны и не сонаправлены, то они противоположные. Осюда можно сформулировать правило, что два ненулевых вектора являются коллинеарными, если они располагаются на одной или на параллельных прямых. Причём точка считается коллинеарной любому отрезку.

При работе с отрезками можно выполнять различные арифметические операции на основании их свойств. Математические правила нахождения положения общего вектора называются линейными. Выделяют следующие действия над ограниченными прямыми:

Суммирование — при сложении двух векторов образуется новый, если начальная точка совпадает с началом первого вектора, а конечная — с концом второго. Это правило работает при условии, что складываемые вектора имеют общую точку.
Вычитание — для нахождения разности нужно соединить конечные точки двух отрезков. Эта новая линия и будет являться вектором разности. Для выполнения этого правила необходимо, чтобы отрезки выходили из одной точки.
Умножение — существует три вида произведения векторов: скалярное, векторное и смешанное. Для первого и третьего вида в ответе получится число, а второго — вектор.

Кроме того, вектор можно умножить на число или разложить на составляющие компоненты. Всё это позволяет построить базисный отрезок для нахождения в дальнейшем его координат. При этом если существует перпендикулярность двух векторов, то отрезок к направляющей ограниченной линии называют нормальным или ортогональным.

Видео:11 класс, 2 урок, Координаты вектораСкачать

Проекция на ось координат

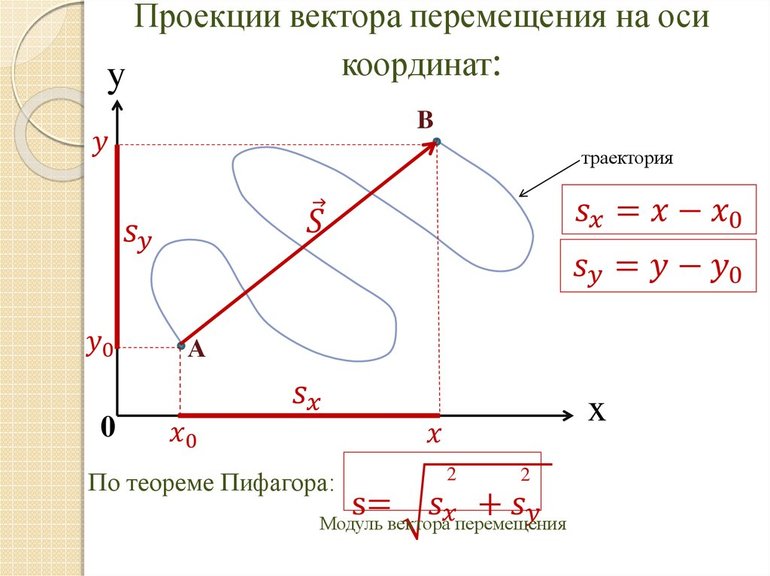
Определить координаты отрезка возможно различными способами. Один из них — использование проекции. Другими словами, изображаются в координатных плоскостях начало и конец вектора, которые соединяются прямой линией. Откладывать расположение точек нужно в соответствии с используемым масштабом. После с помощью перпендикулярных координатным осям линий на них переносят расположение начала и конца вектора, то есть как бы проецируют отрезок на оси.

При этом если направление перенесённого вектор совпадает с направлением оси, то проекция обозначается со знаком плюс, если же оно противоположное — со знаком минус. Обозначают перенос отрезков символом ПР. Существуют несколько свойств, характерных для проекции:

Если в плоскости находится два и более отрезка, равных между собой, то их проекции на одну и ту же ось будут одинаковыми.
Два отличающихся на величину m отрезка при проецировании будут равными, если проекцию одного из них увеличить или уменьшить на это число: ПР (mAB) = mПР (AB).
Проекция отрезка AB на ось P может быть определена как произведение ограниченной линии на косинус угла между ней и направлением оси в положительную сторону от этой оси: ПР (АB) = |AB| * cos (AB;P).
Проекция, полученная сложением двух отрезков на произвольно выбранную ось, равняется сумме перенесённых векторов на эту же ось.
Серединой проекции называют равноудалённое расстояние от двух концов отрезка, перенесённого на координатную ось. Определяется она как (A + B) / 2. При этом всегда совпадает с действительной серединой вектора.

Если отрезок располагается перпендикулярно оси, то его проекцией будет точка. Для декартовой системы координат в записи вектора на одном из мест будет стоять ноль. Например, AB (0; 1) или AB (-3; 0). Для задания направления в пространстве применяют так называемый единичный вектор.

Другими словами, он является отрезком нормирования пространства и обозначает масштаб проекции. Его выбирают в качестве базисного вектора, что заметно помогает упростить расчёты. Для того чтобы его вычислить, необходимо вектор разделить на длину: e = AB / | AB |. Такая операция называется нормированием.

Видео:90. Координаты вектораСкачать

Формула координат

При построении отрезка единичный вектор выбирается исходя из удобства размещения его в плоскости. Начальная и конечная точка могут быть определены в координатной плоскости. Чаще всего для этого используется декартова система координат. К расположениям осей жёстких требований нет, но принято по горизонтали рисовать ось икс в правом направлении, а по вертикали снизу вверх — ось игрек. Пересекаются эти оси между собой под прямым углом и место их пересечения называют началом отсчёта. В этой точке координата записывается как (0, 0).

Задать координаты, значит, присвоить точке два числа. Так, если точка имеет координаты x = 4; y = -2, то обозначаться она будет как A (4, -2). Ось от нуля в направлении икса называется абсциссой, а совпадающая с игреком — ординатой. В плоскости каждая точка заданного отрезка характеризуются двумя значениями. Одно из них соответствует оси ординат, а другое абсцисс. Например, A (1, 5); B (3, 2). Здесь единица и тройка соответствуют значению точек на оси икс, а пятёрка и двойка — на оси игрек.

Исходя из этого, чтобы нарисовать вектор на плоскости, нужно узнать координаты его начальной и конечной точек, а также направление. Для получения рисунка вектора нужно просто соединить эти две точки. Из знания значений, ограничивающих точки отрезка, довольно легко определить координаты вектора.

Существует простое правило, которое гласит, что для этого необходимо из координат конечной точки вычесть координаты начальной. Для рассмотренного примера с точками A (1, 5); B (3, 2) координаты вектора будут: AB = (2 — 1); (3 — 5). То есть справедливо будет записать: AB (1; -2). Для общего случая можно сказать, что формула координаты вектора по двум точкам имеет следующий вид: AB (x2 — x1, y2 − y1), где икс и игрек один — положение первой точки, а икс и игрек два — второй.

Это выражение справедливо не только для плоскости, но и для нахождения координат в пространстве. В этом случае добавляется третья осью. Обозначается она часто буквой Z. Соответственно, каждая точка будет описываться уже не двумя координатными значениями, а тремя — по числу осей: A (x1, y1, z1) и B (x2, y2, z2). Отсюда следует, что координаты вектора определяются уже по формуле: AB = (x2 — x1; y2 — y1; z2 — z1).

При сложении, умножении, вычитании двух ограниченных линий нужно выполнять поэлементно действия над их координатами. Например, AB (x 1, y 1) + BC (x 2, y 2) = AC (x 1 + x 2, y 1 + y 2).

Видео:Как найти координаты вектора?Скачать

Примеры решения задач

В своём большинстве задачи на поиск длины вектора по координатам или просто вычисление расположения отрезка в плоскости не представляет труда. Но эти действия нужно уметь выполнять, так как проекции очень часто используются при рассмотрении различных физических процессов.

Есть типовые задачи, дающиеся в седьмом классе средней школы для самостоятельной работы. Проработав их и научившись находить ответ, можно будет утверждать о знании темы. Вот один из вариантов примеров разной сложности:

В пространстве расположены две точки. Одна из них имеет координаты А (4, -3, 2), а другая B (0, 4, -9). Определить значения отрезка, полученного соединением этих точек. Рассмотреть оба варианта направления. Для решения поставленной задачи нужно вспомнить правило и просто вычесть из вторых координат соответствующие им первые. Когда А является началом отрезка, получим: AB = (0 — 4; 4 + 3; 0 — 4) = (-4; 7; -4). Для второго случая координаты будут следующими: BA = (4 — 0; -3 — 4; 2 + 9) = (4; -7; 11). Пример решён.
Найти координаты точки C отрезка СK (3,1), если координаты второй точки K (1, -2). Алгоритм решения такого задания строится на обратном. Необходимо будет из величин, определяющих отрезок, вычесть значения первой точки. По отношению к оси ординаты: CKx = Kx — Cx; Cx = Kx — CKx = 1 — 3 = -2. Относительно оси абсциссы: CKy = Ky — Cy; Cy = Ky — CKy = -2 — 1 = -3. Получается, что точка С имеет координаты (-2, -3).

Вот задача посложнее. Имеются две точки на плоскости. Первая имеет координаты L (1, 5), а вторая J (2, 7). Нужно найти длину соединяющего их отрезка. Для наглядности можно нарисовать чертёж, на которой изобразить эти две точки и объединяющую их прямую. Затем из этих координат нужно провести два перпендикуляра, таким образом, чтобы они пересеклись. Место их пересечения нужно как-то обозначить. Пусть это будет буква T.

Посмотрев на рисунок, можно заметить, что полученная фигура есть не что иное, как прямоугольный треугольник. Получается, что отрезки LT и JT— это катеты. Поэтому нужно лишь найти их длины по модулю и применить теорему Пифагора. Осюда, длина: |LT| = x2 — x1 = 7 — 5 = 2, |JT| = 2 — 1 =1. Исходя из формулы для нахождения гипотенузы, искомая длина будет равняться: d = √ LT 2 + JT 2 = √ 2 2 + 1 2 = √5.

Таким образом, все задачи на нахождение длины или расположения отрезка решаются через формулу координат. При этом не имеет значения, какое пространство рассматривается. Она справедлива как к двухмерному, так и n-мерному.

Видео:№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать

Использование онлайн-калькулятора

На практике чаще всего решение задач подразумевает нахождение какого-либо параметра в пространстве. Особенно это характерно для физики при изучении электромагнетизма или движения. Нередко приходится на координатных осях откладывать точки, в итоге образующие сложную фигуру. Поэтому даже незначительная, на первый взгляд, ошибка приведёт к неправильному ответу.

Гораздо эффективнее использовать так называемые онлайн-калькуляторы. Это обычные сайты, содержащие специальные программы для расчёта математических заданий. Пользоваться ими сможет любой, у кого есть доступ к интернету и установленный веб-браузер. Всё что требуется от пользователя, это просто в предложенную форму ввести исходные данные и нажать интерактивную кнопку, часто подписанную «Вычислить». Приложение запустится автоматически и через несколько секунд выдаст ответ. При этом за его точность можно не переживать. Ведь в основе работы программы используются алгоритмы на основе математических формул.

Из наиболее популярных сервисов, предоставляющих бесплатный доступ к своим услугам, можно выделить следующие:

ru.onlinemschool;
ru.solverbook;
math.semestr;
geleot;
mathonline.um-razum.

Это сервисы доступны на русском языке, имеют простой и понятный интерфейс. Их услуги привлекательны как для инженеров, выполняющим сложные расчёты, так и учащихся. Для первых это экономия времени и точный результат, а для вторых — отличное подспорье в учёбе. Всё дело в том, что эти сайты на своих страницах содержат весь необходимый теоретический материал с примерами вычислений. Кроме того, программа не просто выдаёт расчёт, но и выводит на дисплей пошаговое решение с описанием ключевых моментов.

Таким образом, даже ничего не понимая, ученик, попробовав решить несколько заданий, научится самостоятельно вычислять ответ. Векторные формулы отлично поддаются автоматизированному вычислению. Поэтому часто есть резон решать задания по нахождению векторных координат на онлайн-калькуляторе.