Построить прямую проходящую через данную точку и параллельную данной прямой с помощью циркуля

Вы будете перенаправлены на Автор24

В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых.

Видео:Построение прямой, параллельной данной, через данную точку (Циркуль и Линейка)Скачать

Построение параллельных прямых с помощью циркуля и линейки

Рассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки.

Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой.

Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой.

На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой.

Рассмотрим этапы построения параллельной прямой:

1. Выберем произвольную точку на данной прямой и назовем ее $В$. обратим внимание, что выбор точки абсолютно произвольный, т.к. не влияет на результат построения.
2. С помощью циркуля и начертим окружность радиуса $АВ$ с центром в точке $В$.

На пересечении окружности и прямой отметим точку и назовем ее $С$.

С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения.

С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$.

Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$.

Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной.

Таким образом, получили параллельные прямые $ВС$ и $АD$:

$BC parallel AD$, т. $A in AD$.

На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки.

Готовые работы на аналогичную тему

Видео:Параллельные прямые циркулемСкачать

Построение параллельных прямых с помощью угольника и линейки

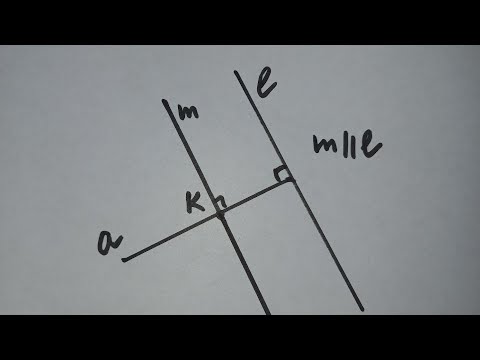
Для построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:

1. Угольник приложить к прямой $а$ диагональю (смотрите рисунок), а к его большему катету приложить линейку.
2. Передвинуть угольник по линейке до тех пор, пока данная точка $М$ не окажется на диагонали угольника.
3. Провести через точку $М$ искомую прямую $b$.

Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$:

$a parallel b$, т. $M in b$.

Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $alpha$ и $beta$.

Видео:Построение прямой, параллельной даннойСкачать

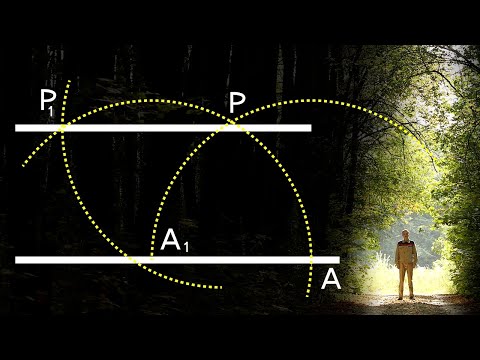
Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой

В случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником.

Пусть дана прямая $MN$ и расстояние $а$.

1. Отметим на заданной прямой $MN$ произвольную точку и назовем ее $В$.
2. Через точку $В$ проведем прямую, перпендикулярную к прямой $MN$, и назовем ее $АВ$.
3. На прямой $АВ$ от точки $В$ отложим отрезок $ВС=а$.
4. С помощью угольника и линейки проведем прямую $CD$ через точку $С$, которая и будет параллельной заданной прямой $АВ$.

Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$.

Видео:Построение прямой, параллельной даннойСкачать

Другие способы построения параллельных прямых

Еще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике.

При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2022

Видео:Перпендикуляр к прямой через заданную точку.Скачать

Как построить параллельные прямые через точку с помощью циркуля и линейки

Провести линию, проходящую через определенную точку и параллельную данной, можно легко с помощью циркуля. Приступим.

Сначала проводим первую прямую, ставим точку А.

Берем циркуль и ставим острием в любое место на линии. Отмеряем расстояние до точки А.

Проводим окружность так, чтобы она пересекла прямую в двух местах.

Если линия не дотягивает, тогда продлеваем ее.

Ставим циркуль в первое пересечение и отмеряем расстояние между ним и точкой А.

После ставим во втором месте пересечения и проводим окружность так, чтобы она пересекла прежнюю.

Берем линейку и через получившееся место пересечения и точку А проводим линию. Если все сделали аккуратно, прямая будет идеально параллельно первой.

Видео:Как построить прямую, перпендикулярную данной прямой через точку, которая лежит на данной прямойСкачать

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Видео:Построение прямой параллельной данной прямой проходящей через точку вне данной прямойСкачать

Построение отрезка, равного данному

Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Видео:Построение прямой, параллельной данной прямой через точку, не лежащей на ней (циркуль и линейка).Скачать

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Видео:КАК ПОСТРОИТЬ ПАРАЛЛЕЛЬНУЮ ПРЯМУЮ ЧЕРЕЗ ЗАДАННУЮ ТОЧКУ? Примеры | МАТЕМАТИКА 6 классСкачать

Построение угла, равного данному

Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Видео:Построение перпендикуляра к прямойСкачать

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Видео:ПОСТРОЕНИЕ ПРЯМОЙ ПЕРПЕНДИКУЛЯРНОЙ ДАННОЙ И ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ. ЗАДАЧИ. ГЕОМЕТРИЯ 7 классСкачать

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

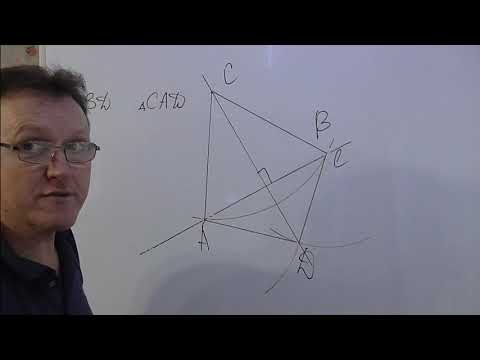
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Видео:Построить прямую параллельную даннойСкачать

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Видео:4K Как начертить параллельные прямые при помощи циркуля, how to draw parallel linesСкачать

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Видео:Как провести перпендикуляр в данную точку на прямой с помощью циркуляСкачать

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

🌟 Видео

Построение прямой параллельной данной. 6 класс.Скачать

Построение прямой, параллельной данной, через заданную точку - циркулемСкачать

Построить перпендикуляр к прямой из точки не принадлежащей этой прямой.Скачать

Построение прямой, перпендикулярной данной и проходящей через данную точкуСкачать

Построение перпендикуляраСкачать