Как найти длину медианы в треугольнике векторы

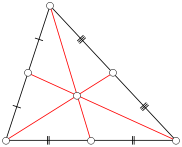
Как найти медиану если даны координаты вершин треугольника?

Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

1) Так как AF — медиана треугольника ABC, то F — середина BC.

Видео:Длина медианы треугольникаСкачать

Как найти медиану из векторов

Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Найти медиану треугольника по координатам вершин

Как найти медиану если даны координаты вершин треугольника?

Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

1) Так как AF — медиана треугольника ABC, то F — середина BC.

Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Как найти медиану вектора

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Применение векторов к решению задач

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Найти медиану треугольника по координатам вершин

Как найти медиану если даны координаты вершин треугольника?

Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

1) Так как AF — медиана треугольника ABC, то F — середина BC.

Видео:Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Вычислить медиану значений, хранящихся в Vector-c++?

Я студент-программист, и для проекта, над которым я работаю, из того, что мне нужно сделать, это вычислить медианное значение вектора значений int. Я должен сделать это, используя только функцию сортировки из STL и векторных функций-членов, таких как .begin() , .end() и .size() .

Я также должен убедиться, что нахожу медиану, имеет ли вектор нечетное число значений или четное число значений.

и я штука ниже я включил моя попытка. Так где же я ошибаюсь? Я был бы признателен, если бы вы дали мне несколько советов или ресурсов, чтобы двигаться в правильном направлении.

код:

спасибо!!

Видео:Уравнения стороны треугольника и медианыСкачать

6 ответов

Вы делаете дополнительное разделение и в целом делаете его немного более сложным, чем это должно быть. Кроме того, нет необходимости создавать делитель, когда 2 на самом деле более значим в контексте.

нет необходимости полностью сортировать вектор: std::nth_element может сделать достаточно работы, чтобы поставить медиану в правильное положение. См. мой ответ на этот вопрос для примера.

конечно, это не поможет, если ваш учитель запрещает использовать правильный инструмент для работы.

следующая простая функция, которая возвращает медиану набора значений с помощью итераторов ввода. Он не будет изменять исходный набор данных за счет выделения памяти.

Если вы хотите избежать затрат на выделение копии набора данных и хотите изменить базовый набор данных, вы можете использовать это вместо:

не делай этого. Это просто делает ваш код более запутанным. Вы, вероятно, читали рекомендации о том, чтобы не использовать магические числа, но четность против странности чисел является фундаментальным свойством, поэтому абстрагирование этого не дает никакой пользы, но затрудняет читаемость.

вы берете итератор в конец вектора, беря другой итератор, который указывает на один конец вектора, добавляя итераторы вместе (что не является операцией, которая имеет смысл), и затем делим полученный итератор (что также не имеет смысла). Это более сложный случай; сначала я объясню, что делать с вектором нечетного размера, а четный случай оставлю вам в качестве упражнения.

опять же, вы делите итератор. Вместо этого вы хотите увеличить итератор до начала вектора на hWScores.size() / 2 элементы:

и обратите внимание, что вы должны разыменования итераторы для получения значений из них. Было бы проще, если бы вы использовали индексы:

я приведу ниже пример программы, которая несколько похожа на ту, что в ответе Макса С. Чтобы помочь ОП продвигать свои знания и понимание, я внес ряд изменений. У меня:

a) изменил вызов по ссылке const на вызов по значению, так как сортировка захочет изменить порядок элементов в вашем векторе (EDIT: я только что видел, что Роб Кеннеди также сказал это, когда я готовил свой пост)

b) заменил size_t на более подходящий вектор >:: size_type (собственно, удобный синоним последнего),

c) сохраненный размер / 2 в промежуточную переменную,

d) выбрасывается исключение, если вектор пуст, и

e) я также ввел условный оператор (? :).

На самом деле, все эти исправления прямо из главы 4 «ускоренного C++» Кенига и Му.

Я не совсем уверен, каковы ваши ограничения на пользователя функций-членов vector, но индексируйте доступ с [] или at() упростит доступ к элементам:

вы также можете работать с итераторами типа begin() + offset как вы сейчас делаете, но затем вам нужно сначала вычислить правильное смещение с size()/2 и добавить, что до begin() , а не наоборот. Также вам нужно разыменовать результирующий итератор, чтобы получить доступ к фактическому значению при этом точка:

Видео:Построение медианы в треугольникеСкачать

Применение векторов к решению задач

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

Видео:Вычисляем высоту через координаты вершин 1Скачать

Длина медианы треугольника

Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.

Видео:Три точки заданы координатами Найти длину медианы треугольникаСкачать

Калькулятор длины медианы треугольника

Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника

Формула расчета длины медианы

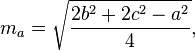
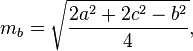
• a,b,c — Длина сторон треугольника.

Пример расчета медиан:

Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.

Получаем:

A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )

Решение:

Шаг 1:

Найдем длину сторон a,b,c используя формулу

Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )

a = √((5 — 8) 2 + (6 — 9) 2 )= 4.242

Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )

b = √((1 — 5) 2 + (5 — 6) 2) = 4.123

Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )

c = √((8 — 1) 2 + (9 — 5) 2) = 8.062

Шаг 2:

Полученные значения a,b,c применяем в формулы

m_a = (1/2) √2c 2 + 2b 2 — a 2

m_b = (1/2) √(2c 2 + 2a 2 — b 2 )

m_c = (1/2) √(2a 2 + 2b 2 — c 2 )

• m_a = (1/2)√(2(8.062) 2 + 2(4.123) 2 — 4.242 2 )= 6.042
• m_b = (1/2)√(2(8.062) 2 + 2(4.242) 2 — 4.123 2 )= 6.103
• m_c = (1/2)√2(4.242) 2 + 2(4.123) 2 — 8.062 2 = 1.118

🔍 Видео

Вычисление медианы, высоты и угла по координатам вершинСкачать

Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Формулы для медианы треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Нахождение длины вектора. Практическая часть. 9 класс.Скачать

длина медианы #shortsСкачать

Как найти медиану, зная стороны треугольника? Удвоение медианы.Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Площадь треугольника, построенного на векторахСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать