Дан четырехугольник abcd середины противоположных сторон которого пересекаются в точке к докажите

Условие

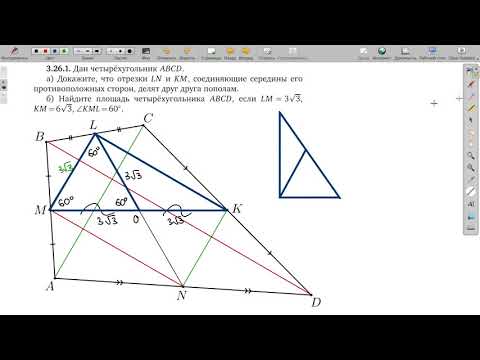
Дан четырехугольник ABCD.
а) Докажите, что отрезки LN и KM, соединяющие середины его противоположных сторон, делят друг друга пополам.
б) Найдите площадь четырехугольника ABCD, если LM=3sqrt(3), KM=6sqrt(3), угол KML=60 градусов.

Решение

Ответ: 54sqrt(3)

Почему треугольник KLM прямоугольный?

потому что сумма квадратов двух его сторон (катетов) равна квадрату третей (гипотенузе), а этому свойству удовлетворяет только прямоугольный треугольник

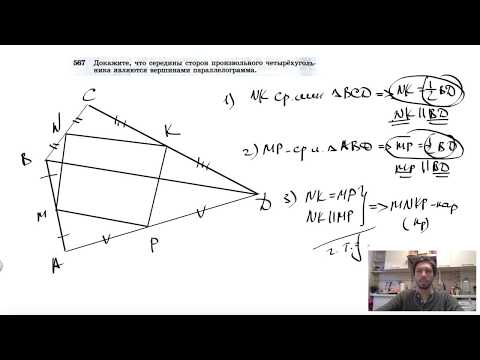
Видео:№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать

VIII.3. Задачи к теоретической карте № 8

№1. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны. Доказать.

План доказательства.

1. Параллелограмм MNPK – ромб.

Используемые факты из теоретической карты: 1.1.

№2. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6 см. Длина отрезка, соединяющего середины оснований равна 4,5 см. Найти площадь трапеции.

Дополнительные построения:

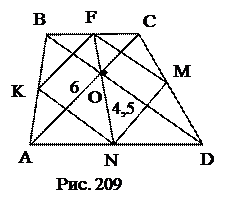
KFMN – параллелограмм, вершины

которого – середины сторон трапеции.

1. KFMN – прямоугольник.

Ответ: см. Используемые факты из теоретической карты: 1.1; 1.2.

№3. Доказать, что отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

О – точка пересечения отрезков, соединяющих середины противоположных сторон четырехугольника ABCD (рис. 210.1). L – середина диагонали АС, F- середина диагонали BD (рис. 210.2).

1. О – середина NK. 2. NLKF – параллелограмм. 3. О – середина NK и LF.

Используемые факты из теоретической карты: 1.1.

№4. Найти площадь параллелограмма, если длины его сторон равны a и b, а угол между диагоналями, противолежащий стороне длины а, равен .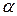

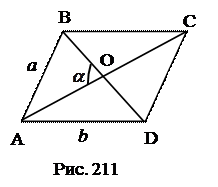
План решения.

1. Выразить а 2 через АО и ОВ.

2. Выразить b 2 через АО и OD.

3. Выразить из (1) и (2) АО∙ОВ и АС∙BD.

Ответ: .

Используемые факты из теоретической карты: 2.

№5. Сумма диагоналей ромба равна m, а его площадь S. Найти сторону ромба.

План решения.

1. Выразить m 2 через АС и BD.

2. Выразить АС∙ BD через S.

3. Выразить АС 2 + BD 2 через m и S.

4. Выразить АО 2 +ОВ 2 через m и S.

Ответ:

Используемые факты из теоретической карты: 2.

№6.В ромб с острым углом 60°вписан четырёхугольник так, что его вершинами являются основания высот, проведённых из точки пересечения диагоналей ромба к его сторонам, Найти отношение площади четырёхугольника к площади ромба.

План решения.

Пусть сторона ромба равна а.

1. Выразить NQ через а.

2. Выразить S_MNPQ через NQ, а затем через а.

3. Выразить S_ABCD через а.

4. Hайти искомое отношение.

Используемые факты из теоретической карты: 2.

№7.Доказать,что площадь треугольника равна произведения двух медиан на синус угла между ними.

План доказательства.

1. Выразить площадь треугольника ВС₁А₁

через площадь данного треугольника S.

2. Выразить площадь четырехугольника

3. Выразить площадь данного треугольника

через площадь четырехугольника АС₁А₁С

и площадь треугольника ВС₁А₁.

Используемые факты из теоретической карты: 2.

№8. Диагональ трапеции вписанной в круг радиуса R, образует с ее боковыми сторонами углы и . Найти площадь трапеции.

План решения.

6. АС (по теореме синусов ∆ACD).

Ответ: .

Используемые факты из теоретической карты: 2.

№9. Четырехугольник разделен диагоналями на четыре треугольника. Наименьшие площади трех из них равны 10, 20 и 30. Найти площадь данного четырехугольника.

План решения.

1. Установить соответствие между треугольниками и площадями.

2. Найти площадь четвертого треугольника.

Используемые факты из теоретической карты: 3.

№10. В трапеции ABCD(AВ||CD). О – точка пересечения диагоналей АС и BD. Площади треугольников АВО и CDO равны соответственно 10 и 40. Найти
площадь трапеции.

План решения.

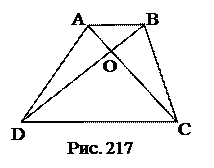
Используемые факты из теоретической карты: 3.

№11. Площадь трапеции равна 3, основания относятся как 1:2. Найдите площади треугольников, на которые трапеция разделена диагоналями.

План решения.

4. 2S₁+ S₁+2S₁=3. 5. S₁, S₂, S₃, S₄.

Ответ:

Используемые факты из теоретической карты: 3.

№12. В равнобокую трапецию вписана окружность радиуса 2. Найти площадь трапеции, если длина боковой стороны равна 10.

План решения.

Используемые факты из теоретической карты: 4,5.

№13. Около окружности, радиус которой равен 1,2 см описан четырехугольник ABCD, у которого АВ=3 см, ВС=2 см, AD=4 см. Найти площадь этого четырехугольника.

План решения.

Используемые факты из теоретической карты: 5, 4.

№14. Около круга описана равнобедренная трапеция, площадь которой равна 32 см 2 . Найти стороны трапеции, если угол при большем основании равен 30 0 .

План решения.

1. Выразить ВС+AD, ВF, S_ABCD через АВ.

2. АВ. 3. AD+BC. 4. AF. 5. BC, AD.

Ответ: 8 см, см, см, 8 см.

Используемые факты из теоретической карты: 5.

№15. Равнобедренная трапеция ABCD (AD||BC, AD>BC) описана около окружности с центром О. О₁ – точка пересечения диагоналей трапеции. Площади треугольников АО₁В и АОВ равны 3 и 4. Найти углы трапеции.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

1. АВ∙r. 2. Выразить полупериметр ABCD через АВ. 3. S_ABCD.

4. Составить систему уравнений (Рис. 222.2).

5. S₂, S₄. 6. AD: ВС. 7. Выразить AD через ВС. 8. Выразить АК через ВС.

9. Выразить АВ через ВС. 10. АК:АВ=cos

Ответ: 60 0 , 120 0 .

Используемые факты из теоретической карты: 3, 4, 5.

№ 16. В четырехугольнике проведены все биссектрисы внутренних углов. Доказать, что пересечением биссектрис образовался четырехугольник, около которого можно описать окружность.

План доказательства.

1. ÐВВ₁С выразить через ÐВ иÐС четырехугольникаABCD.

2. ÐАD₁D выразить через ÐA иÐD четырехугольникаABCD.

Используемые факты из теоретической карты: 6.

№17. Из точки М, лежащей вне окружности, проведены два луча, пересекающие окружность в точках А, В, С и D. Доказать, что треугольники АМС и DMB подобны.

1. .

2. .

3. .

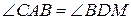
Используемые факты из теоретической карты: 6.

№18. Через середину С дуги АВ проведены прямые CD и CE, пересекающие хорду АВ в точках H и F. Доказать, что около четырехугольника DHFE можно описать окружность.

План решения.

1.

2. .

3. .

Используемые факты из теоретической карты: 6.

№19. Через вершину С треугольника АВС проведены его внутренняя биссектриса CD и внешняя биссектриса. Из вершины В проведен перпендикуляр к стороне АВ, пересекающий внешнюю биссектрису в точке К. Доказать, что около четырехугольника CDBK можно описать окружность (точка D лежит на стороне АВ)

План доказательства.

CD – биссектриса внутреннего угла АСВ,

СК – биссектриса внешнего угла DCB.

2. ÐDCK+ÐDBK=180 0 .

Используемые факты из теоретической карты: 6.

IX. ТРАПЕЦИЯ И ПАРАЛЛЕЛОГРАММ

Видео:№808* Точки А и С — середины противоположных сторон произвольного четырехугольника, а точки B и DСкачать

Дан вписанный четырёхугольник ABCD продолжения его противоположных сторон пересекаются в точках P и Q пусть K и N — середины диагоналей докажите что сумма углов pkq и pnq равна 180 градусов?

Математика | 10 — 11 классы

Дан вписанный четырёхугольник ABCD продолжения его противоположных сторон пересекаются в точках P и Q пусть K и N — середины диагоналей докажите что сумма углов pkq и pnq равна 180 градусов.

получившиеся треугольники AOD и АО1В.

Они подобны по первому признаку

подобия : два угла одного треуг — ка соответственно равны двум углам

&lt ; AOD = &lt ; AO1B = 20° по условию ;

Значит, &lt ; ADO = &lt ; ABO1 (это углы B и D в четырехугольнике)

общий для обоих треугольников AOD и АО1В угол А будет х.

неизвестные углы ADO и ABO1, зная, что сумма углов треугольника равна

&lt ; ADO = &lt ; ABO1 = 180 — (&lt ; A + 20) = 160 — &lt ; A = 160 — x (&lt ; D = &lt ; B = 160 — x)

Рассмотрим четырехугольник ABCD.

Зная сумму его углов, выразим угол С : &lt ; C = 360 — (&lt ; A + &lt ; B + &lt ; D) = 360 — (x + 160 — x + 160 — x) = 40 + х.

&lt ; C = 40 + &lt ; A (поскольку за х мы принимали угол А).

Таким образом, мы видим, что разница между углами С и А равна 40 градусов.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Сторона СD параллелограмма ABCD вдвое больше стороны ВС?

Сторона СD параллелограмма ABCD вдвое больше стороны ВС.

Точка F — середина стороны CD.

Докажите что, BF — биссектриса угла ABC.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Биссектрисы углов B и CБиссектрисы углов B и C параллелограмма ABCD пересекаются в точке M стороны AD?

Биссектрисы углов B и CБиссектрисы углов B и C параллелограмма ABCD пересекаются в точке M стороны AD.

Докажите, что M — середина AD.

Видео:№432. Точки М и N — середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямыеСкачать

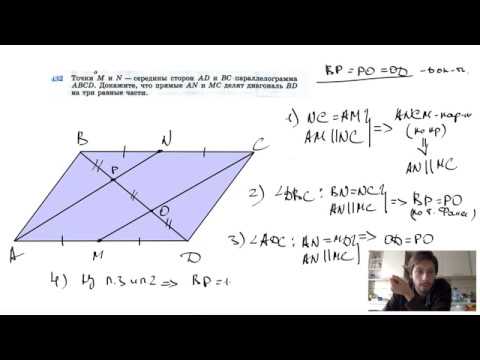
Биссектрисы углов C и D?

Биссектрисы углов C и D.

Биссектрисы углов C и D параллелограмма ABCD пересекаютсяв точке К стороны АВ.

Докажите, что К — середина АВ.

Видео:Доказать, что точки лежат на одной окружностиСкачать

Точка Е середина стороны BC параллелограмма ABCD?

Точка Е середина стороны BC параллелограмма ABCD.

Отрезок АЕ пересекает диагональ BD в точке F.

Докажите подобие треугольников AFD и EFB.

Видео:ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать

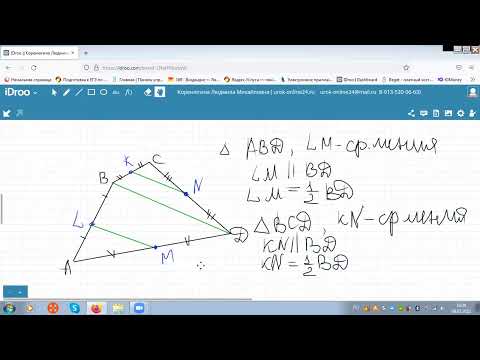
Биссектрисы углов а и в параллелограмма авсд пересекаются в точке f стороны СД?

Биссектрисы углов а и в параллелограмма авсд пересекаются в точке f стороны СД.

Докажите, что F — середина СД.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Биссектриса прямого угла трапеции пересекает боковую сторону в её середине?

Биссектриса прямого угла трапеции пересекает боковую сторону в её середине.

Докажите, что меньшая боковая сторона равна сумме оснований.

Видео:Биссектрисы пересекаются в одной точке| Задачи 28-33 | Решение задач | Волчкевич|Уроки геометрии 7-8Скачать

Биссектриса прямого угла трапеции пересекает боковую сторону в её середине?

Биссектриса прямого угла трапеции пересекает боковую сторону в её середине.

Докажите, что меньшая боковая сторона равна сумме оснований.

Видео:3.26.1. Планиметрия. Гордин Р.К.Скачать

Установите правильное соответствие?

Установите правильное соответствие.

1) Четырёхугольник, диагонали которого делят его на четыре равных равнобедренных треугольника.

2) Четырёхугольник, противоположные стороны которого попарно равны, и одна из диагоналей является биссектрисой его угла.

3) Четырёхугольник, диагональ которого равна и точкой пересечения делятся пополам.

4)Четырёхугольник, вершины которого является середина ми сторон произвольного четырёхугольника.

5) Четырёхугольник, две противоположные стороны которого пересекаются некоторой прямой под прямым углом.

6) Четырёхугольник, имеющий две пары смежных равных сторон.

Видео:12-ти ЧАСОВОЙ СТРИМ ПО №16 из ЕГЭ по математикеСкачать

Иссектрисы углов A и D параллелограмма abcd пересекаются в точке K , лежащей на стороне BC ?

Иссектрисы углов A и D параллелограмма abcd пересекаются в точке K , лежащей на стороне BC .

Докажите, что K — середина BC .

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N , лежащей на стороне CD ?

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N , лежащей на стороне CD .

Докажите, что N — середина CD .

Если вам необходимо получить ответ на вопрос Дан вписанный четырёхугольник ABCD продолжения его противоположных сторон пересекаются в точках P и Q пусть K и N — середины диагоналей докажите что сумма углов pkq и pnq равна 180 градусов?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

💥 Видео

8 класс, 4 урок, ПараллелограммСкачать

№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

ВСЕ правила и формулы ПЛАНИМЕТРИИСкачать

Параллелограмм. 8 класс.Скачать

№129. Отрезки АС и BD пересекаются в середине О отрезка AC, ∠BCO = ∠DAO. Докажите, что ΔВОА=ΔDОС.Скачать

ОГЭ Задания 24 и 25. Все про четырехугольникиСкачать

Геометрия Точки M, N, K и P – середины сторон AB, BC, CD и AD параллелограмма ABCD соответственноСкачать

Решение задач пространственный четырехугольникСкачать