Как доказать что четырехугольник квадрат

Видео:№1080. Докажите, что любой правильный четырехугольник является квадратом.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Квадрат, его свойства и признаки.

Определение. Квадратом называется прямоугольник, у которого все стороны равны.

Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:

Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.

Квадратом называется параллелограмм, у которого все стороны и углы равны.

Квадратом называется ромб, у которого все углы прямые.

Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.

У квадрата диагонали пересекаются и точкой пересечения делятся пополам.

У квадрата диагонали взаимно перпендикулярны.

У квадрата диагонали являются биссектрисами его углов.

У квадрата диагонали равны.

У квадрата стороны являются высотами.

Каждая диагональ квадрата делит его на равные прямоугольные треугольники.

Теперь определим признаки квадрата.

ТЕОРЕМА ( I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.

Так как – прямоугольник, то у него противолежащие стороны равны.

– квадрат (по определению), ч.т.д.

ТЕОРЕМА ( II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.

по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).

– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку квадрата, прямоугольник является квадратом, ч.т.д.

ТЕОРЕМА ( III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Так как – биссектриса , то .

по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку квадрата, прямоугольник является квадратом, ч.т.д.

ТЕОРЕМА ( IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.

по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е. . Эти углы являются внутренними односторонними при параллельных прямых и , следовательно, их сумма равна , т.е. , а, значит, и . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по . Значит, такой ромб является квадратом, ч.т.д.

ТЕОРЕМА ( V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.

Так как , то по II признаку ромба, параллелограмм является ромбом.

Так как , то по IV признаку квадрата, ромб является квадратом, ч.т.д.

ТЕОРЕМА ( VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.

1. Так как , то четырёхугольник является параллелограммом (по признаку параллелограмма).

2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.

ТЕОРЕМА ( VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.

1. Так как , то четырёхугольник является ромбом (по V признаку ромба).

2. Так как , то ромб, который по определению является параллелограммом, является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.

3. Итак, прямоугольник , у которого все стороны равны, является квадратом (по определению), ч.т.д.

Если в прямоугольнике две его смежные стороны равны, то он является квадратом.

Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.

Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Если в ромбе диагонали равны, то этот ромб является квадратом.

Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.

Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.

Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.

Периметр квадрата равен см. Найдите сторону квадрата .

На рисунке четырёхугольник – квадрат, . Докажите, что выпуклый четырёхугольник также является квадратом.

На рисунке четырёхугольник – прямоугольник, . Докажите, что выпуклый четырёхугольник является квадратом.

В треугольнике . На сторонах и взяты точки и , а на стороне – точки и так, что четырёхугольник является квадратом, . Найдите .

В треугольнике . На сторонах отмечены точки соответственно так, что четырёхугольник является квадратом, . Найдите .

На сторонах и квадрата отмечены точки и соответственно, . Отрезки и пересекаются в точке . Найдите .

На сторонах квадрата отмечены соответственно точки . Сравните отрезки и .

На катетах и прямоугольного треугольника построены квадраты и . Докажите, что сумма расстояний от точек и до прямой равна .

На катетах и прямоугольного треугольника построены квадраты и . Прямые и пересекаются в точке . Докажите, что .

Длина проекции одной из сторон квадрата на его диагональ равна . Найдите длину диагонали.

В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.

Дан квадрат . Докажите, что – квадрат.

Дан квадрат . Докажите, что – ромб.

Дан квадрат . На стороне взята точка такая, что . Докажите, что точки – вершины равнобедренного треугольника.

Дан квадрат . Точки – середины его сторон соответственно. Докажите, что .

Дан квадрат . Точки и делят его стороны и так, что . Докажите, что .

Квадраты и имеют общую вершину . Докажите, что медиана треугольника перпендикулярна отрезку .

Внутри квадрата взята точка так, что . Докажите, что треугольник равносторонний.

На рисунке – квадрат, точка принадлежит , точка принадлежит , точка принадлежит , прямые и пересекаются в точке . Докажите, что .

В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.

В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.

В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно см. Найдите периметр этого квадрата.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.

Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.

Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

На сторонах и квадрата отмечены точки и соответственно так, что . Определите взаимное расположение прямых и .

В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий угол . Найдите периметр квадрата, если катет треугольника равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.

Через точку – точку пересечения диагоналей квадрата проведена прямая, параллельная стороне и пересекающая стороны и в точках и соответственно. Найдите периметр квадрата, если известно, что .

Найдите периметр квадрата по данным на рисунке.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Параллелограмм: свойства и признаки

О чем эта статья:

Видео:ОГЭ Задание 25 Доказать что четырехугольник квадратСкачать

Определение параллелограмма

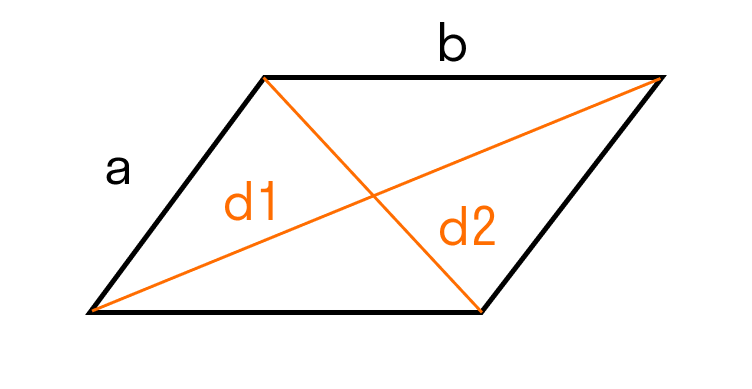
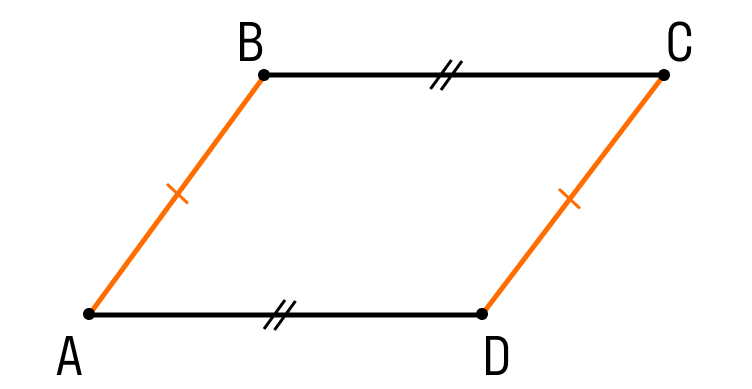
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

1. В параллелограмме точка пересечения диагоналей делит их пополам.
2. Любая диагональ параллелограмма делит его на два равных треугольника.
3. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.

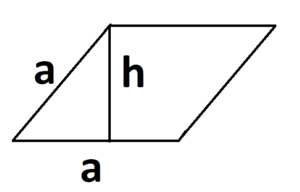
Как найти площадь параллелограмма:

1. S = a × h, где a — сторона, h — высота.
   
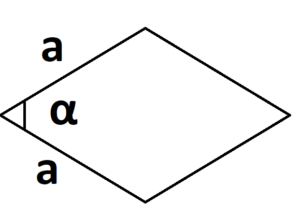
2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
   
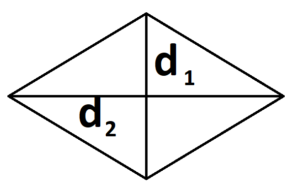
3. Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
   Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
   

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

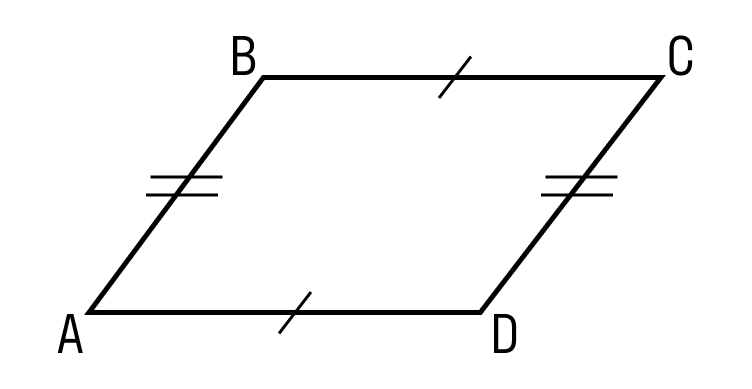
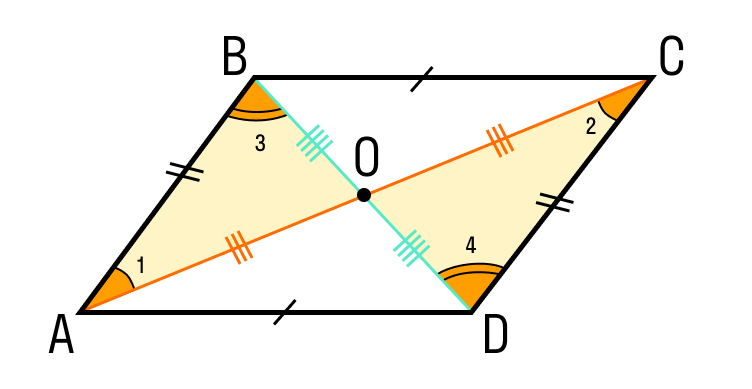
1. Противоположные стороны параллелограмма равны.
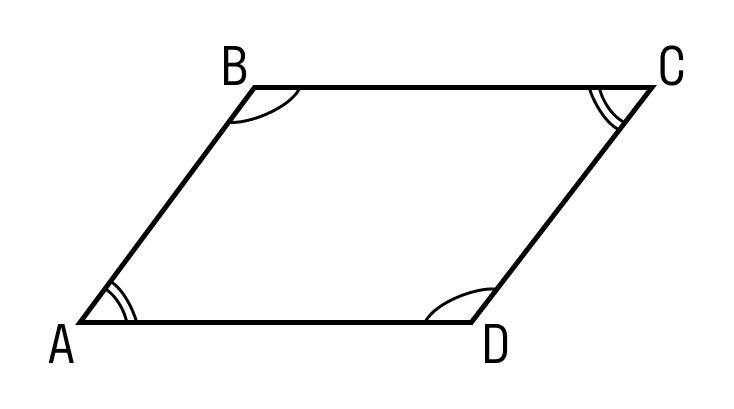
   ABCD — параллелограмм, значит, AB = DC, BC = AD.
   
2. Противоположные углы параллелограмма равны.
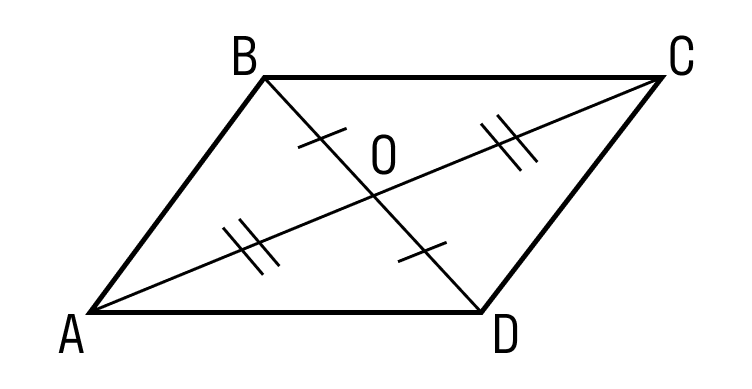
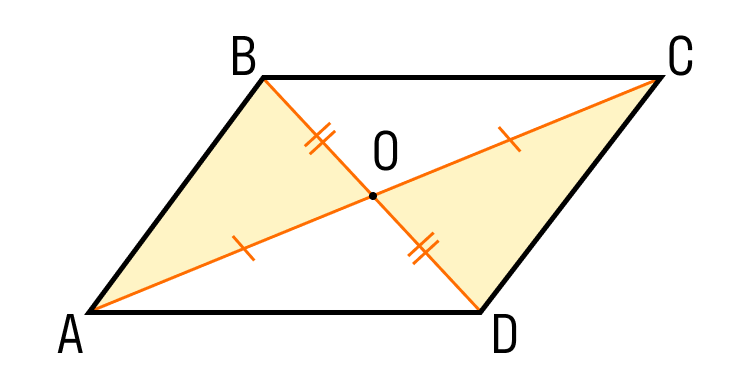
   ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
   
3. Диагонали параллелограмма точкой пересечения делятся пополам.
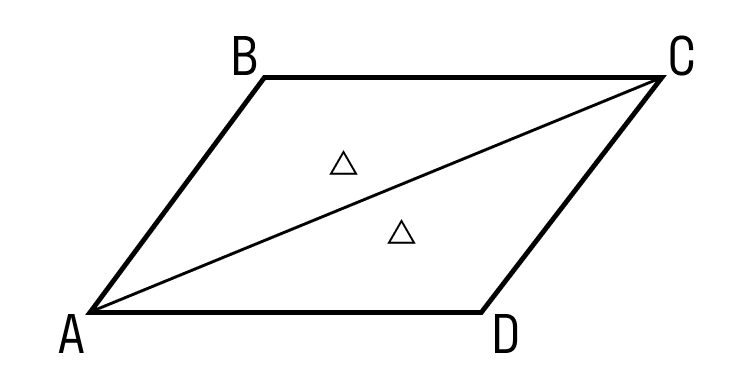
   ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
   
4. Диагональ делит параллелограмм на два равных треугольника.
   ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
   
5. Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
   ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
   
6. В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
   

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

1. AB = CD как противоположные стороны параллелограмма.
2. ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
3. Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
   • CO = AO
   • BO = DO

   

Теорема доказана. Наше предположение верно.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

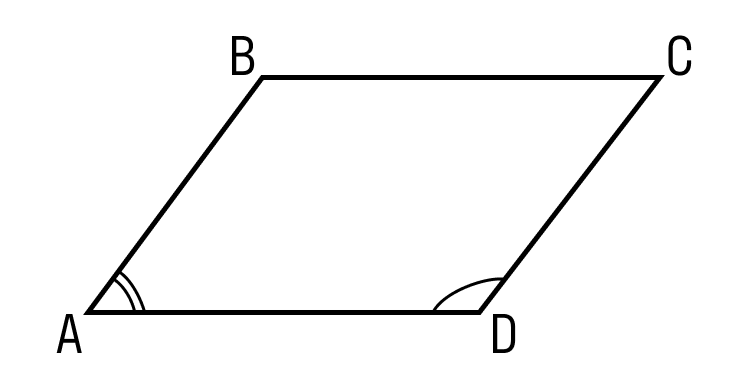
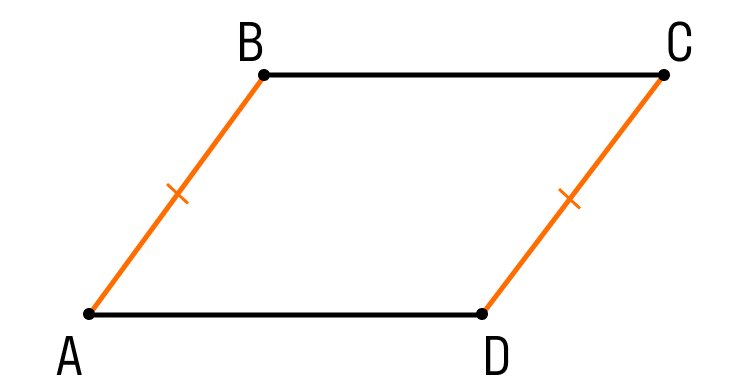
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB || CD
• AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

1. AC — общая сторона;
2. По условию AB = CD;
3. ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

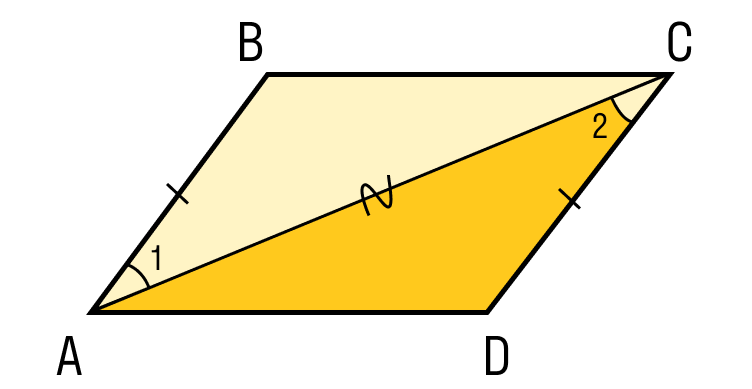
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB = CD
• BC = AD

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

• AC — общая сторона;
• AB = CD по условию;
• BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

• CO = OA;
• DO = BO;
• углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Какой четырехугольник называется квадратом, а какой прямоугольником. Какой четырехугольник называется трапецией

Четырехугольники, как частный случай многоугольников, очень важная тема, изучаемая в школьном курсе геометрии. Современная программа подразумевает ознакомление с этим материалом в восьмом классе. В рамках школьного обучения рассматриваются исключительно выпуклые четырехугольники. Остальные же изучаются на уровне высших учебных заведений.

Изучение четырехугольников происходит в разных программах изучения геометрии неодинаково. Порядок введения понятия зависит от последовательности подачи материала о многоугольниках.

Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Порядок изучения четырехугольников

Вам будет интересно: Формула решения квадратных уравнений и примеры ее использования

В одном случае четырехугольник рассматривается как частный случай многоугольника, в другом — определяется как совокупность отрезков и точек, расположенных на их пересечении, числом по четыре. При этом должны выполняться условия непринадлежности любых из трех этих точек одной прямой, и отсутствия пересечений, кроме как в вершинах.

В большинстве школ Четырехугольники изучаются в восьмом классе. Изучив сначала параллельность прямых, затем теорему о сумме углов многоугольника, переходят к параллелограмму. Рассмотрев его признаки и доказав связанные с ними теоремы, переходят к остальным частным случаям, получая ответы на вопросы: какой четырехугольник называется квадратом, ромбом, прямоугольником и различными видами трапеций.

Вам будет интересно: Какова площадь земного шара?

Еще один подход — изучение четырехугольников при рассмотрении темы подобных фигур. Здесь также последовательно изучаются четырехугольники начиная с параллелограмма. Определяется – какой четырехугольник называется прямоугольником, трапецией. И конечно, подробно рассматривается, какими фигурами могут быть остальные четырехугольники.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Классификация фигур с четырьмя углами

Какой четырехугольник называется квадратом? Выяснить это можно, изучив все фигуры, имеющие отношения к данной по порядку. Первым в наше внимание попадет объект, называемый параллелограммом. Он образуется четырьмя прямыми попарно параллельными и пересекающимися. Отдельно определяются случаи, когда это происходит под углами в девяносто градусов и те, в которых все отрезки, образованные таким пересечениями, имеют одну длину. В завершение, выясним, какой четырехугольник называется трапецией.

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Четырехугольники, называемые выпуклыми

Остановимся на понятиях выпуклых, а также невыпуклых четырехугольников. Данное различие имеет большое значение, так как в школьной программе изучаются только первые из них.

Какой четырехугольник называется выпуклым? Для того чтобы разобраться в этом последовательно, проведем через все стороны фигуры прямые линии. Если во всех случаях весь четырехугольник лежит в одной из двух полуплоскостей образованных этой прямой – он выпуклый. В противном случае, соответственно, невыпуклый.

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Обычный параллелограмм

Теперь рассмотрим основные виды выпуклых четырехугольников. Начнем с параллелограмма. Выше мы приводили определение этой фигуры. Кроме определения стоит отметить несколько свойств этого выпуклого многоугольника.

Стороны параллелограмма, находящиеся напротив друг друга равны. Также равны друг другу и противоположные углы.

Пересечение отрезков, называемых диагоналями, образует угол в девяносто градусов. Если просуммировать квадраты их длин, то они составят сумму квадратов граней фигуры. Каждый такой отрезок образует два одинаковых треугольника и четыре равновеликих.

Любые два соседних угла при сложении дадут сто восемьдесят градусов.

При констатации факта, что геометрическая фигура обладает данными свойствами, можно утверждать, что она — параллелограмм. Таким образом, мы получим признаки этого четырехугольника, определяющие принадлежность фигуры именно к этому классу.

Площадь можно найти двумя способами. Первым будет являться поиск произведения синуса угла и длин, прилежащих к нему сторон. Второй способ — определение результата перемножения длин высоты и лежащей напротив нее грани.

Какой четырехугольник называется ромбом? Такой, у которого все из образовывающих его сторон равняются между собой. Эта геометрическая фигура обладает всеми свойствами и признаками параллелограмма. Еще одним свойством является факт, что в эту фигуру всегда вписывается окружность.

Параллелограмм, соседние стороны которого равны, однозначно определяется, как ромб. Площадь можно вычислить, как произведение квадрата стороны на синус одного из углов.

Видео:Задание 25 Доказать, что четырёхугольник прямоугольник Определение прямоугольникаСкачать

Прямоугольник

Какой четырехугольник называется прямоугольником? Такой, который обладает углами в девяносто градусов. Так как он тоже является параллелограммом, на него распространяются свойства и признаки этого четырехугольника. Также о прямоугольнике можно сказать следующее:

• Диагонали этой фигуры имеют одинаковую длину.
• Площадь определяется путем умножения сторон друг на друга.
• В случае, когда угол параллелограмма составляет девяносто градусов – можно утверждать, что это прямоугольник.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Квадрат

Следующий вопрос из тех, что мы рассмотрим в этой публикации, – какой четырехугольник называется квадратом? Это фигура, обладающая равными сторонами и углами в девяносто градусов. Исходя из указанных выше параметров, она обладает всеми теми же свойствами, которыми обладают прямоугольник и ромб. Соответственно имеет также их признаки.

К особенностям квадрата можно отнести уникальные свойства линий, соединяющих его противоположные вершины и называемых диагоналями. Они имеют одну длину и пересекаются под прямым углом.

Прикладное значение квадрата сложно переоценить. Благодаря своей универсальности, простоте определения площади и размеров, эта фигура широко используется в качестве эталонной меры. Число возведенное во вторую степень устойчиво называется математиками квадратом. С помощью квадратных единиц измеряют площадь, осуществляют интеграцию и общие приближения размеров на плоскости. Широко эта геометрическая концепция используется в архитектуре и ландшафтном дизайне.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Трапеция

Далее следует рассмотреть какой четырехугольник называется трапецией. Это будет фигура, имеющая расположенные параллельно друг другу стороны, называемые основаниями и непараллельные стороны, определяемые боковыми. Она образована четырьмя гранями и таким же количеством углов. Когда эти непараллельные отрезки равны, трапецию определяют как равнобокую. В случае, если у фигуры угол равен девяносто градусов, она будет считаться прямоугольной.

Такой четырехугольник, какой называется трапецией имеет еще один особый элемент. Линию, которая соединяет центры боковых сторон, называют средней. Длину ее можно определить, отыскав одну вторую результата сложения длин сторон, определяемых, как основания фигуры.

У равнобедренной трапеции так же, как и у равнобедренного треугольника, длины диагонали и углы между боковыми сторонами и основаниям равны.

Вокруг такой трапеции всегда возможно описание окружности.

Вписывается окружность в такую фигуру, сумма длин боковых сторон которой одинакова с результатом сложения ее оснований.

Видео:Короткие загадки, которые осилит не каждый профессорСкачать

Общие выводы по теме

В заключение можно сказать что в курсе геометрии достаточно доступно и подробно рассмотрен вопрос о том, какой четырехугольник называется квадратом. Несмотря на то, что в разных учебниках мы можем встретить некоторые отличия в последовательности изложения обозначенных выше тем, все они исчерпывающе освещают тему четырехугольников.

💥 Видео

3 правила для вписанного четырехугольника #shortsСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Прямоугольник. 8 класс.Скачать

Докажите, что это квадратСкачать

Квадрат. 8 класс.Скачать

Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать