Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
- Правильно — векторы
- Сложение
- Интуитивное изображение сложения
- Вычитание
- Длина вектора
- Умножение и деление вектора на число
- Да вроде несложно!
- Что дальше
- Делить вектор на число онлайн
- Калькулятор
- Инструкция
- Что такое деление вектора на число
- Векторы на ЕГЭ по математике. Действия над векторами
- Сложение векторов
- Вычитание векторов
- Умножение вектора на число
- Скалярное произведение векторов
- Онлайн-курс «Математика 10+11 100 баллов»
- 🎥 Видео
Видео:Умножение вектора на число. 9 класс.Скачать

Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
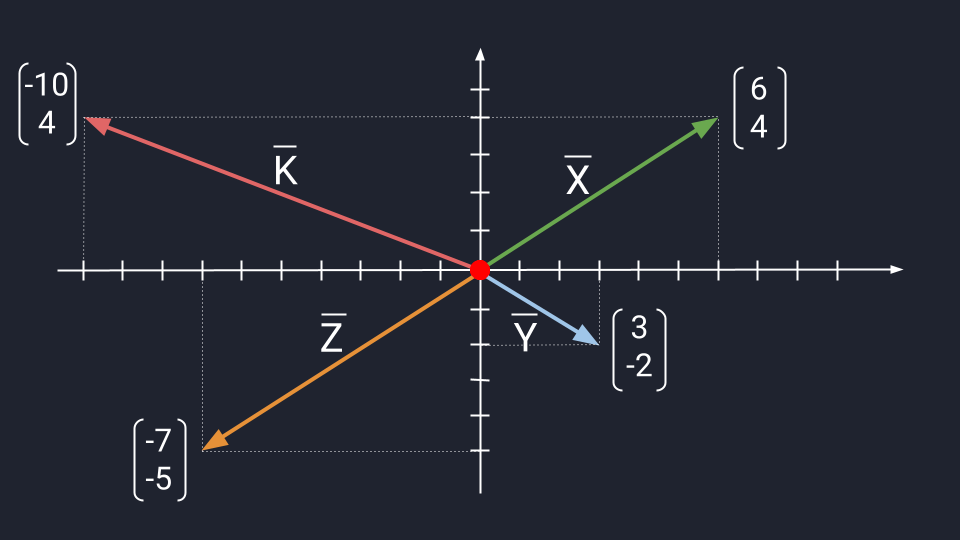
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
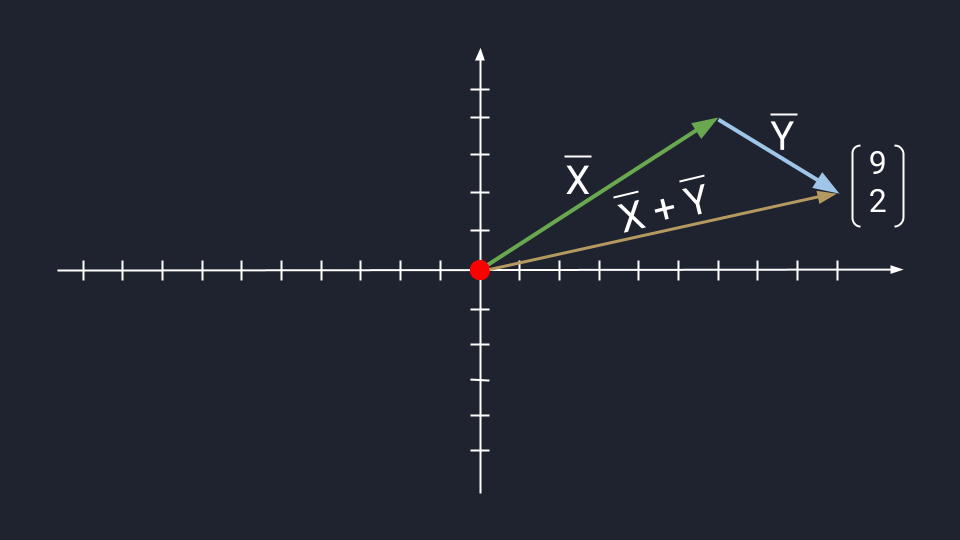
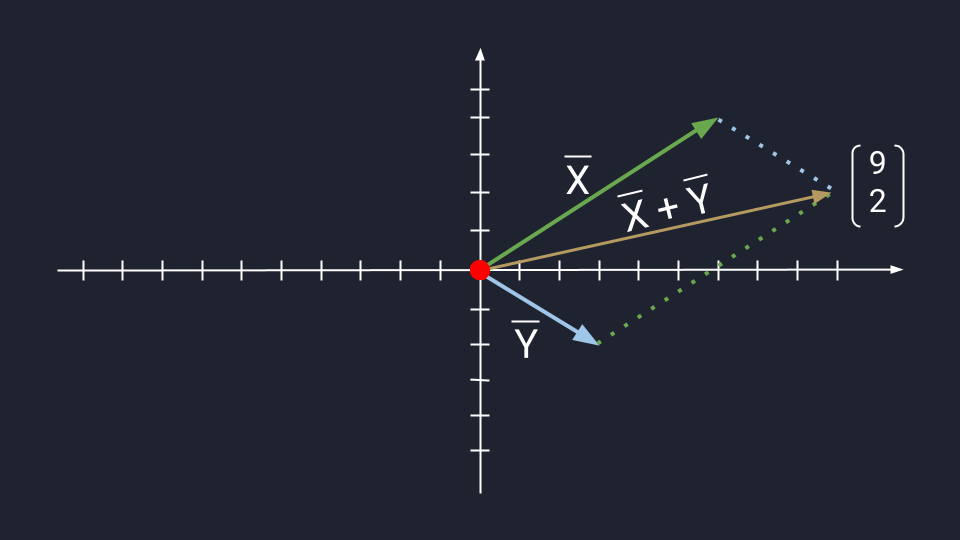
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Видео:10 класс, 42 урок, Умножение вектора на числоСкачать

Вычитание
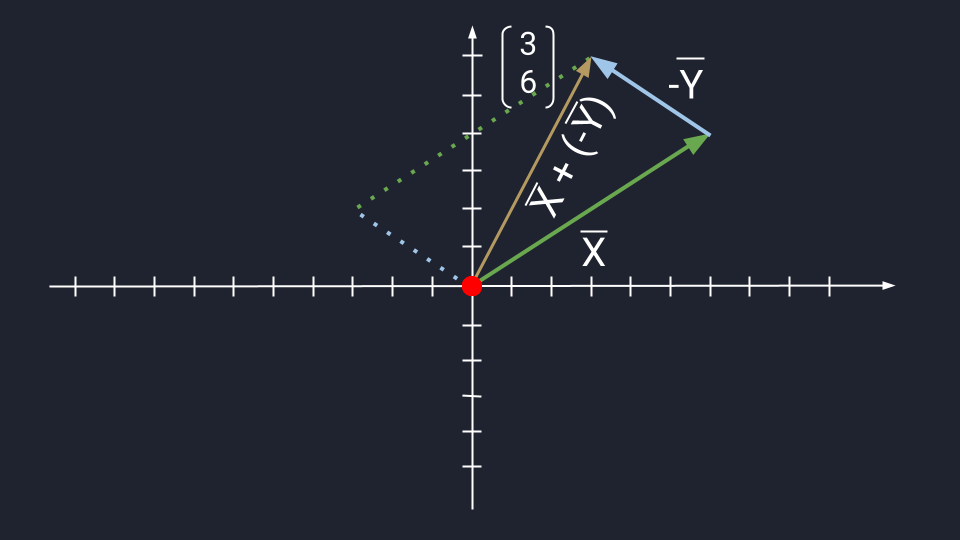
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
- У нас есть X = (6, 4) и Y = (3, −2).
- Превращаем формулу Х − Y в формулу Х + (−Y).
- Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
- Считаем: X + (−Y) = (3, 6).
Теперь посмотрим, как выглядит вычитание векторов на графике:
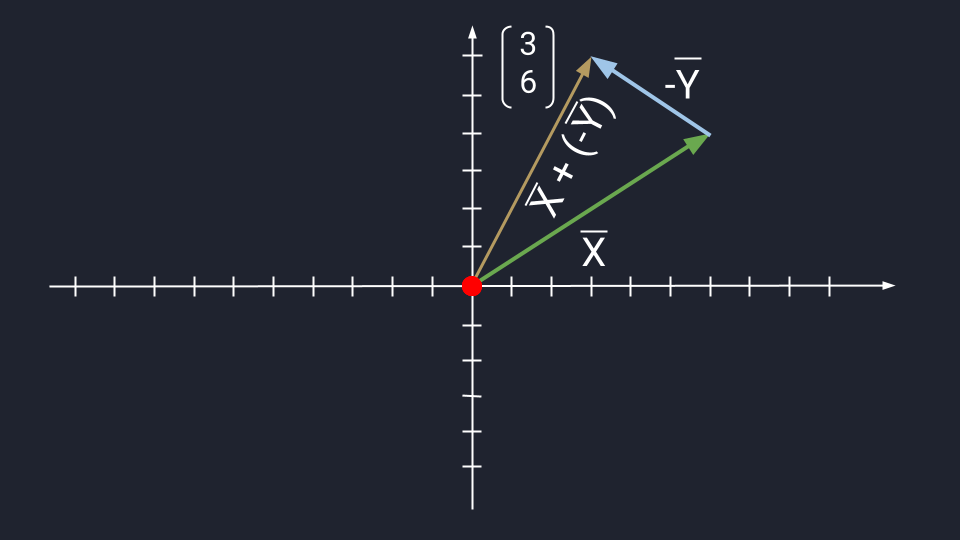
Видео:Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 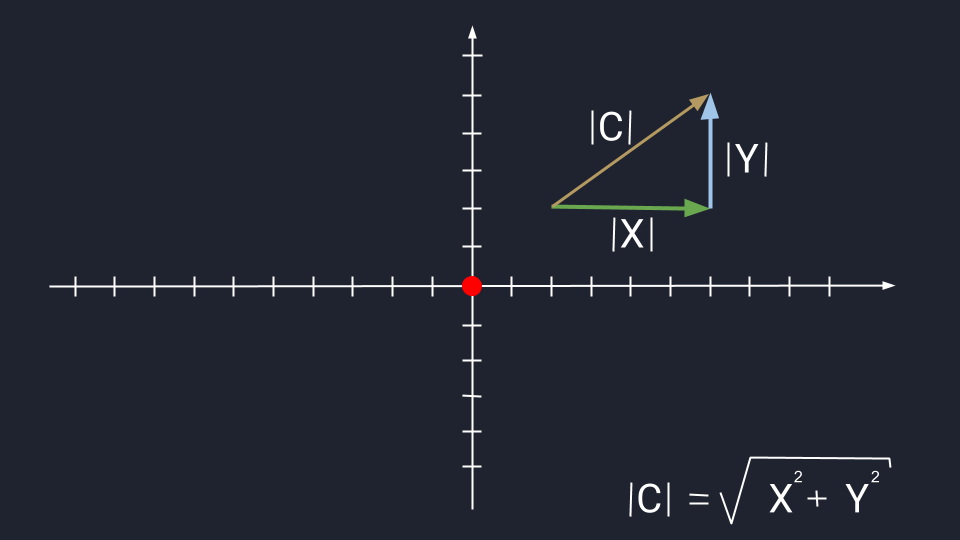
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Видео:8 класс, 47 урок, Произведение вектора на числоСкачать

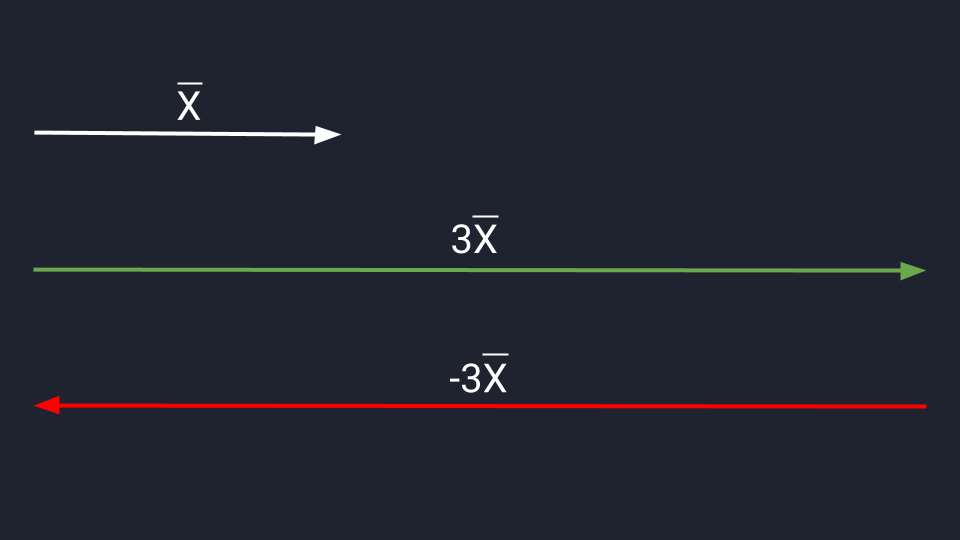
Умножение и деление вектора на число
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
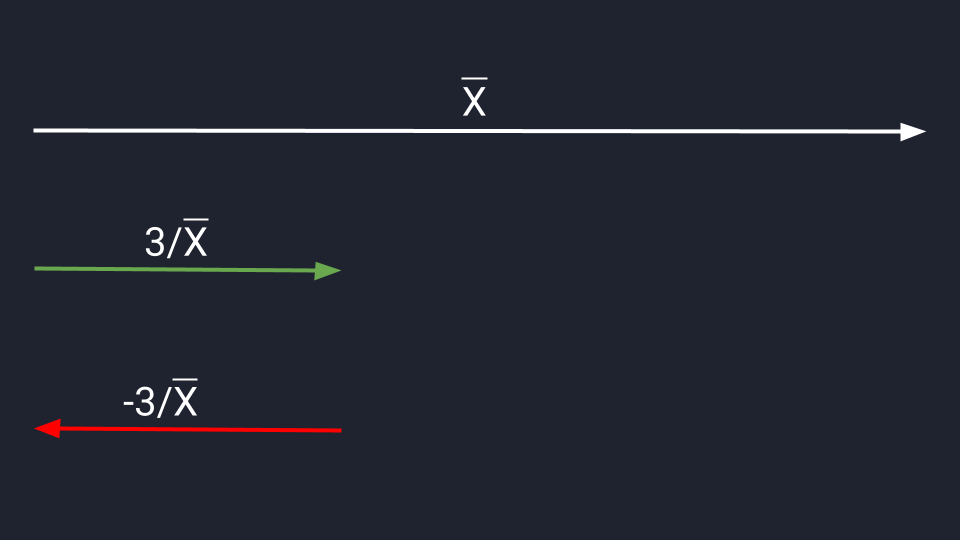
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
Видео:42. Умножение вектора на числоСкачать

Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
- векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
- если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
- а перемножение матриц — это и есть машинное обучение.
Видео:Геометрия 9 класс (Урок№4 -. Умножение вектора на число.)Скачать

Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Видео:Умножение вектора на число. Практическая часть. 9 класс.Скачать

Делить вектор на число онлайн
Этот онлайн калькулятор поможет вам разделить вектор на число. Вы сами будете удивлены, как быстро и легко это делается. А главное, калькулятор никогда не ошибается и выдаёт точный результат.
Видео:умножение ВЕКТОРА на число + теорема о средней линии ТРАПЕЦИИСкачать

Калькулятор
Видео:10 класс, 40 урок, Сложение и вычитание векторовСкачать

Инструкция
Примечание: π записывается как pi; корень квадратный как sqrt().
Шаг 1. Введите в поля данные вектора и число.
Шаг 2. Нажмите кнопку “Поделить”.
Шаг 3. Получите результат.
Вводить можно любые цифры с клавиатуры.
Видео:Вычитание векторов. 9 класс.Скачать

Что такое деление вектора на число
Разделить вектор на число
, значит найти такой вектор, который будучи умножен на число
даст в произведении вектор
.Обозначит можно так:
или
. Вместо деления
можно выполнить и умножение:
Видео:Умножение вектора на число. Практическая часть. 9 класс.Скачать

Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Видео:Умножение вектора на число. Векторы на плоскости. Геометрия 8-9 классСкачать

Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Видео:Геометрия 9 класс. Умножение вектора на числоСкачать

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Видео:УМНОЖЕНИЕ ВЕКТОРА на число 9 класс ЗАДАЧИ геометрия АтанасянСкачать

Умножение вектора на число
При умножении вектора 



Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
🎥 Видео
86. Произведение вектора на числоСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

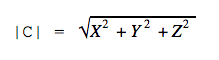
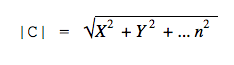

















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»