Уравнение окружности отрицательный радиус

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<y=frac=-frac + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm<R=sqrt=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<y=frac=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

Видео:Уравнение окружности (1)Скачать

Окружность — модель устройства мира

Число Пи ( π ) и Золотая пропорция (φ) связаны абсолютными тождествами (см. Тождественность числа Пи и Золотой пропорции):

При этом 2* π = 360° — это окружность.

Число Пи (выраженное в градусах) — угловая величина и Золотая пропорция – линейная величина, являются различными математическими выражениями одного и того же закона Мироздания, суть которого — целостность и гармоничность мира.

2) Золотая пропорция и уравнение окружности

Золотая пропорция, есть частный случай уравнения окружности x 2 + y 2 = r 2 , при r = 1, а x = y 2 , где x = y 2 – это уравнение параболы (см. Тождественность числа Пи и Золотой пропорции).

Если есть два параметра, числа или явления, связанные между собой Золотой пропорцией, то это говорит о том, что есть также уравнение окружности, включающее в себя эти параметры, т.е. всё, что гармонично, явно или неявно связано функционально через окружность.

3) Теорема Пифагора и окружность

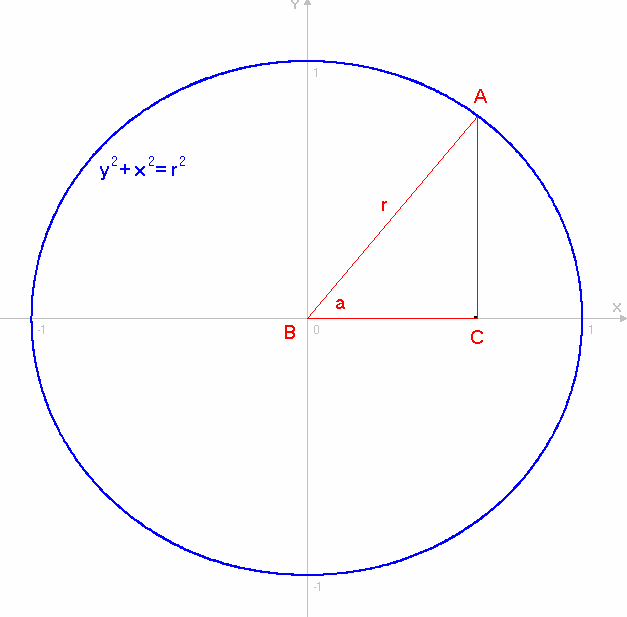
Уравнение окружности задано уравнением x 2 + y 2 = r 2 :

Рассмотрим треугольник ABC:

Т.к. величина ВС равна значению x для точки A, и величина AC равна значению y для точки A, при этом радиус окружности г равен AB, то уравнение окружности x 2 + y 2 = r 2 можно записать в виде:

(ВС) 2 + (AC) 2 = (AB) 2

А это ничто иное, как уравнение прямоугольного треугольника ABC, с катетами AC, ВС, и гипотенузой AB (Теорема Пифагора).

График взаимосвязи параметров x и y, представляет собой, множество всех точек A прямоугольного треугольника ABC, при изменяемых величинах катетов AC, ВС и постоянной величине гипотенузы AB ( r = const ).

4) Окружность и энергия

Число π в угловых единицах измерения — это 180°, и это — ровно половина окружности. Если угол, соответствующий полной окружности — 2 π , обозначить любой другой буквой, например П (П= 2 π = 360°), то уравнение площади круга запишется в виде:

а уравнение периметра окружности запишется в виде:

Сравните полученные формулы с формулой кинетической энергии тела:

и формулой импульса тела:

Не означает ли это принципиальную связь массы тела с числом Пи? Сопоставляя формулы (например, импульса и длины окружности), из размерностей величин входящих в них, можно увидеть, что отношение массы ко времени будет иметь тот же математический смысл, что и число Пи.

p = mV = ml/t, где l — длина, имеющая ту же размерность, что и радиус окружности [м], а t — время [c].

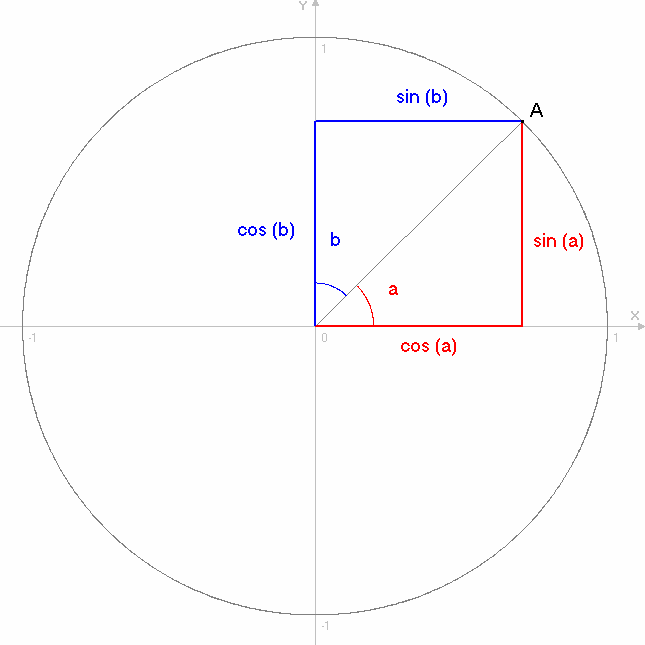
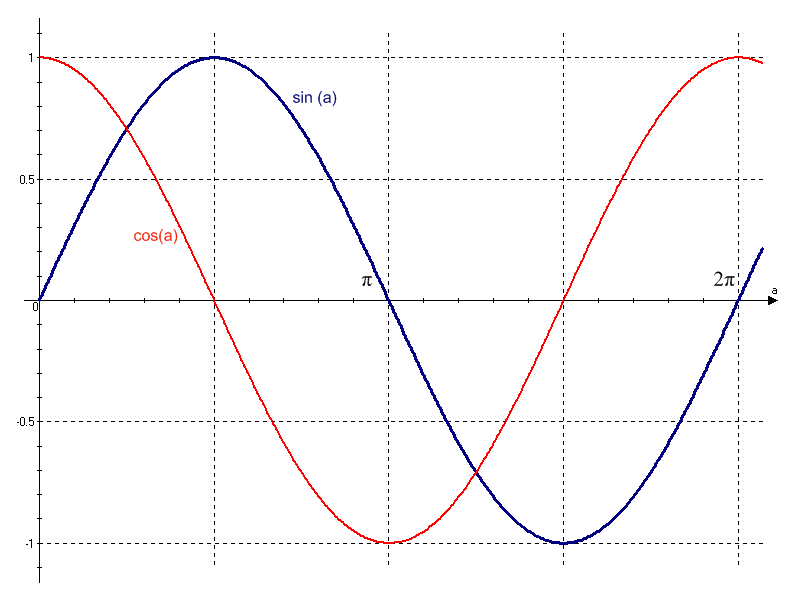
5) Синус, косинус и уравнение окружности

Так как у = sin(a), а x = cos(a), то уравнение окружности с единичным радиусом x 2 + y 2 = 1, можно записать, как:

В этом случае уравнение окружности будет отражать зависимость не от двух параметров х от y, а только от одного — угла a:

Можно перечислить всё, что, так или иначе, связано с окружностью:

• Окружность — это геометрическая фигура.

• Окружность — это траектория движения, орбита.

• Окружность — это цикличность всех процессов происходящих в мире.

• Прямая линия, это крайний случай дуги окружности с бесконечным радиусом. Так как этот случай один из бесконечного числа вариантов, и окружность с бесконечным радиусов в пределах нашей, конечной по размерам, Вселенной существовать не может, то можно утверждать, что в мире нет прямых линий, также, как и нет прямолинейного движения.

• Уравнение окружности можно представить в виде уравнений синуса и косинуса, поэтому все процессы с параметрами, изменяющиемися, как функция синуса или косинуса (а это — электромагнитные излучения, свет, звук, тепловое излучение, радиоволны, рентгеновское излучение и т.д. и т.п.), т.е. все или почти все процессы во Вселенной, являются частью процессов, изменяющихся по уравнению окружности.

• Уравнение, связывающее катеты и гипотенузу прямоугольного треугольника (Теорема Пифагора), есть ни что иное, как уравнение окружности в том виде, что гипотенуза — это радиус окружности, а катеты — это проекции радиуса окружности (гипотенузы) на координатные оси.

• Уравнение окружности включает в себе Золотую пропорцию (как частный случай уравнения окружности), и это позволяет связать музыкальную и эстетическую гармонию, а также целостность Вселенной, с окружностью.

• Косвенно, на связь с уравнением окружности указывает подобие формул кинетической энергии, импульса тела и формул площади круга и длины окружности.

• Окружность в виде сферы – самая распространенная форма во Вселенной. Из всех возможных тел, при условии равенства их объёмов, только сфера имеет самую маленькую площадь поверхности.

И это конечно же, далеко не весь список.

Если человечество когда-либо найдёт универсальное математическое описание всему, что происходит в мире, то нет никаких сомнений, что этим описанием будет формула окружности.

📽️ Видео

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

№966. Напишите уравнение окружности радиуса r с центром А, если: а) А(0;5), r= 3; б) А(-1;2), r = 2Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Найти центр и радиус окружностиСкачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ | 9 класс Алимов | задачи 447 455Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Уравнение окружности. Видеоурок 7. Геометрия 9 классСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Радиус описанной окружностиСкачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать