Точка M — середина стороны AD параллелограмма ABCD . Из вершины A проведены два луча, которые разбивают отрезок BM на три равные части.
а) Докажите, что один из лучей содержит диагональ параллелограмма.
б) Найдите площадь четырёхугольника, ограниченного двумя проведёнными лучами и прямыми BD и BC , если площадь параллелограмма ABCD равна 40.
а) Обозначим точки пересечения лучей с отрезком BM — буквами P и R (см. рисунок), и пусть O — точка пересечения диагоналей параллелограмма, а N — точка пересечения луча AP и прямой BC.
Точка R делит медиану BM треугольника ABD в отношении 2 :1 считая от B. Следовательно, R лежит на медиане AO этого треугольника, то есть луч AR содержит диагональ AC .
б) Пусть L — точка пересечения AN и BD. Нужно найти площадь четырёхугольника LNCO. Пусть площадь параллелограмма равна S . Площадь треугольника BOC равна Найдём площадь треугольника BNL . Из подобия треугольников BPN и MPA следует, что
Теперь из подобия треугольников BNL и DAL следует, что их соответствующие высоты относятся как 1:4 , а поэтому высота треугольника BNL, проведённая к BN, составляет высоты параллелограмма, проведённой к стороне BC.
Следовательно, площадь четырёхугольника LNCO равна
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:Задача с канала PreMath — попробуй найти площадь четырехугольникаСкачать  Найти площадь четырехугольника .найти площадь четырехугольника ограниченного прямыми 2х + 3у=12; 2х+3у=6 и осями координат Первая прямая отсекает на коорд. осях отрезки dx1=6 dy1=4; S1=dx1*dy1/2;=12 вторая прямая: dx2=3; dy2=2; S2=dx2*dy2/2=3. Площадь четырехугольника S=S1-S2=12-3=9 Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать  Формулы вычисления площади произвольного четырёхугольникаВ школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры. Видео:Площадь четырехугольникаСкачать  Определения и соглашенияВ приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Видео:Найдите площадь четырёхугольникаСкачать  Нахождение площади четырёхугольника различными способами и методамиУзнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2). Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных. Теперь пусть даны стороны и противолежащие углы четырёхугольника. Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d). На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров. Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996. Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного. Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным. Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид: Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим: S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных. Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой: S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров. Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим: S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных. Видео:Найти площадь четырехугольника!Скачать  ЗаключениеВнимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра. Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений. Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать  ВидеоРазобраться в этой теме вам поможет видео. 📸 ВидеоПлощади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать  Криволинейная трапеция и ее площадь. 11 класс.Скачать  Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать  Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать  Олимпиадная математика ➜ Найдите площадь четырёхугольника на рисункеСкачать  Вирусная задача ★ Найдите угол на рисунке ★ Три способа решенияСкачать  Вирусная задача. Найти площадь четырёхугольника.Скачать  ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать  Почти никто не решил ★ Красивая геометрия ★ Найдите площадь четырехугольника на рисункеСкачать  Найти площадь 4-ка УСТНО!Скачать  Найдите площадь четырехугольника на рисункеСкачать 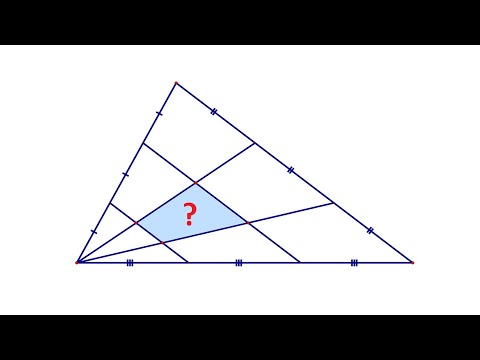 Длина окружности. Площадь круга. 6 класс.Скачать  Геометрия Как найти площадь четырехугольника, если нет формулыСкачать  №481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 смСкачать  |

 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.