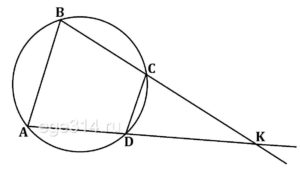
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
Поскольку четырёхугольник ABCD вписанный, сумма углов ABC и ADC равна 180°.
Получаем, что в треугольниках KAB и KCD углы ABK и CDK равны, угол K общий, следовательно, эти треугольники подобны.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Доказательство верное, все шаги обоснованы. | 2 |
| Доказательство в целом верное, но содержит неточности. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |
Аналоги к заданию № 333322: 333348 401596 Все
Видео:Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжениеСкачать

Решение №1222 Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС …
Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСD подобны.
Источник: ОГЭ Ященко 2021 (36 вар)
В ΔКАВ и ΔКСD ∠К общий.
Четырёхугольник АВСD вписан в окружность сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180º
∠ABC = 180º – ∠ADC
∠ADC и ∠СDK смежные их сумма равна 180º:
∠ADC + ∠СDK = 180º
∠СDK = 180º – ∠ADC
Из этих двух равенств получаем:
∠ABC = ∠СDK
Тогда ΔКАВ и ΔКСD подобны по двум равным углам.
Что и требовалось доказать.
Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

ОГЭ. Решение задач по геометрии повышенного уровня сложности
Презентация содержит разбор решения 21 задачи повышенного и высокого уровня сложностей по модулю «Геометрия» и предназначена для подготовки учащихся 9 класса к ГИА.
Просмотр содержимого документа
«ОГЭ. Решение задач по геометрии повышенного уровня сложности»
Подготовка к ГИ А
Модуль «Геометрия» Решение задач повышенного и высокого уровня сложностей
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
Задача 1 (повышенный уровень сложности)
Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе
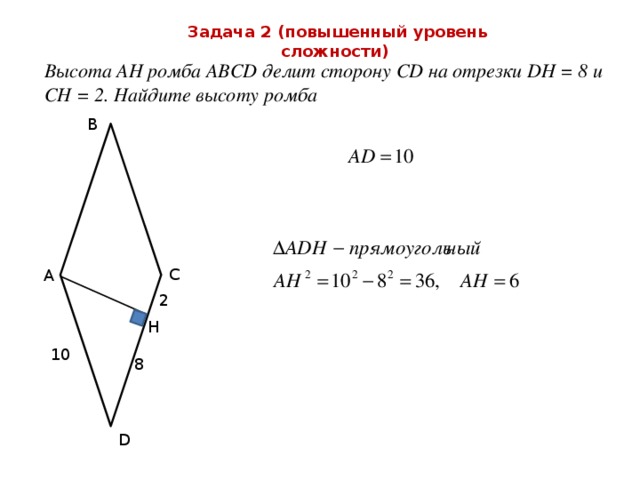
Задача 2 (повышенный уровень сложности)
Высота АН ромба АВСD делит сторону СD на отрезки DН = 8 и СН = 2. Найдите высоту ромба
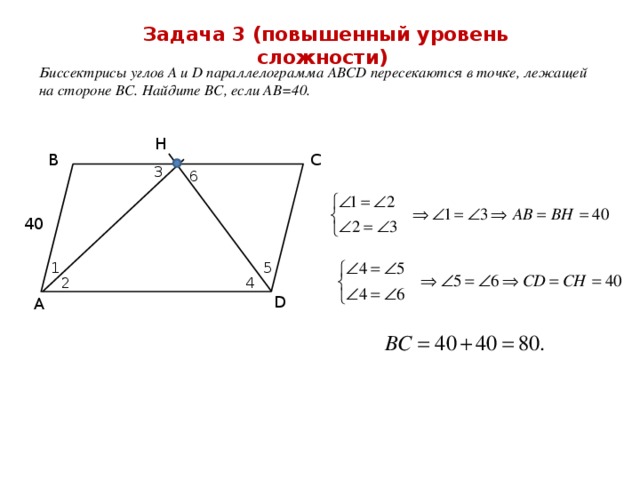
Задача 3 (повышенный уровень сложности)
Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке, лежащей на стороне ВС. Найдите ВС, если АВ=40.
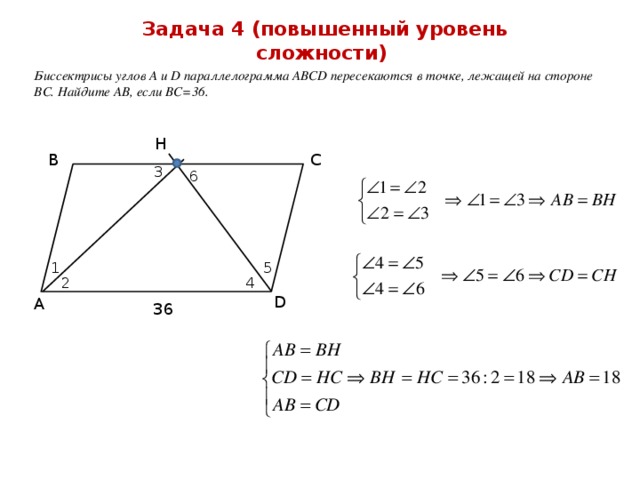
Задача 4 (повышенный уровень сложности)
Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке, лежащей на стороне ВС. Найдите AB, если BC=36.
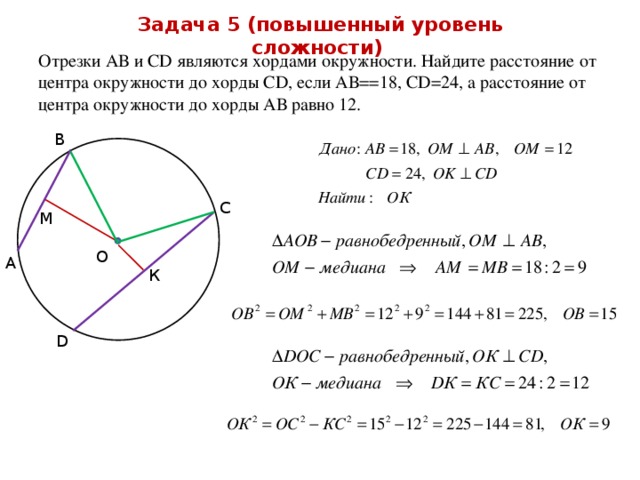
Задача 5 (повышенный уровень сложности)
Отрезки АВ и СD являются хордами окружности. Найдите расстояние от центра окружности до хорды СD, если АВ==18, СD=24, а расстояние от центра окружности до хорды АВ равно 12.
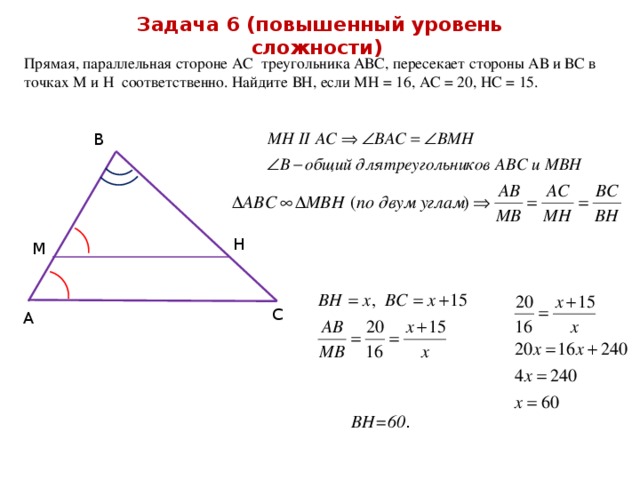
Задача 6 (повышенный уровень сложности)
Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно. Найдите ВН, если МН = 16, АС = 20, НС = 15.
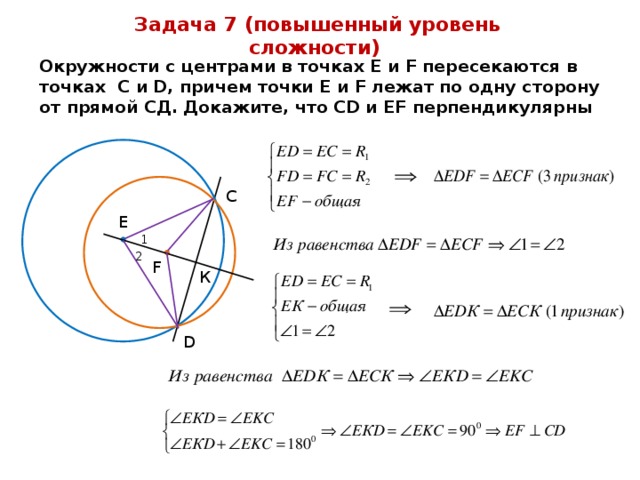
Задача 7 (повышенный уровень сложности)
Окружности с центрами в точках E и F пересекаются в точках C и D, причем точки E и F лежат по одну сторону от прямой СД. Докажите, что CD и EF перпендикулярны
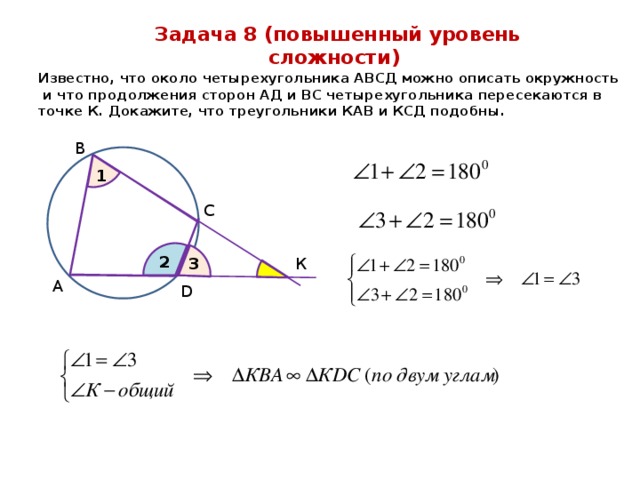
Задача 8 (повышенный уровень сложности)
Известно, что около четырехугольника АВСД можно описать окружность и что продолжения сторон АД и ВС четырехугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСД подобны.
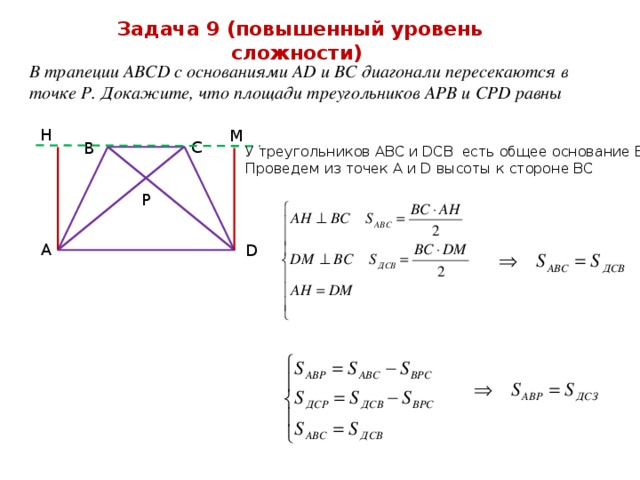
Задача 9 (повышенный уровень сложности)
В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке Р. Докажите, что площади треугольников АРВ и СРD равны
У треугольников АВС и DСВ есть общее основание ВС
Проведем из точек А и D высоты к стороне ВС
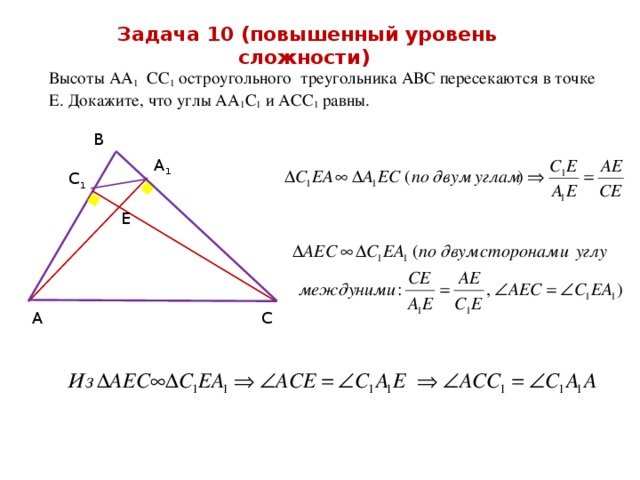
Задача 10 (повышенный уровень сложности)
Высоты АА 1 СС 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы АА 1 С 1 и АСС 1 равны.
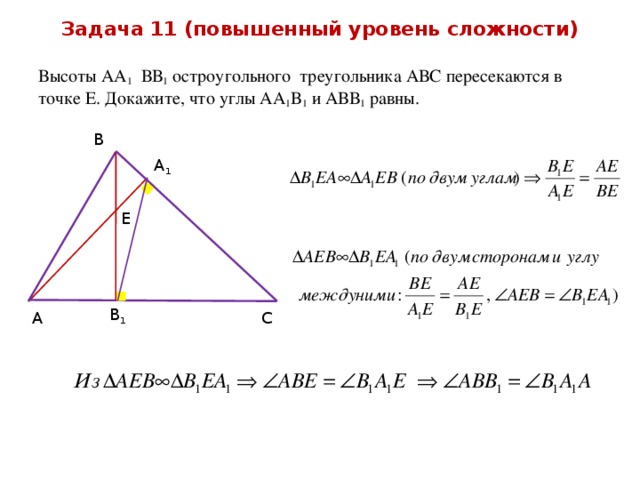
Задача 11 (повышенный уровень сложности)
Высоты АА 1 ВВ 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы АА 1 В 1 и АВВ 1 равны.
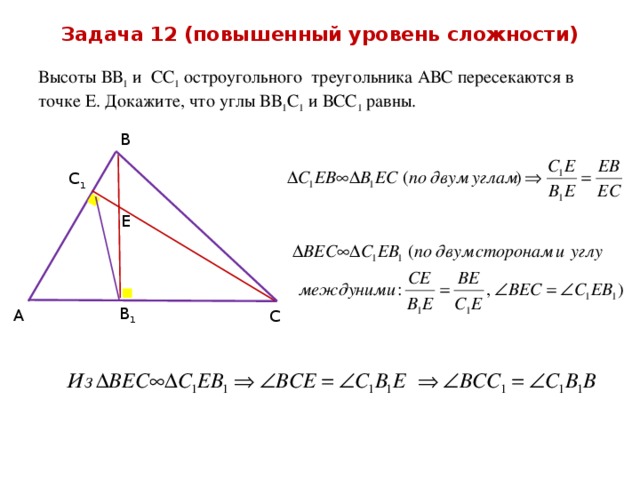
Задача 12 (повышенный уровень сложности)
Высоты ВВ 1 и СС 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы ВВ 1 С 1 и ВСС 1 равны.
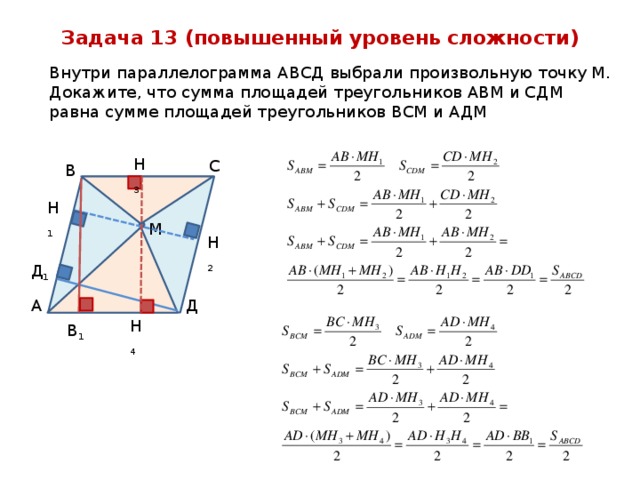
Задача 13 (повышенный уровень сложности)
Внутри параллелограмма АВСД выбрали произвольную точку М. Докажите, что сумма площадей треугольников АВМ и СДМ равна сумме площадей треугольников ВСМ и АДМ
Задача 14 (высокий уровень сложности)
Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР равен 60. Тангенс угла ВАС равен 4/3. Найдите радиус окружности, вписанной в треугольник АВС.
Задача 15 (высокий уровень сложности)
Биссектрисы углов А и В параллелограмма АВСД пересекаются в точке К. Найдите площадь параллелограмма, если ВС = 2, а расстояние от точки К до стороны АВ равно 1.
Точки М, К и Р лежат на одной прямой, МР = КМ + КP = 2
Задача 16 (высокий уровень сложности)
В треугольнике АВС известны длины сторон АВ = 8, АС = 64. Точка О — центр окружности, описанной около треугольника АВС. Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д. Найдите СД.
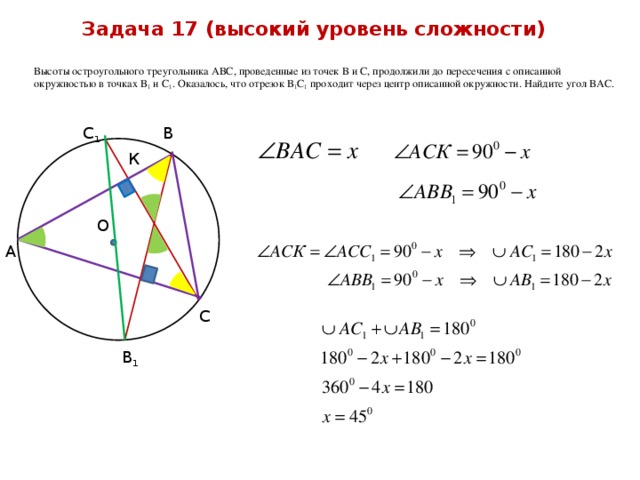
Задача 17 (высокий уровень сложности)
Высоты остроугольного треугольника АВС, проведенные из точек В и С, продолжили до пересечения с описанной окружностью в точках В 1 и С 1 . Оказалось, что отрезок В 1 С 1 проходит через центр описанной окружности. Найдите угол ВАС.
Задача 18 (высокий уровень сложности)
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 33.
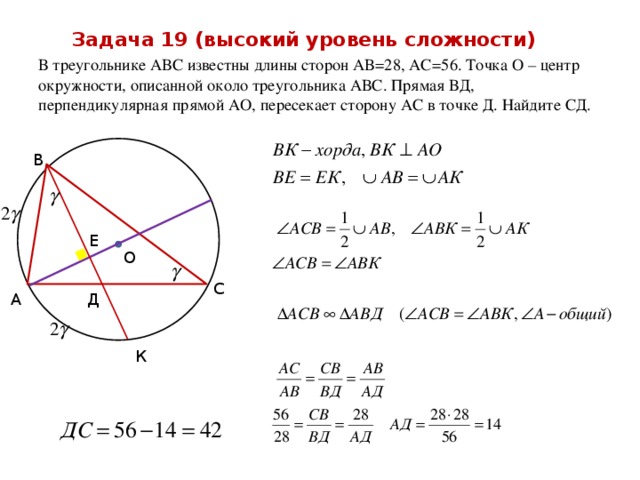
Задача 19 (высокий уровень сложности)
В треугольнике АВС известны длины сторон АВ=28, АС=56. Точка О – центр окружности, описанной около треугольника АВС. Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д. Найдите СД.
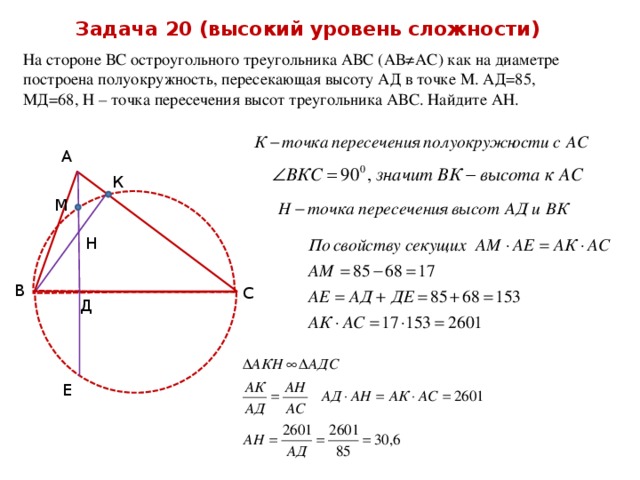
Задача 20 (высокий уровень сложности)
На стороне ВС остроугольного треугольника АВС (АВ≠АС) как на диаметре построена полуокружность, пересекающая высоту АД в точке М. АД=85, МД=68, Н – точка пересечения высот треугольника АВС. Найдите АН.
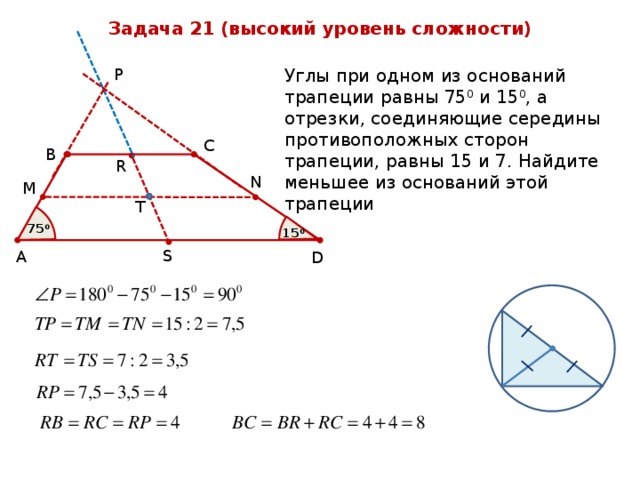
Задача 21 (высокий уровень сложности)
Углы при одном из оснований трапеции равны 75 0 и 15 0 , а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 7. Найдите меньшее из оснований этой трапеции
💥 Видео
Задача 25 ОГЭ Математика 2 ЯщенкоСкачать

Как узнать, что около четырехугольника можно описать окружность?😍 #математика #математикаегэ #егэСкачать
16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

Геометрия Найдите диагональ AC четырехугольника ABCD если около него можно описать окружность и ABСкачать

Геометрия Можно ли описать окружность около четырехугольника ABCD если AB = 4 см AD = 3 см BD = 6смСкачать

Геометрия. Задача. Четырёхугольник. Окружность.Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ОГЭ 2020 по математике. Задание 25 и 26. Вариант 2Скачать

ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Угол А четырёхугольника ABCD, вписанного в окружность, равен 25.Найдите уголСкачать

Все типы 24 задание 2 часть ОГЭ ПО МАТЕМАТИКЕ 2023 УмскулСкачать

ОГЭ 24 КАК РЕШИТЬ ЗАДАЧУ НА ДОКАЗАТЕЛЬСТВО ЧЕТЫРЕХУГОЛЬНИК И ОКРУЖНОСТЬСкачать

Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
8 класс. Четырехугольник и окружностьСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Если в четырёхугольник можно вписать окружностьСкачать

Четырехугольник вписанный в окружность и подобие треугольников. 25 задание ОГЭСкачать

Задание 25 Признак вписанного четырёхугольникаСкачать