Изобразить с помощью кругов эйлера отношения между понятиями четырехугольник

Математика | 10 — 11 классы

Изобразите при помощи кругов отношения между объемами понятий, если : A»четырехугольник», B»трапеция», C»прямоугольник».

Согласно одному из определений трапеции, прямоугольник — тоже является трапецией — имеет одну пару параллельных сторон.

Тогда в большом круге «4 — хугольники» можно вписать средний «трапеции», внутри которого мменьший — «прямоугольники».

Однако есть и другое определение — уточняющее обязательную непараллельность второй парц сторон у трапеции.

Тут надо смотреть определение в твоём учебнике.

В этом случае внутри большого круга «4 — хугольники» надо поместить 2 непересекающихся круга «трапеции» и «прямоугольники».

Видео:Отношения между понятиями ЛОГИКА Урок 5Скачать

Изобразить отношения между объемами следующих понятий на кругах Эйлера — Венна : 1) а : треугольник 2) б : прямоугольный треугольник 3) с : равнобедренный треугольник?

Изобразить отношения между объемами следующих понятий на кругах Эйлера — Венна : 1) а : треугольник 2) б : прямоугольный треугольник 3) с : равнобедренный треугольник.

Видео:Практикум. Логические отношения между понятиями.Скачать

Изобразите при помощи кругов Эйлера отношения между множествами A и B, если A — множество трехзначных чисел , B = ?

Изобразите при помощи кругов Эйлера отношения между множествами A и B, если A — множество трехзначных чисел , B = .

Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Определите отношения между понятиями и изобразите эти отношения в виде кругов эйлера по образцу?

Определите отношения между понятиями и изобразите эти отношения в виде кругов эйлера по образцу.

Понятия конструктор , игрушка , заводная игрушка, заводной автомобиль.

Видео:Простое объяснения решения задач при помощи кругов ЭйлераСкачать

Изобразите с помощью кругов Эйлера отношения между множествами АиB, если А — множество трехзначных чисел B = ?

Изобразите с помощью кругов Эйлера отношения между множествами АиB, если А — множество трехзначных чисел B = .

Видео:Отношения между понятиямиСкачать

Изобразите при помощи кругов Эйлера отношения между множествами С и D, если а) С — множество двузначных чисел и D — множество трехзначных чисел б) С — множество двузначных чисел и D — множество натура?

Изобразите при помощи кругов Эйлера отношения между множествами С и D, если а) С — множество двузначных чисел и D — множество трехзначных чисел б) С — множество двузначных чисел и D — множество натуральных чисел, не меньших 10.

Видео:Круги Эйлера в реальной жизни. Математика на QWERTYСкачать

Изобразите при помощи кругов элера отношения между множествами А и В если А — множество трехзначных чисел кратных 3, В — множество трехзначных чисел делящихся на 6?

Изобразите при помощи кругов элера отношения между множествами А и В если А — множество трехзначных чисел кратных 3, В — множество трехзначных чисел делящихся на 6.

Видео:Отношения между понятиями. Видеоурок по информатике 6 классСкачать

Помогите срочно нужно изобразите при помощи кругов эйлера отношение между тремя пересекающимися множествами А, В и С И отметьте штриховкой области следующих множеств : (СUА) В?

Помогите срочно нужно изобразите при помощи кругов эйлера отношение между тремя пересекающимися множествами А, В и С И отметьте штриховкой области следующих множеств : (СUА) В.

Видео:Решение задач с помощью кругов ЭйлераСкачать

Изобразите при помощи кругов Эйлера отношения между объемами понятий А, В, С, если : А — треугольник, В — равнобедренный треугольник, С — равностороний треугольник?

Изобразите при помощи кругов Эйлера отношения между объемами понятий А, В, С, если : А — треугольник, В — равнобедренный треугольник, С — равностороний треугольник.

Видео:ЛОГИКА: ВИДЫ ПОНЯТИЙ VID 20210419 065122Скачать

Изобразите при помощи кругов Эйлера отношение между множествами A и B, если A = ; B = ?

Изобразите при помощи кругов Эйлера отношение между множествами A и B, если A = ; B = .

Видео:Отношения между понятиямиСкачать

Изобразите с помощью программы Эйлера — Венна отношения между множествами А, В, С, если А : треугольник, В : прямоугольный треугольник, С : равнобедренный треугольник?

Изобразите с помощью программы Эйлера — Венна отношения между множествами А, В, С, если А : треугольник, В : прямоугольный треугольник, С : равнобедренный треугольник.

На этой странице вы найдете ответ на вопрос Изобразите при помощи кругов отношения между объемами понятий, если : A»четырехугольник», B»трапеция», C»прямоугольник»?. Вопрос соответствует категории Математика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

По т. Пифагора квадрат гипотенузы = сумме квадратов катетов. (а + b)² = (a + x)² + ( b + x)² a² + 2ab + b² = a² + 2ax + x² + b² + 2bx + x² Смотри чертёж в приложении 2ax + x² 2bx + x² = 2ab 2x² + 2(a + b) * x = 2ab x² + (a + b) * x = ab x² — (a + b..

Ответ : 160 батоновПошаговое объяснение : Неделя — это 7 дней7 дней — n батонов(n = 280)4 дня — ? Батонов1)280 : 7 = 40(б) в день2)40 * 4 = 160(б)на 4 дня.

84630 : 7 = 12. 090 7 * 131413 = 919891 27648 : 8 = 3456 102050 * 8 = 816400.

Видео:Как изображать множества на диаграммахСкачать

Решение задач с помощью кругов Эйлера

Классы: 5 , 6 , 7

Ключевые слова: круги Эйлера

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Найдено страниц, тыс.

Крейсер и Линкор

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Круги Эйлера и примеры задач на логику

Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.

Видео:круги эйлера и логические отношенияСкачать

Описание схемы кругов Эйлера

Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.

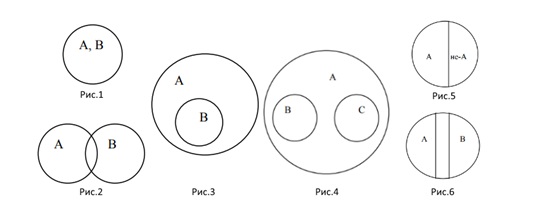
Делятся на группы, в зависимости от типа отношений между множествами:

• равнозначные (рис.1);
• пересекающиеся (рис.2);
• подчиненные (рис.3);
• соподчиненные (рис.4);
• противоречащие (рис.5);
• противоположные (рис.6).

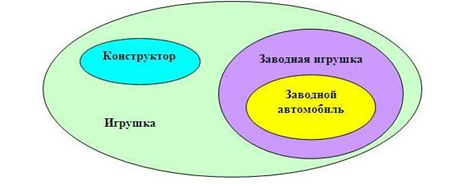
Типовой пример такой диаграммы:

Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.

Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».

Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».

При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.

Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.

Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.

Видео:Круги ЭйлераСкачать

Применение кругов Эйлера

Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.

Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.

Диаграммы делятся на два вида.

Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.

Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров

Видео:Доказать равенства при помощи диаграмм ВеннаСкачать

Примеры задач и решения

Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.

Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.

Задание №1 – начальный уровень.

Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.

Задание №2

Правильный ответ: лягушка.

Задание №3

Правильный ответ: груша.

Задание №4 – средний уровень.

Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.

Задание №5

Правильный ответ: платье.

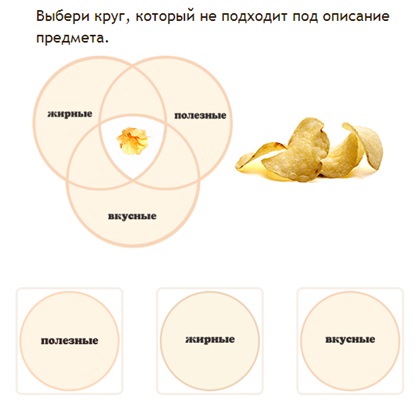
Задание №6

Правильный ответ: полезные.

Задания для школьников

Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.

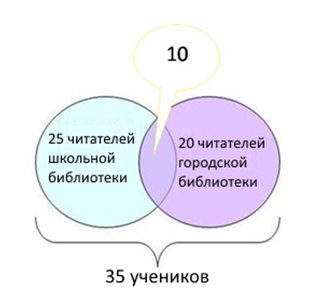
Задание №1

35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.

• Посещают обе библиотеки?
• Не посещают городскую библиотеку?
• Не посещают школьную библиотеку?
• Ходят только в городскую библиотеку?
• Ходят только в школьную библиотеку?

Ответ:

• Определим количество посетителей двух библиотек – общая часть на диаграмме:

• Ученики, не посещающие городскую библиотеку:

35 – 20 = 15 – левая сектор голубой зоны.

• Ученики, не посещающие школьную библиотеку:

35 – 25 = 10 – правый сектор фиолетовой.

• Посетители только городской библиотеки:

35 – 25 = 10 – также, правый сектор фиолетовой.

• Посетители только школьной библиотеки:

35 – 20 = 15 – также, левый сектор голубой.

Задание №2 – также предназначено для младших классов, но является более сложным.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.

1. Есть ли ученики, увлекающиеся всеми спортивными играми?
2. Какое количество школьников интересуется только одной из спортивных игр?

Ответ:

Все ученики класса – наибольшая окружность.

Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.

Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».

16 – (4 + Z + 3) = 9 – Z.

По аналогии, находим количество хоккеистов.

17 – (4 + Z + 5) = 8 – Z.

18 – (3 + Z + 5) = 10 – Z.

Чтобы пределить значение Z, нужно суммировать множества учеников.

3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;

Соответственно, Б = 7, Ф = 8, Х = 6.

Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.

Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.

📹 Видео

Глава 4. Логические категории и отношения между понятиями. Учебник логики. Георгий Челпанов.Скачать

Логика. Лекция 2. Логические операции с понятиямиСкачать

Информатика 4 кл/Н.В.Матвеева/ Тема 9: Отношения между понятиями/19.11.22 12:33Скачать

Операции над множествамиСкачать

Отношения между понятиямиСкачать