Геометрия | 10 — 11 классы
Центр описанной около равнобедренного треугольника окружности делит высоту в отношении 5 : 3, считая от вершины.
Найти площадь треугольника, если основание равно 8.
Пусть дан треугольник АВС, BК = BО + ОКх — 1часть
Треугольник АОС — равнобедрнный, АК = 4см и ОК = 3х⇒АО = √16 + 9х²
АО = ВО — радиусы описанной окружности
S = 1 / 2AC * BK = 1 / 2 * 8 * 8 = 32см².
- Прошу, помогите?
- В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см?
- Помогите решить пожалуйста?
- Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см?
- Центры описанной окружности лежит на высоте равнобедренного треугольника и делит на отрезки равные 5 и 13 см найти площадь этого треугольника?
- В равнобедренном треугольнике центр описанной окружности делит высоту треугольника в отношении 12 : 5?
- Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту, равен 5 см, а основание треугольника равно 24 см?
- Центр окружности, описанной около равнобедренного треугольника, делит медиану, проведенную к основанию, в отношении 25 : 7?
- Помогите пожалуйста?
- Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см?
- Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см. Основание треугольника равно
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Центр описанной окружности делит высоту равнобедренного треугольника в отношении
- 📺 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Прошу, помогите?
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки равные 5 см и 13 см Найти площадь треугольника.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см?
В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см.
Найти основание треугольника.
Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Помогите решить пожалуйста?
Помогите решить пожалуйста!
1о. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD.
Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD.
2о. Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту , равен 8см, а основание треугольника равно 12см.
Найти площадь этого треугольника.
3о. Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см.
Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Видео:Формулы равностороннего треугольника #shortsСкачать

Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см?
Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см.
Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

Центры описанной окружности лежит на высоте равнобедренного треугольника и делит на отрезки равные 5 и 13 см найти площадь этого треугольника?
Центры описанной окружности лежит на высоте равнобедренного треугольника и делит на отрезки равные 5 и 13 см найти площадь этого треугольника.
Видео:Задание 24 ОГЭ по математике вариант №87Скачать

В равнобедренном треугольнике центр описанной окружности делит высоту треугольника в отношении 12 : 5?
В равнобедренном треугольнике центр описанной окружности делит высоту треугольника в отношении 12 : 5.
Найдите площадь этого треугольника, если длина боковой стороны равна 60.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту, равен 5 см, а основание треугольника равно 24 см?
Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту, равен 5 см, а основание треугольника равно 24 см.
Найдите радиус окружности.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

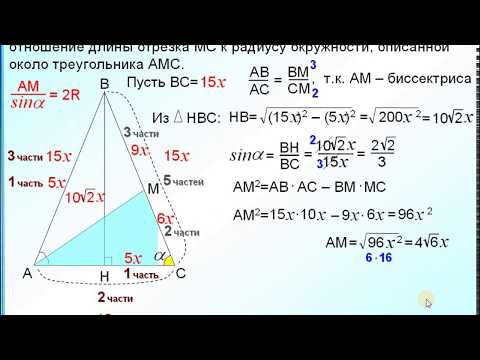
Центр окружности, описанной около равнобедренного треугольника, делит медиану, проведенную к основанию, в отношении 25 : 7?
Центр окружности, описанной около равнобедренного треугольника, делит медиану, проведенную к основанию, в отношении 25 : 7.
Боковая сторона треугольника равна 40 см.
Найдите радиус окружности, вписанной в треугольник.
Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Помогите пожалуйста?
Около остроугольного равнобедренного треугольника описана окружность.
Высота, опущенная из вершины на основание делится центром окружности на отрезки 17 и 8 см ( считая от вершины).
Найдите площадь треугольника.
Помогите пожалуйста, срочно нужно!
Видео:Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см?
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см.
Найдите площадь треугольника.
На этой странице находится вопрос Центр описанной около равнобедренного треугольника окружности делит высоту в отношении 5 : 3, считая от вершины?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Т. к. Треугл р / б то углы при основании равны(по 40°) значит тупой угол = 180 — (40 + 40) = 100°.
Проведем высоты из вершин В и С Средняя линия = (АD + BC) / 2 = (AE + EF + FD + BC) / 2 Т. К. трапеция равнобедренная, то FD = AE BC = EF Ср. Линия = (AE + EF + AE + EF) / 2 = AE + EF = AF а AF можно найти из треугольника ACF AF = AC / Корень(2) = ..
Решение на фото . Надеюсь всё поймешь.
8. 360 — 230 = 130 — сумма углов А и Д 130 / 2 = 65 — угол С.
Ответ с решением приведён на данном изображении.
Т. к. AB = BC, треугольник равнобедренный, это значит, что угол BAC = углу BCA. Сумма углов в треугольнике = 180. Поэтому BCA + BAC + ABC = 180, но BAC = BCA 2BCA + 148 = 180 2BCA = 180 — 148 2BCA = 32 BCA = 16.
1) 6 * 12 = 72 (м2) — площадь участка 2) 6 * 7 = 42 (м2) — площадь участка, засаженного газонной травой 3) 72 — 42 = 30 (м2) — площадь участка, отведённого под розы.
1) Т. К ∠AOC центральный, то ∪AC = 80° 2) Т. К ∠ABC вписанный, то ∠ABC = 1 / 2∪AC = 40° 3) Доп. Построение : АС Т. К ΔАВС равнобедренный, то ∠BAC = ∠BCA = (180° — 40°) : 2 = 70° Т. К ∠BAC вписанный, то ∪АВ = 2∠ВАС = 70° * 2 = 140° Ответ : ∠АВС =..
Сумма углов треугольника 180° 5 : 1 : 3 Т. Е. всего частей 5 + 1 + 3 = 9 частей 180° : 9 = 20° одна часть Углы треугольника соотносятся как 5 * 20° : 20° : 20° * 3 100° : 20° : 60°.
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см. Основание треугольника равно
Видео:Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
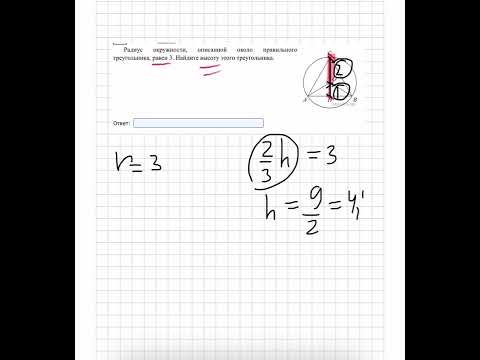
Ваш ответ
Видео:Радиус описанной окружностиСкачать

решение вопроса
Видео:ОГЭ Задание 26 Радиус описанной окружностиСкачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,036
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Радиус окружности описанной около равностороннего треугольникаСкачать
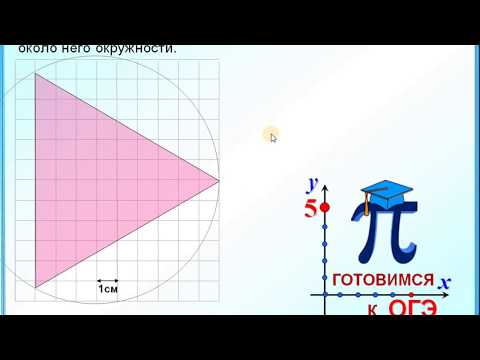
Центр описанной окружности делит высоту равнобедренного треугольника в отношении
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
| Время | |
| Прошло | 0:00:00 |
| Осталось | 3:55:00 |
Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
📺 Видео
7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задание 16 ЕГЭ по математике #6Скачать
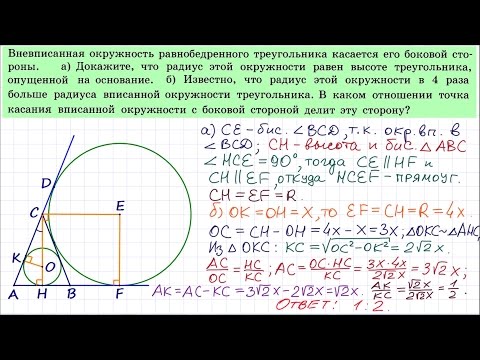
№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать









