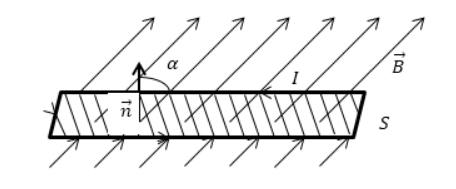
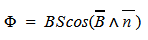Потоком вектора магнитной индукции В (магнитным потоком) через малую поверхность площадью dS называется скалярная физическая величина, равная
Здесь 
, 
— единичный вектор нормали к площадке площадью dS, Вn — проекция вектора В на направление нормали, 
— угол между векторами В и n (рис. 6.28).
Рис. 6.28. Поток вектора магнитной индукции через площадку
Магнитный поток ФB через произвольную замкнутую поверхность S равен
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S выполняется условие
Формула (6.28) выражает теорему Остроградского — Гаусса для вектора 
:
Поток вектора магнитной индукции через произвольную замкнутую поверхность тождественно равен нулю.
Подчеркнем еще раз: эта теорема является математическим выражением того факта, что в природе отсутствуют магнитные заряды, на которых начинались бы и заканчивались линии магнитной индукции, как это имело место в случае напряженности электрического поля Е точечных зарядов.
Это свойство существенным образом отличает магнитное поле от электрического. Линии магнитной индукции замкнуты, поэтому число линий, входящих в некоторый объем пространства, равно числу линий, выходящих из этого объема. Если входящие потоки брать с одним знаком, а выходящие — с другим, то суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю.
В системе СИ единицей измерения магнитного потока является вебер (Вб) (рис. 6.29):
Рис. 6.29. В. Вебер (1804–1891) — немецкий физик
Отличие магнитного поля от электростатического проявляется также в значении величины, которую мы называем циркуляцией — интеграла от векторного поля по замкнутому пути. В электростатике равен нулю интеграл
взятый по произвольному замкнутому контуру. Это связано с потенциальностью электростатического поля, то есть с тем фактом, что работа по перемещению заряда в электростатическом поле не зависит от пути, но лишь от положения начальной и конечной точек.
Посмотрим, как обстоит дело с аналогичной величиной для магнитного поля. Возьмем замкнутый контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В, то есть
Как было получено выше, магнитная индукция, создаваемая прямолинейным проводником с током на расстоянии R от проводника, равна
Рассмотрим случай, когда контур, охватывающий прямой ток, лежит в плоскости, перпендикулярной току, и представляет собой окружность радиусом R с центром на проводнике. В этом случае циркуляция вектора В по этой окружности равна
Можно показать, что результат для циркуляции вектора магнитной индукции не меняется при непрерывной деформации контура, если при этой деформации контур не пересекает линий тока. Тогда в силу принципа суперпозиции циркуляция вектора магнитной индукции по пути, охватывающем несколько токов, пропорциональна их алгебраической сумме (рис. 6.30)
Рис. 6.30. Замкнутый контур (L) с заданным направлением обхода.
Изображены токи I1, I2 и I3, создающие магнитное поле.
Вклад в циркуляцию магнитного поля вдоль контура (L) дают только токи I2 и I3
Если выбранный контур не охватывает токов, то циркуляция 
по нему равна нулю.
При вычислении алгебраической суммы токов следует учитывать знак тока: положительным будем считать ток, направление которого связано с направлением обхода по контуру правилом правого винта. Например, вклад тока I2 в циркуляцию — отрицательный, а вклад тока I3 — положительный (рис. 6.18). Воспользовавшись соотношением
между силой тока I через любую замкнутую поверхность S и плотностью тока 
, для циркуляции вектора В можно записать
где S — любая замкнутая поверхность, опирающаяся на данный контур L.
Циркуляция магнитной индукции отлична от нуля, если контур, по которому она берется, охватывает ток.
Такие поля называются вихревыми. Поэтому для магнитного поля нельзя ввести потенциал, как это было сделано для электрического поля точечных зарядов. Наиболее наглядно разницу потенциального и вихревого полей можно представить по картине силовых линий. Силовые линии электростатического поля похожи на ежей: они начинаются и кончаются на зарядах (либо уходят в бесконечность). Силовые линии магнитного поля никогда не напоминают «ежей»: они всегда замкнуты и охватывают текущие токи.
Для иллюстрации применения теоремы о циркуляции найдем другим методом уже известное нам магнитное поле бесконечного соленоида. Возьмем прямоугольный контур 1-2-3-4 (рис. 6.31) и вычислим циркуляцию вектора В по этому контуру
Рис. 6.31. Применение теоремы о циркуляции В к определению магнитного поля соленоида
Второй и четвертый интегралы равны нулю в силу перпендикулярности векторов 
и 
. Третий интеграл можно положить равным нулю, ввиду малости магнитного поля вне соленоида. Поэтому
Рассмотренный контур охватывает суммарный ток nlI, где n — число витков соленоида, приходящееся на единицу длины, I — сила тока в соленоиде. Следовательно,
Мы воспроизвели результат (6.20) без интегрирования магнитных полей от отдельных витков.
Полученный результат (6.35) можно использовать для нахождения магнитного поля тонкого тороидального соленоида (рис.6.32).
Рис. 6.32. Тороидальная катушка: линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рисунке
Дополнительная информация
Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать
Поток вектора магнитной индукции
Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:
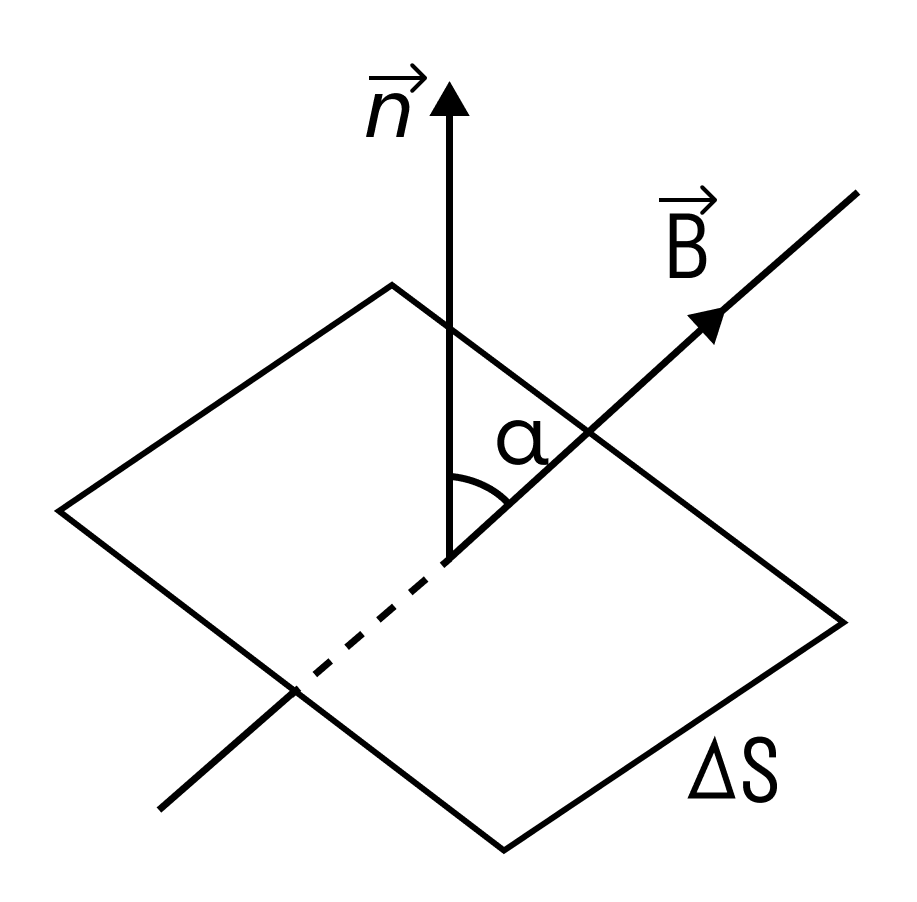
Φ = B S cos α = B n S = B → S → с углом между n → и B → , обозначаемым α , n → является нормалью к площадке S .
Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать
Формула магнитного потока
Φ равняется количеству линий магнитной индукции, пересекающих площадку S , как показано на рисунке 1 . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.
Видео:Поток вектора магнитной индукцииСкачать
В чем измеряется магнитный поток
В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки d S , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока d Φ производится через эту поверхность. Запись примет вид:
d Φ = B d S cos α = B → d S → .
Нахождение полного потока через поверхность S :
Φ = ∫ S B d S cos α = ∫ S B → d S → .
Основной единицей измерения магнитного потока в системе СИ считаются веберы ( В б ) . 1 В б = 1 Т л 1 м 2 .
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δ A , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции d Φ :
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
A = I Φ 2 — Φ 1 с Φ 1 , обозначаемым потоком через контур в начале перемещения, Φ 2 является потоком через контур в конце перемещения.
Видео:Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:
Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
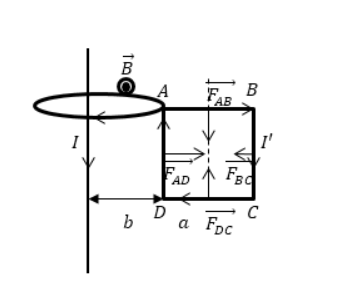
Дан бесконечно длинный прямой проводник с током I , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I ‘ . Сторона рамки равна a . Она располагается в одной плоскости с проводом, как показано на рисунке 2 . Значение расстояния от ближайшей стороны рамки до проводника равняется b . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
A = I ‘ Φ 2 — Φ 1 ( 1 . 1 ) , где I ‘ принимают за силу тока в рамке, Φ 1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b . Φ 2 = 0 . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы ( 1 . 1 ) изменится:
A = — I ‘ Φ 1 ( 1 . 2 ) .
Перейдем к нормали n → и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n → и вектором B → равняется π . Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:
d Φ = — B d S = — B · a · d x = — μ 0 2 π I l d x x ( 1 . 3 ) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:
B = μ 0 2 π x I l ( 1 . 4 ) .
Отсюда следует, что для нахождения всего потока из ( 1 . 3 ) потребуется:
Φ 1 = ∫ S — μ 0 2 π I l d x x = — μ 0 2 π I l ∫ b b + a d x x = — μ 0 2 π I l · ln b + a b ( 1 . 5 ) .
Произведем подстановку формулы ( 1 . 5 ) в ( 1 . 2 ) . Искомая работа равняется:
A = I ‘ μ 0 2 π I l · ln b + a b .
Ответ: A = μ 0 2 π I I ‘ l · ln b + a b .
Найти силу, действующую на рамку, из предыдущего примера.
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние d x . Это говорит о совершении силой работы, равной:
δ A = F d x ( 2 . 1 ) .
Элементарная работа δ A может быть выражена как:
δ A = I ‘ d Φ ( 2 . 2 ) .
Произведем то же с силой, применяя формулы ( 2 . 1 ) , ( 2 . 2 ) . Получаем:
F d x = I ‘ d Φ → F = I ‘ d Φ d x ( 2 . 3 ) .
Используем выражение, которое было получено в примере 1 :
d Φ = — μ 0 2 π I l d x x → d Φ d x = — μ 0 2 π I l x ( 2 . 4 ) .
Произведем подстановку d Φ d x в ( 2 . 3 ) . Имеем:
F = I ‘ μ 0 2 π I l x ( 2 . 5 ) .
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:
F A B → + F D C → = 0 ( 2 . 6 ) , то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
F → = F A D → + F B C → ( 2 . 6 ) .
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
F = F A D — F B C ( 2 . 7 ) .
Произведем поиск силы F A D , действующей на сторону A D , применив формулу ( 2 . 5 ) , где x = b :
F A D = I ‘ м 0 2 π I l b ( 2 . 8 ) .
Значение F B C будет:
F B C = I ‘ μ 0 2 π I l b + a ( 2 . 9 ) .
Для нахождения искомой силы:
F = I ‘ μ 0 2 π I l b — I ‘ μ 0 2 π I l b + a = I I ‘ μ 0 l 2 π 1 b — 1 b + a .
Ответ: F = I I ‘ μ 0 l 2 π 1 b — 1 b + a . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.
Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать
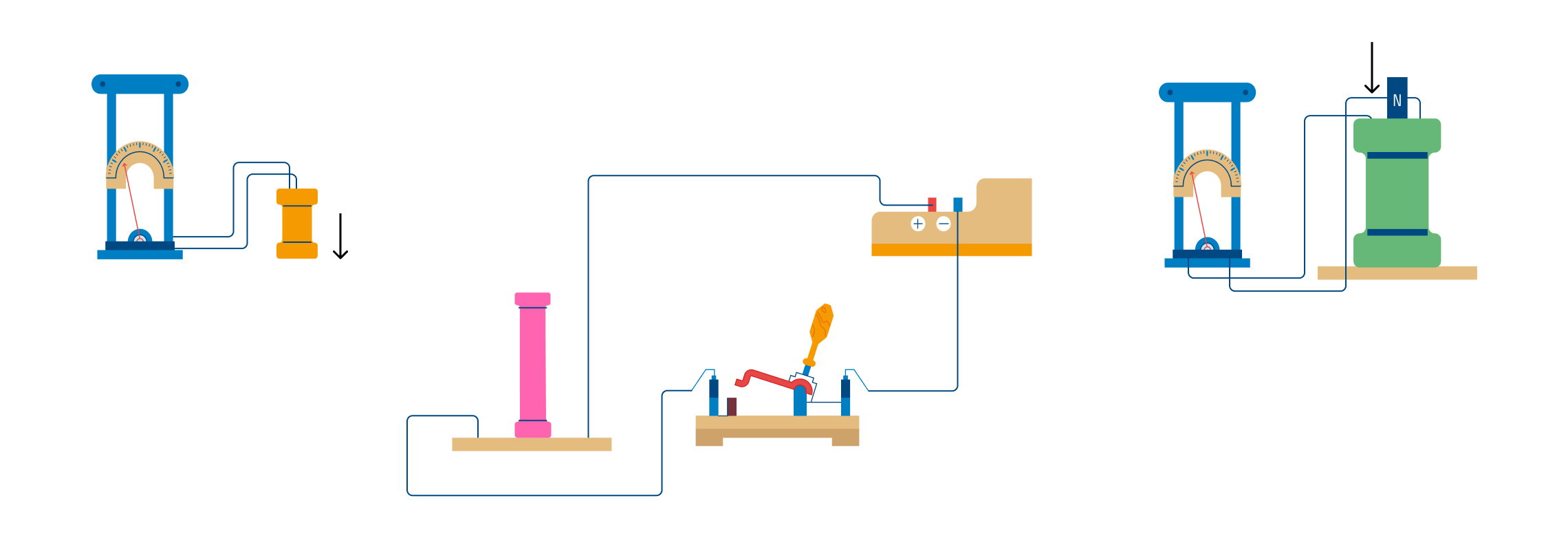
Закон электромагнитной индукции
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать
Магнитный поток
Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.
Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.
Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции B, площади поверхности S, пронизываемой данным потоком, и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
