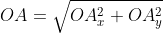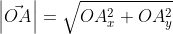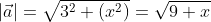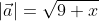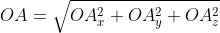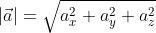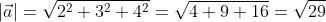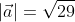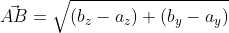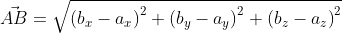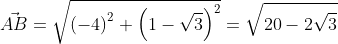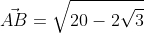Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Выберите документ из архива для просмотра:
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Онлайн калькулятор. Модуль вектора. Длина вектора
- Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам
- Инструкция использования калькулятора для вычисления длины вектора
- Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)
- Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)
- Вычисления длины вектора (модуля вектора)
- Длина вектора — основные формулы
- Основные понятия вектора
- Как найти длину вектора
- Длина вектора через координаты точек начала и конца
- Длина вектора по теореме косинусов
- Применение векторов в других сферах
- 📽️ Видео
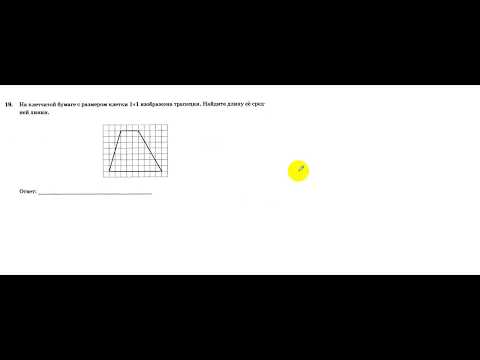
Видео:На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.Скачать
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Решение заданий.docx
Решение заданий №19(задания на клетчатой бумаге)
1.Основные типы задач
Определение тангенса угла;
Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);
Определение расстояния от точки до прямой (отрезка);
Определение длины средней линии треугольника и трапеции;
Определение длины большего катета, большей диагонали;
Определение площади сложных или составных фигур;
Определение градусной меры вписанного угла.
1.Определение тангенса угла
Найдите тангенс угла А треугольника ABC, изображённого на рисунке 1.
Найдите тангенс угла AOB, изображённого
на рисунке 3.
Достроим до прямоугольного треугольника СОВ.
2. Определение площади фигуры
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм (рис. 7). Найдите его площадь.
На клетчатой бумаге с размером клетки 1×1 изображён ромб (рис. 9). Найдите площадь этого ромба.
1. Проведем диагонали.
2. Найдем площадь
3. Определение расстояния от точки до прямой (отрезка)
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C (рис. 11). Найдите расстояние от точки A до середины отрезка BC.
Построим отрезок ВС и
отметим его середину т.О.
2. Соединим т.А с т.О. Получа-
ем нужное расстояние:
4. Определение длины средней линии треугольника и трапеции
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC (рис. 14). Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция (рис. 15). Найдите длину её средней линии.
Основания трапеции соответствен-но равны 7 и 1
5. Определение длины большего катета, большей диагонали
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник (рис. 16). Найдите длину его большего катета.
По рисунку видно, что длина
большего катета = 6.
6. Определение площади сложных или составных фигур
На клетчатой бумаге с размером клетки 1×1 изображена фигура (рис. 18). Найдите её площадь.
Посчитаем количество клеток внутри закрашенной области: их 19
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке 19.
Решение: 1 способ (рис. 19.1)
Найдём площадь данной фигуры по формуле Пика:
Решение: 2 способ (рис.19.2)
Площадь данной фигуры
равна разности площади
квадрата и двух треугольников:
7. Определение градусной меры вписанного угла
Найдите угол ABC (рис. 20). Ответ дайте в градусах.
Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.
Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°.
Задачи для самостоятельно решения
Определение тангенса угла 
Найдите тангенс угла А треугольника, изображённого на рисунке.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке. 
Найдите тангенс углаAOB, изображённого на рисунке. 
Найдите тангенс углаAOB, изображённого на рисунке. 
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс углаAOB. 
Найдите тангенс углаAOB. 
Найдите тангенс угла AOB. 
Найдите тангенс угла, изображённого на рисунке.
Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника)
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь. 
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите его площадь. 
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. 
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь. 
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь. 
Определение расстояния от точки до прямой (отрезка)
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах. 
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.
Определение длины средней линии треугольника и трапеции
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. 
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. 
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC. 
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 
Определение длины большего катета, большей диагонали
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета. 
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета. 
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета. 
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. 
Определение площади сложных или составных фигур
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь. 
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь. 
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке. 
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке. 
Определение площади сложных или составных фигур
Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах. 
Найдите угол ABC . Ответ дайте в градусах. 
Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
I . Определение тангенса угла
II . Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника
III . Определение расстояния от точки до прямой (отрезка)
IV . Определение расстояния от точки до прямой (отрезка)
V . Определение длины большего катета, большей диагонали
VI . Определение площади сложных или составных фигур
VII .Определение площади сложных или составных фигур
Открытый банк заданий ОГЭ http :// oge . fipi . ru
Выбранный для просмотра документ мастер класс.pptx
Описание презентации по отдельным слайдам:
Решение заданий №19 (задания на клетчатой бумаге) Составила учитель математики МБОУ «Виноградовская средняя школа» Безклейная Светлана Александровна
Основные типы задач Определение тангенса угла; Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника); Определение расстояния от точки до прямой (отрезка); Определение длины средней линии треугольника и трапеции; Определение длины большего катета, большей диагонали; Определение площади сложных или составных фигур; Определение градусной меры вписанного угла.
При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь. По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.
Определение тангенса угла
Определение тангенса угла
Определение тангенса угла
Определение тангенса угла
Определение тангенса угла
Определение тангенса угла
Определение тангенса угла
Определение площади фигуры
Определение площади фигуры
Определение площади фигуры
Определение площади фигуры
Определение площади фигуры
Определение расстояния от точки до прямой (отрезка) Что нужно вспомнить: Расстояние от точки до прямой равно перпендикуляру, опущенному из этой точки на прямую.
Определение расстояния от точки до прямой (отрезка)
Определение расстояния от точки до прямой (отрезка)
Определение расстояния от точки до прямой (отрезка)
Определение длины средней линии треугольника и трапеции Что нужно вспомнить: Средняя линия треугольника параллельна третей стороне и равна её половине; Средняя линия трапеции равна полусумме оснований.
Определение длины средней линии треугольника и трапеции
Определение длины средней линии треугольника и трапеции
Определение длины большего катета, большей диагонали Что нужно вспомнить: Стороны прямоугольного треугольника: катеты – образуют прямой угол: гипотенуза – лежит напротив прямого угла. Диагональ – отрезок соединяющий две не соседние вершины.
Задача 1 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета. Решение: По рисунку видно, что длина большего катета = 6. Ответ: 6. Определение длины большего катета, большей диагонали
Задача 2 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. Решение: По рисунку видно, что длина большей диагонали = 6. Ответ: 6. Определение длины большего катета, большей диагонали
Определение площади сложных или составных фигур
Задача 1 На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. Решение: Посчитаем количество клеток внутри закрашенной области: их 19 Ответ: 19. Определение площади сложных или составных фигур
Определение площади сложных или составных фигур
Определение градусной меры вписанного угла Что нужно вспомнить: Вписанный угол – угол, вершина которого лежит на окружности, а стороны её пересекают. Центральный угол – угол, вершина которого совпадает с центром окружности, а стороны её пересекают. Вписанный угол равен половине дуги, на которую опирается.
Задача 1: Найдите угол ABC. Ответ дайте в градусах. Решение: Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°. Ответ: 45. Определение градусной меры вписанного угла
Определение градусной меры вписанного угла
Определение градусной меры вписанного угла
Определение градусной меры вписанного угла
Использованы источники: Открытый банк заданий ОГЭ http://oge.fipi.ru Решу ОГЭ Математика http://oge.sdamgia.ru
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 679 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 302 человека из 66 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 508 115 материалов в базе
Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.
Другие материалы
- 21.02.2020
- 108
- 2
- 19.02.2020
- 211
- 5
- 19.02.2020
- 172
- 1
- 19.02.2020
- 260
- 8
- 17.02.2020
- 197
- 1
- 13.02.2020
- 250
- 0
- 12.02.2020
- 490
- 1
- 12.02.2020
- 152
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 21.02.2020 28172
- RAR 4.2 мбайт
- 266 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Безклейная Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 11 месяцев
- Подписчики: 5
- Всего просмотров: 34143
- Всего материалов: 3
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Школы Москвы будут самостоятельно принимать решение о длительности карантина
Время чтения: 1 минута
Школы Пскова перевели на дистанционное обучение
Время чтения: 2 минуты
Половина российских родителей не одобряют увлечение их детей просмотром видеоблогов
Время чтения: 2 минуты
В Тюменской области школы и колледжи перевели на дистанционное обучение
Время чтения: 1 минута
Все школы Оренбурга переводят на дистанционное обучение с 28 января
Время чтения: 1 минута
В Петербурге открыли памятник работавшим во время блокады учителям
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
Онлайн калькулятор. Модуль вектора. Длина вектора
Этот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал.
Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать
Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам
Размерность вектора:
Форма представления вектора:
Инструкция использования калькулятора для вычисления длины вектора
Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел..
Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Видео:Нахождение длины вектора. Практическая часть. 9 класс.Скачать
Вычисления длины вектора (модуля вектора)
Например, для вектора a = <ax; ay; az> длина вектора вычисляется cледующим образом:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Самый простой способ нахождения площадиСкачать
Длина вектора — основные формулы
Время чтения: 16 минут
Видео:Длина вектора через координаты. 9 класс.Скачать
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Видео:ОГЭ по математике На клетчатой бумаге с размером 1х1 изображен параллелограммСкачать
Как найти длину вектора
Модуль вектора а будем обозначать 
.
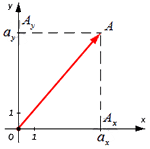
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор 
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
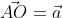
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора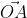 
получаем
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор дан в формате разложения по координатным векторам 
, то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.
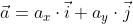
Чтобы рассчитать длину = (3, √x), расположенного в прямоугольной системе координат.
Чтобы найти модуль вектора используем ранее приведённую формулу
Ответ: 
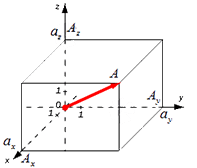
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор =(aₓ ; aᵧ ; a 
)
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
Ответ: 
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор 
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
При этом формула вычисления длины вектора для трёхмерного пространства, с координатами 
и 
), будет следующей:
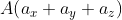
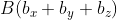
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
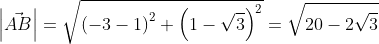
Существует второй вариант решения, где формулы применяются по очереди:
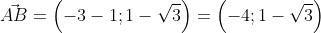
Ответ: 
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt)
(=sqrt = sqrt)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt=sqrt )
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Видео:егэ векторы решу егэ все задания №2 профильСкачать
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac ) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac)
(=2^2+4^2-2cdot2cdot4cdotcosfrac)
(=4+16-16cosfrac)
(=20-8=12 )
Получается (KM=sqrt )
Ответ: ( left|overrightarrowright|=sqrt )
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Видео:Угол между векторами | МатематикаСкачать
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
📽️ Видео
Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать
На клетчатой бумаге с размером клетки 1 × 1 изображена ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
Равенство векторов, Длина вектора.Как найти длину вектора?Скачать
Модуль вектора. Длина вектора.Скачать
МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать
