Имеет центр симметрии произвольная трапеция пара параллельных прямых параллелограмм (5 видео)

Геометрия. 8 класс

Выберите правильный ответ.

Какая фигура не имеет центра симметрии?

Впишите правильный ответ.

Сколько осей симметрии у шестиугольника с равными сторонами и углами (см. рисунок)?

Установите соответствие между фигурой и наличием у неё оси симметрии.

Не имеет оси симметрии

Имеет ось симметрии

Впишите правильный ответ.

Сколько осей симметрии у квадрата?

Выберите правильный ответ.

На каком рисунке верно построен отрезок, симметричный отрезку АB, относительно точки О?

Имеет центр симметрии произвольная трапеция пара параллельных прямых параллелограмм

Выберите верные утверждения.

Известно, что точка O центр симметрии, при которой точки А симметрична точке А₁ точка В симметрична точке В₁.

OB в 2 раза меньше OA.

Треугольник АОВ – равнобедренный.

Треугольник АОВ – равносторонний.

Треугольники АОВ и А₁ОВ₁ равны по двум сторонам и углу между ними.

Выберите правильный ответ.

Сколько заглавных печатных гласных букв из русского алфавита имеют ось симметрии?

Содержание

Имеет центр симметрии произвольная трапеция пара параллельных прямых параллелограмм
Трапеция
Элементы трапеции
Виды трапеции
🎥 Видео

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Имеет центр симметрии произвольная трапеция пара параллельных прямых параллелограмм

Постройте центр симметрии следующих фигур:

б) двух равных углов (в каких случаях это возможно?);

в) двух равных окружностей (рассмотрите все случаи);

г) двух равных треугольников (в каких случаях они могут быть центрально симметричны?).

Решение . Ответ: б) Два равных угла центрально-симметричны, если их стороны — противоположно направленные лучи. в) Во всех случаях центр симметрии — середина отрезка, соединяющего центры этих окружностей. г) Два равных треугольника могут быть центрально-симметричны, если соответственные стороны этих треугольников параллельны и нет параллельного переноса, переводящего один в другой.

Через центр симметрии квадрата ABCD проведена прямая I, пересекающая сторону AB. Докажите, что сумма расстояний вершин B и C квадрата до прямой равна сумме расстояний вершин A и D до этой прямой.

На сторонах квадрата вне его построены квадраты. Докажите, что их центры симметрии являются вершинами квадрата.

Дан параллелограмм ABCD, точка M принадлежит стороне BC, точка N принадлежит стороне CD, O — центр симметрии параллелограмма. Проведены прямые МО и NO, пересекающие прямые AD и AB соответственно в точках Р и Q. Докажите, что точки М, N, Р и Q — вершины параллелограмма.

Докажите, что объединение данного треугольника и треугольника, ему симметричного относительно середины какой-либо его стороны, является параллелограммом.

Докажите, что каждый четырёхугольник, имеющий центр симметрии, — параллелограмм.

Решение . Ответ: Указание: диагонали четырёхугольника, имеющего центр симметрии, делятся им пополам.

Отрезок центрально-симметричен отрезку AB относительно центра O. Найдите площадь треугольника ABO, если площадь треугольника равна 17,5.

Решение . Ответ: 17,5.

Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны BC и AD в точках K и M соответственно. Докажите, что

Решение . Треугольники BOK и DOM равны по стороне и двум прилежащим к ней углам: поскольку диагонали параллелограмма точкой пересечения делятся пополам, как вертикальные, как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей BD. Из равенства треугольников следует равенство их сходственных сторон: Что и требовалось доказать.

Приведем другое решение.

Точка пересечения диагоналей является центром симметрии параллелограмма (Атанасян Л. С., Геометрия 7−9, п. 47). Поэтому треугольники OKB и OMD центрально симметричны относительно точки О и, следовательно, равны. Поэтому их стороны BK и DM равны. Что и требовалось доказать.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Трапеция

Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Элементы трапеции

Видео:Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

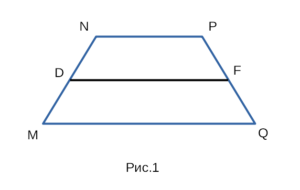
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.

В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.

Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.

Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.

Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.

Видео:Осевая симметрия. 6 класс.Скачать

Виды трапеции

Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.

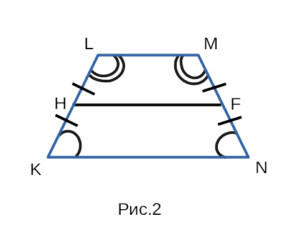
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.

В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.

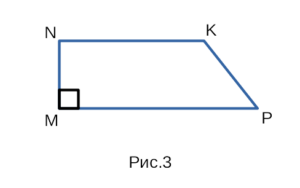
На рисунке 3 изображена прямоугольная трапеция MNKP, с боковыми сторонами MN и KP, с основаниями NK и MP, а также с прямым углом ∠NMP .

В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.