Наглядная геометрия, Рабочая тетрадь № 2, Смирнов В.А., Смирнова И.М., Ященко И.В., 2012.
Рабочие тетради «Наглядная геометрия» предназначены для учащихся средней школы. Они позволяют начать изучение геометрии в 5—б классах, ликвидировать пробелы в знаниях по геометрии в 7—8 классах, а в старших — подготовиться к ГИА и ЕГЭ.
Задачи, включенные в рабочие тетради, носят исследовательский характер и не требуют знания специальных формул и теорем. Они имеют различный уровень трудности, от простых до олимпиадных, и направлены на выявление математических способностей, развитие геометрических представлений и конструктивных умений учащихся.
Издание соответствует новому Федеральному государственному общеобразовательному стандарту.
Примеры.
Изобразите какой-нибудь равнобедренный треугольник, основанием которого является отрезок АВ, а вершина С находится в одном из узлов сетки.
Изобразите какой-нибудь четырехугольник, вершинами которого являются точки А, В, С и D. Сколько решений имеет задача?
Является ли шестиугольник, изображенный на рисунке, правильным?
На рисунке изображена замкнутая ломаная. Выясните, внутренней или внешней области принадлежат точки А, B, С.
Две фигуры F и F’ называются симметричными относительно точки О, если каждой точке одной фигуры соответствует симметричная точка другой фигуры. Точка О называется центром симметрии.
СОДЕРЖАНИЕ
Предисловие
1. Многоугольники и ломаные
2. Симметрия
3. Кривые как траектории движения точек
Ответы
1. Многоугольники и ломаные
2. Симметрия
3. Кривые как траектории движения точек.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Наглядная геометрия, Рабочая тетрадь № 2, Смирнов В.А., Смирнова И.М., Ященко И.В., 2012 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
Изобразите какой нибудь четырехугольник вершинами которого являются точки
Всякая простая замкнутая ломаная разбивает плоскость на две области — внутреннюю и внешнюю. На рисунке 16.1 внутренние области закрашены.
Фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью, называется многоугольникам. Вершины ломаной сторонами, — углами многоугольник а. Точки многоугольника, не принадлежащие его сторонам, называются внутренними.
Периметром многоугольника называется сумма длин всех его сторон.
Многоугольники подразделяются на треугольники — многоугольники с тремя углами (рис. 16.1, а), четырёхугольники — многоугольники с четырьмя углами (рис. 16.1, б) и т. д. Многоугольник, у которого п углов называется п-угольником.
Многоугольник называется правильным, если у него все стороны равны и все углы равны (рис. 16.2).
Правильный четырёхугольник называется также квадратом.
Прямоугольникам наз ывается ч етырёхугол ьник , у к оторого все углы прямые.
Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок (рис. 16.3).
Любой треугольник выпуклый. Среди многоугольников с числом углов, большим трёх, могут быть выпуклые (рис. 16.4, а) и невыпуклые (рис. 16.4, б).
Многоугольники могут иметь и более сложную формы. Примеры таких многоугольников показаны на рисунке 16.5.
Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины (рис. 16.6).
Ясно, что выпуклый многоугольник содержит все свои диагонали. Невыпуклый многоугольник может не содержать некоторые свои диагонали (рис. 16.6, б).
1. На сколько частей разбивает плоскость простая замкнутая ломаная?
2. Какая фигура называется многоугольником? Что называется:
а) вершинами; б) сторонами; в) углами многоугольника?
3. Какие точки многоугольника называются внутренними?
4. Что называется периметром многоугольника?
5. Какой многоугольник называется «-угольником?
6. Какой многоугольник называется: а) правильным; 6) выпуклым?
7. Что называется диагональю многоугольника?
8. Какой многоугольник содержит все свои диагонали?
1. Проверьте, что линия, изображённая на рисунке 16.7, является простой замкнутой ломаной. Выясните, какая из данных точек лежит:
а) внутри; 6) вне этой ломаной.
2. Укажите, какие из представленных на рисунке 16.8 фигур являются многоугольниками, а какие нет.
3. Укажите, какие из представленных на рисунке 16.9 фигур являются: а) выпуклыми многоугольниками; б) невыпуклыми многоугольниками.
4. Нарисуйте выпуклые и невыпуклые: а) четырёхугольник;
б) пятиугольник; в) шестиугольник. Используя линейку, найдите периметры этих многоугольников.
5. Нарисуйте правильные треугольник, четырёхугольник, пятиугольник и шестиугольник. Проверьте правильность нарисованных многоугольников с помощью линейки и транспортира.
6. Являются ли многоугольники, изображенные на рисунке 16.10, правильными?
7. На сколько треугольников делится выпуклый: а) четырёхугольник; 6) пятиугольник; в) шестиугольник своими диагоналями, проведёнными из одной вершины?
8. Сколько всего диагоналей имеет: а) четырёхугольник; б) пятиугольник; в) шестиугольник; г)* n-угольник?
9. Может ли многоугольник иметь: а) одну диагональ; б) три диагонали; в) восемь диагоналей; г) десять диагоналей; д) двадцать диагоналей?
10. Существует ли многоугольник: а) число диагоналей которого равно числу его сторон; б) число диагоналей которого меньше числа его сторон; в) число диагоналей которого больше числа его сторон?
11. Выпуклый многоугольник имеет 14 диагоналей. Сколько у него сторон?
12*. На клетчатой бумаге изобразите какой-нибудь четырёхугольник, вершинами которого являются точки АД С и D (рис. 16.11). Сколько таких четырёхугольников?
13. Изобразите два треугольника так, чтобы их общей частью был: а) треугольник; б) четырёхугольник; в) пятиугольник; г) шестиугольник.
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Четырехугольники. Наглядная геометрия.
Четырехугольники. Наглядная геометрия.
Просмотр содержимого документа
«Четырехугольники. Наглядная геометрия.»
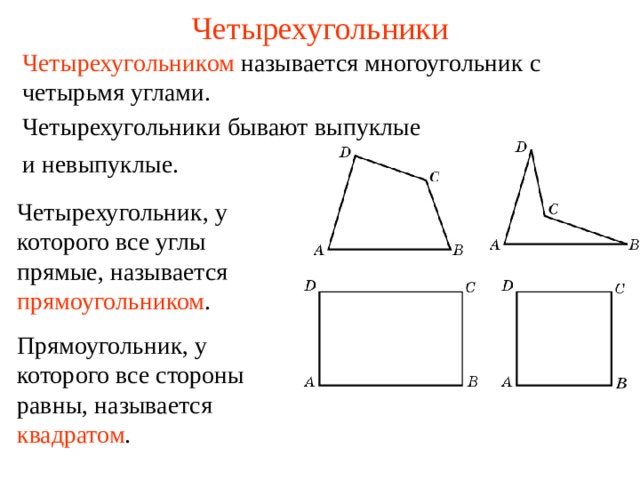
Четырехугольником называется многоугольник с четырьмя углами.
Четырехугольники бывают выпуклые
Четырехугольник, у которого все углы прямые, называется прямоугольником .
В режиме слайдов ответы появляются после кликанья мышкой
Прямоугольник, у которого все стороны равны, называется квадратом .
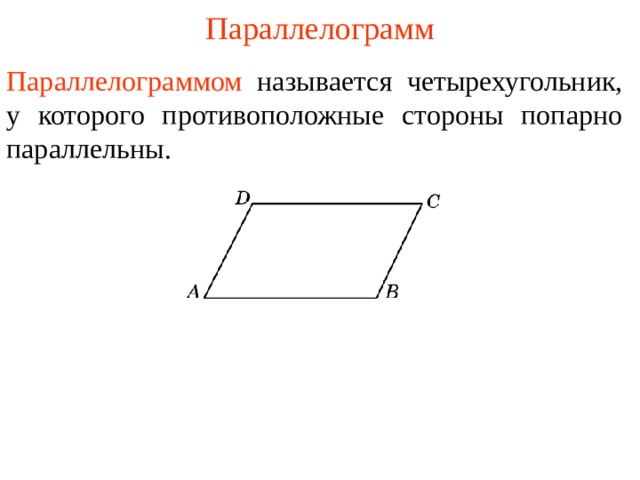
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны .
В режиме слайдов ответы появляются после кликанья мышкой
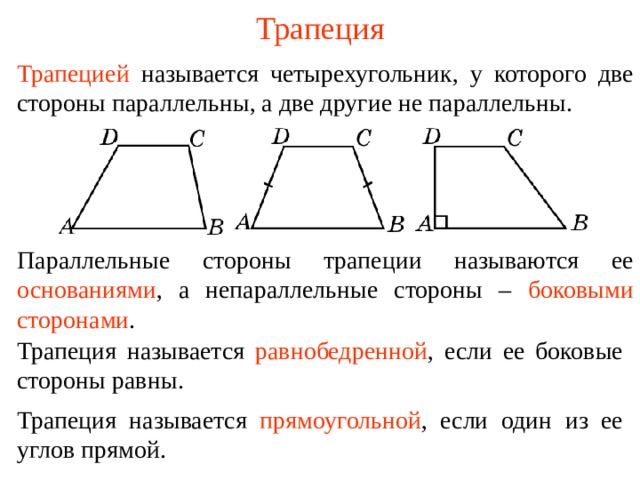
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называются ее основаниями , а непараллельные стороны – боковыми сторонами .
В режиме слайдов ответы появляются после кликанья мышкой
Трапеция называется равнобедренной , если ее боковые стороны равны .
Трапеция называется прямоугольной , если один из ее углов прямой .
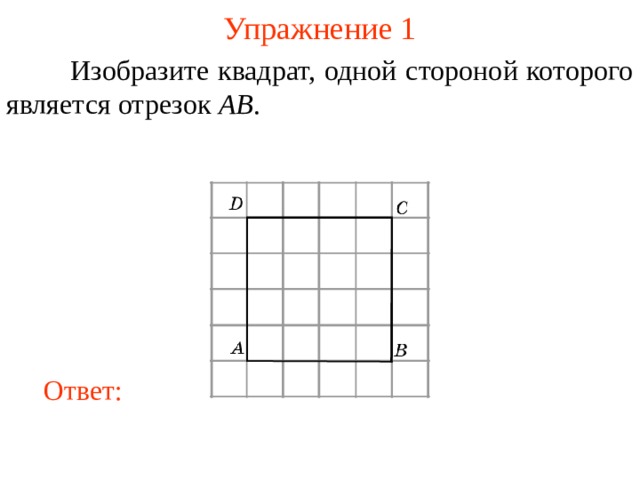
Изобразите квадрат, одной стороной которого является отрезок AB .
В режиме слайдов ответы появляются после кликанья мышкой
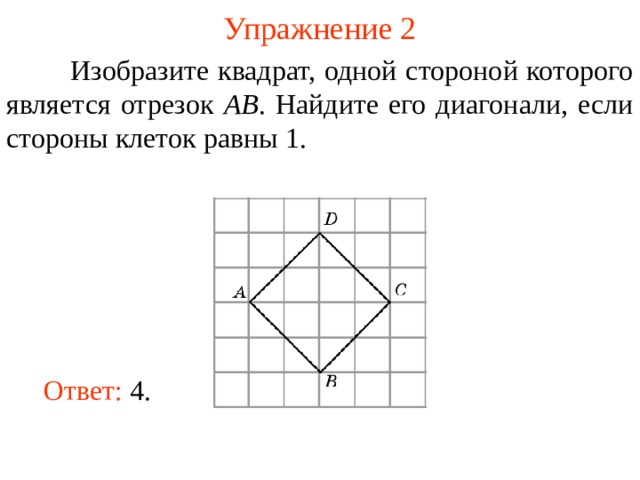
Изобразите квадрат, одной стороной которого является отрезок AB . Найдите его диагонали, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
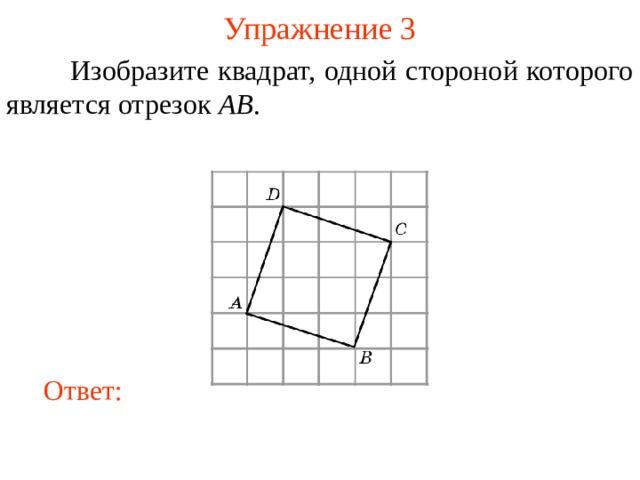
Изобразите квадрат, одной стороной которого является отрезок AB .
В режиме слайдов ответы появляются после кликанья мышкой
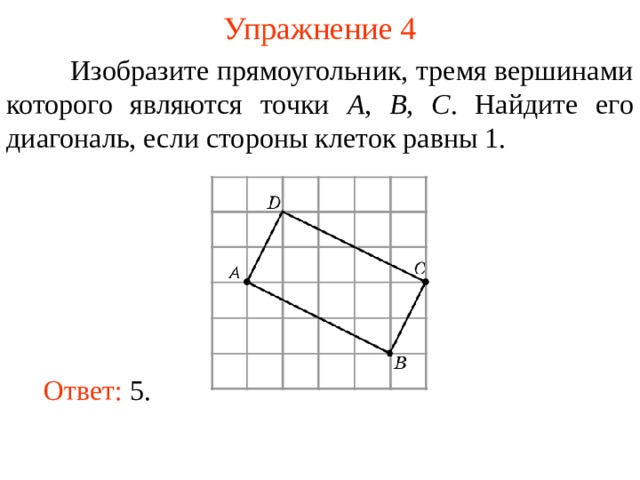
Изобразите прямоугольник, тремя вершинами которого являются точки A , B , C . Найдите его диагональ, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
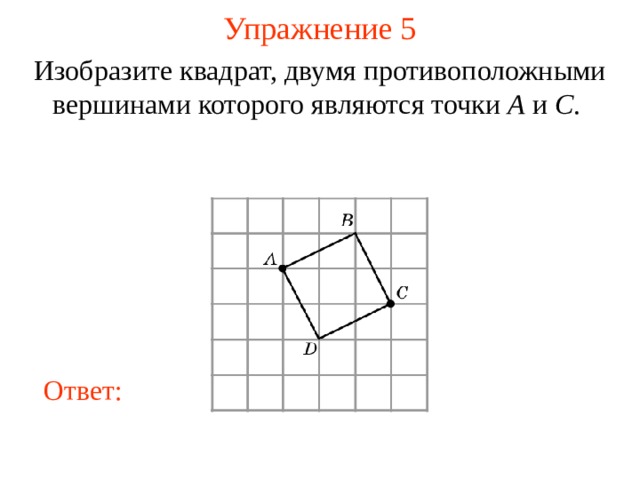
Изобразите квадрат, двумя противоположными вершинами которого являются точки A и C .
В режиме слайдов ответы появляются после кликанья мышкой
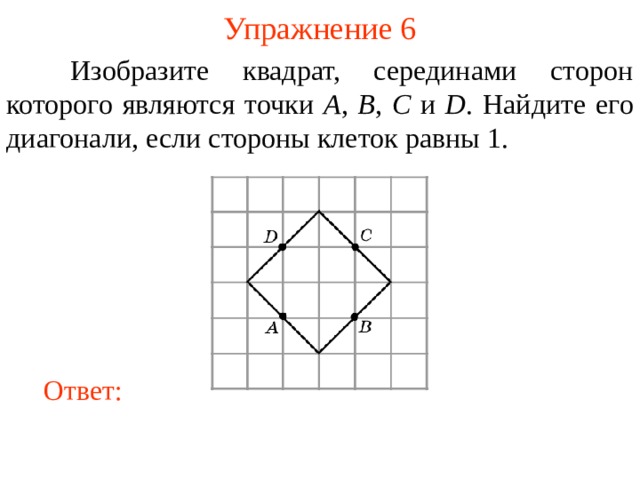
Изобразите квадрат, серединами сторон которого являются точки A , B , C и D . Найдите его диагонали, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
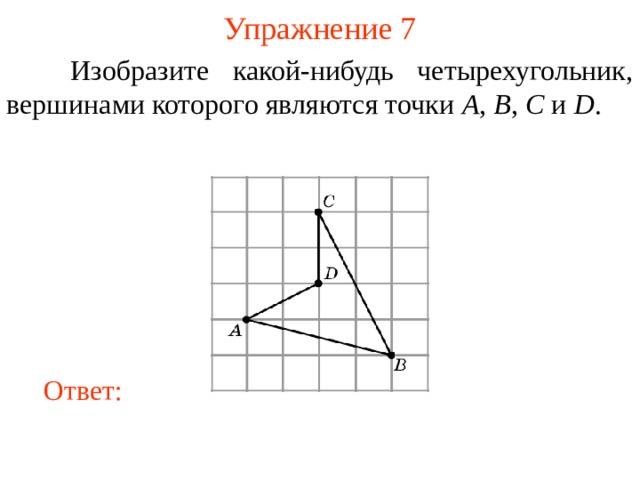
Изобразите какой-нибудь четырехугольник, вершинами которого являются точки A , B , C и D .
В режиме слайдов ответы появляются после кликанья мышкой
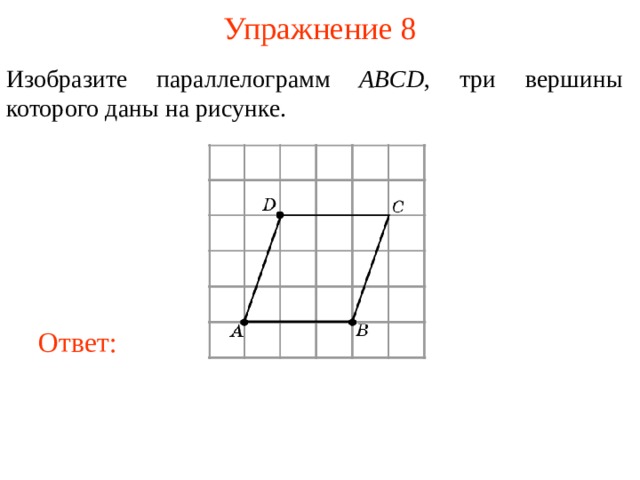
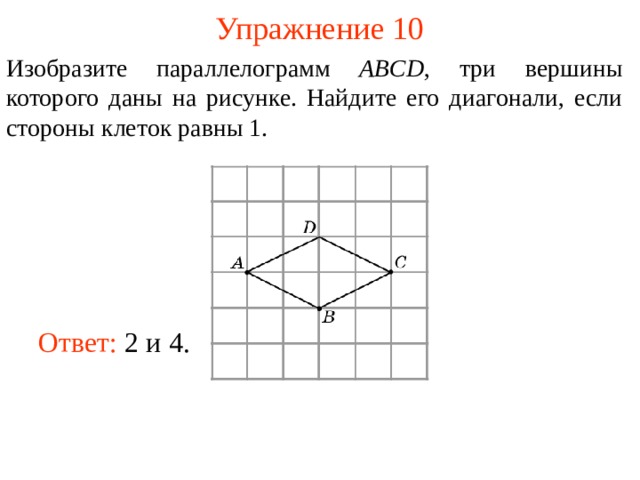
Изобразите параллелограмм ABCD , три вершины которого даны на рисунке.
В режиме слайдов ответы появляются после кликанья мышкой
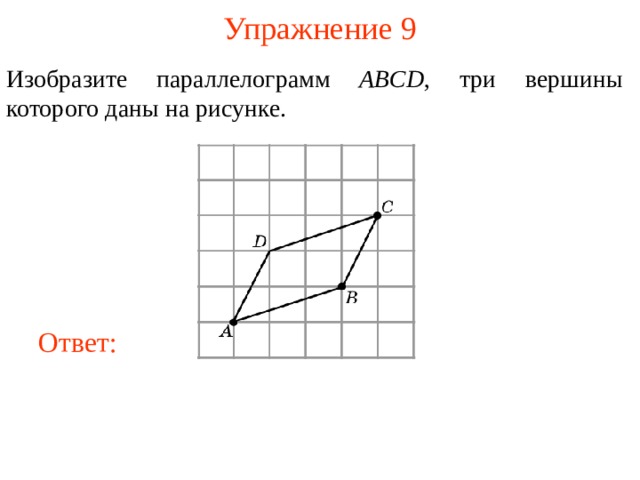
Изобразите параллелограмм ABCD , три вершины которого даны на рисунке.
В режиме слайдов ответы появляются после кликанья мышкой
Изобразите параллелограмм ABCD , три вершины которого даны на рисунке. Найдите его диагонали, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
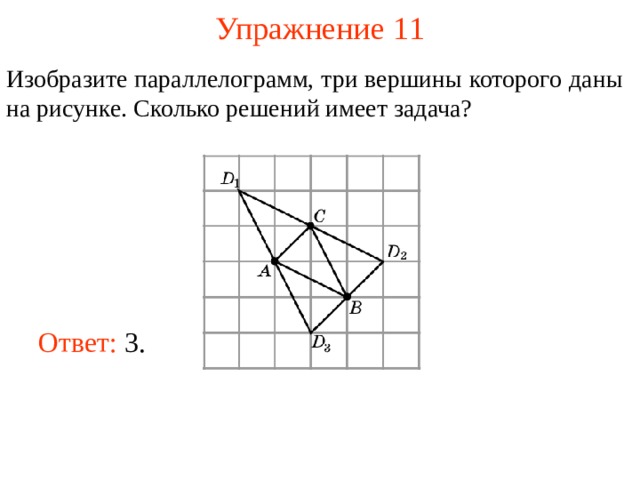
Изобразите параллелограмм, три вершины которого даны на рисунке. Сколько решений имеет задача?
В режиме слайдов ответы появляются после кликанья мышкой
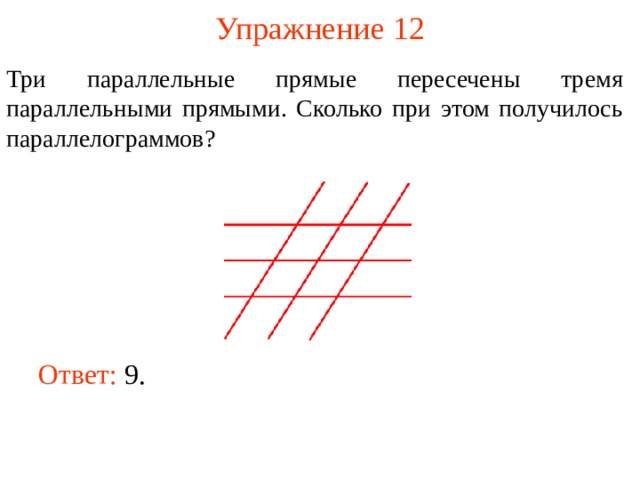
Три параллельные прямые пересечены тремя параллельными прямыми. Сколько при этом получилось параллелограммов?
В режиме слайдов ответы появляются после кликанья мышкой
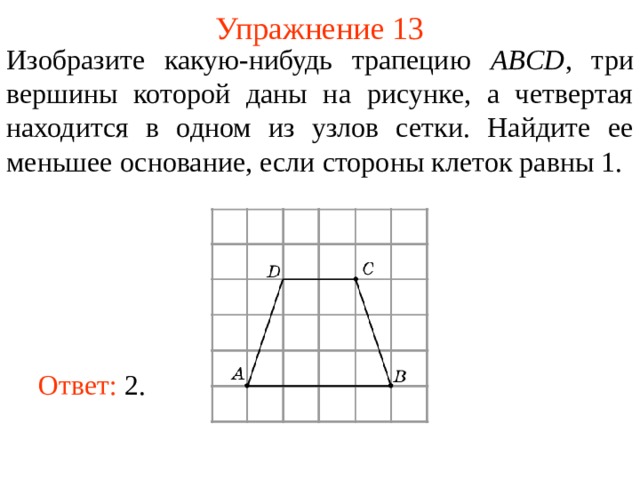
Изобразите какую-нибудь трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки. Найдите ее меньшее основание, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
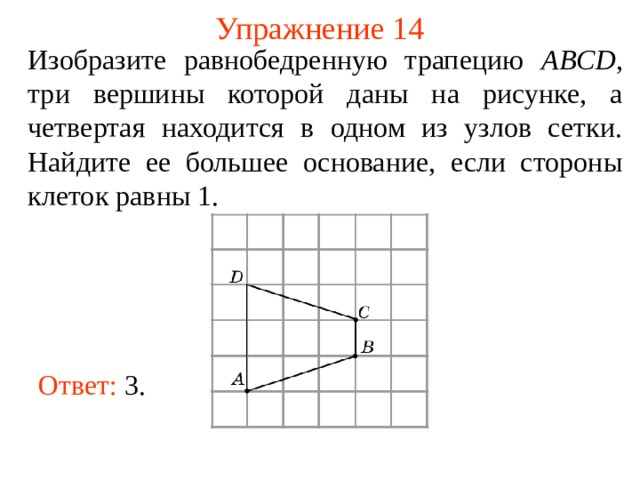
Изобразите равнобедренную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки. Найдите ее большее основание, если стороны клеток равны 1.
В режиме слайдов ответы появляются после кликанья мышкой
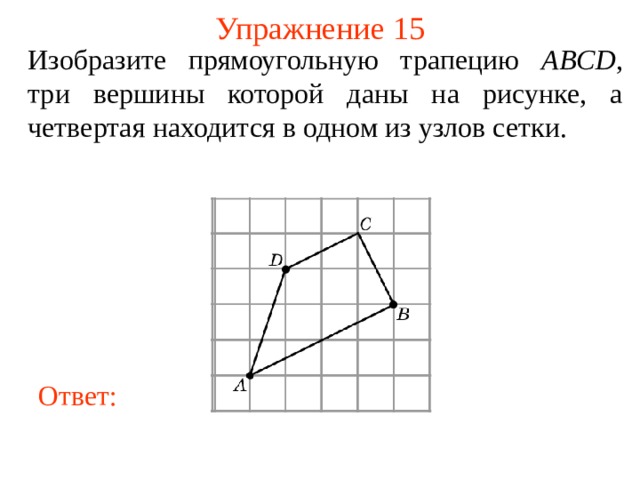
Изобразите прямоугольную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.
В режиме слайдов ответы появляются после кликанья мышкой
📺 Видео
ЕГЭ Математика Задание 6#27845Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

Как строить сечения параллелепипедаСкачать

8 класс. Геометрия. Четырехугольник: вершины, стороны, диагонали. Свойства параллелограмма. Урок #1Скачать

№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
8 класс, 3 урок, ЧетырехугольникСкачать

Геометрия Вершинами четырехугольника являются середины сторон ромба с диагоналями 8 см и 14 смСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

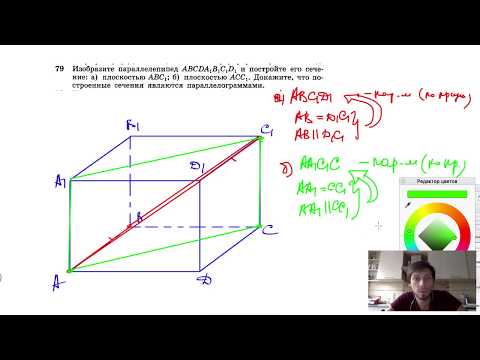
№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать

№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать