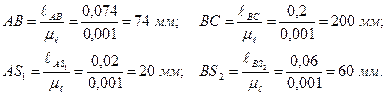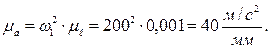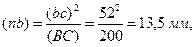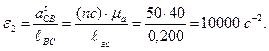Главный вектор сил инерции в равновесии звеньев отражает действие (8 видео)

ОПРЕДЕЛЕНИЕ СИЛ ИНЕРЦИИ В МЕХАНИЗМАХ

Силы инерции материальных точек звена могут быть приведены к одной точке и, таким образом, представлены их главным вектором и главным моментом.

Главный вектор сил инерции, называемый обычно силой инерции звена, равен

. (3.1)

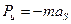
где m[кг] – масса звена, a_S[мсек -2 ] – ускорение центра S масс звена. Направление силы инерции P_и противоположно по направлению вектора a_S. Её размерность [кгмсек -2 ], т.е. она измеряется в ньютонах [Н].

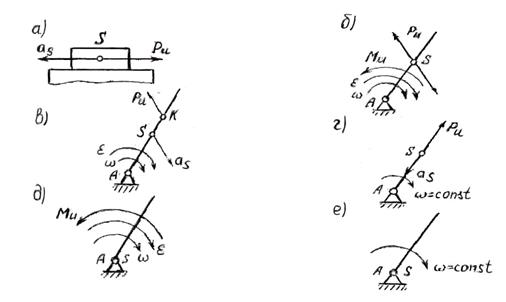
Мы ограничимся рассмотрением случаев, когда звено совершает плоскопараллельное движение и имеет плоскость материальной симметрии, параллельную плоскости его движения. При этом точкой приведения сил инерции звена целесообразно брать его центр масс (рисунок 3.1), так как упрощается выражение момента инерционной пары сил – главного момента сил инерции, что то же, инерционного момента. Он оказывается равным

, (3.2)

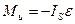
где I_S [кгм 2 ] – момент инерции масс звена относительно оси, проходящей через его центр масс перпендикулярно плоскости его материальной симметрии, или, иначе, центральный момент инерции звена, ε [сек -2 ] — угловое ускорение звена.

Инерционный момент М_и имеет размерность [кгмсек -2 ]=[Нм]. Плоскость, в которой он действует, параллельна плоскости движения звена; он направлен в сторону, противоположную направлению углового ускорения звена (рисунок 3.1).

Таким образом, в указанных выше случаях инерционная нагрузка звена представляется одной инерционной силой Р_и, приложенной в точке S и определяемой формулой (3.1), и одним инерционным моментом М_и, определяемым формулой (3.2).

Рисунок 3.1 – Инерционная нагрузка звена

Частные случаи инерционной нагрузки

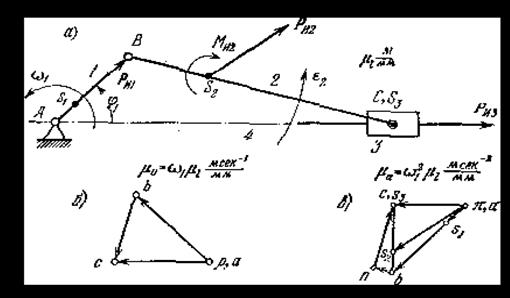
· Поступательное движение звена (рисунок 3.2, а). Инерционная нагрузка состоит из одной инерционной силы Р_и, определяемой формулой (3.1).

· Неравномерное вращательное движение звена (рисунок 3.2, б). Инерционная нагрузка состоит из силы инерции Р_и, определяемой формулой (3.1), и инерционного момента М_и, определяемого формулой (3.2). Модуль полного ускорения центра масс звена в этом случае равен

, (3.3)

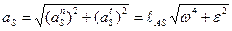
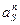
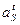
где и — нормальное (центростремительное ) и касательное (тангенциальное) ускорения центра масс звена, ω и ε – угловая скорость и угловое ускорение звена, ℓ_AS – расстояние от центра масс S до оси А вращения звена.

Силу Р_и и момент М_и можно привести к одной силе .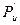

Для этого следует силу Р_и приложить, сохраняя ее направление, в центре К качания звена (рисунок 3.2, в). Расстояние ℓ_AK центра качания К звена от оси вращения последнего А равно

, (3.4)

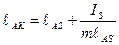
где I_S – центральный момент инерции звена, а m – его масса.

Рисунок 3.2 – Частные случаи инерционной нагрузки

· Равномерное вращательное движение звена (рисунок 3.2, г). Инерционная нагрузка состоит только из силы инерции Р_и звена, которая в этом случае направлена по линии AS противоположно направлению вектора центростремительного (нормального) ускорения центра масс звена. Это ускорение равно

, (3.5)

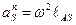
и, следовательно, центробежная сила инерции будет рана

. (3.6)

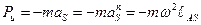
Произведение mℓ_AS называется неуравновешенностью или дисбалансом и имеет размерность [кг·м].

· Неравномерное вращательное движение звена при совпадении центра масс S звена с его осью вращения А (рисунок 3.2, д). В этом случае инерционная нагрузка звена состоит только из инерционного момента М_и, который находится по формуле (3.2).

· Равномерное вращательное движение звена при совпадении центра масс S звена с его центром вращения А (рис. 3.2, е). В этом случае ℓ_AS = 0 и в соответствии с формулой (3.3) a_S=0, следовательно, Р_и=0, и так как ε=0 (равномерное вращение), то М_и=0.

В этом случае инерционная нагрузка звена равна нулю и оно называется уравновешенным (следует помнить, что рассматривается плоская система сил).

Пример. Для кривошипно-ползунного механизма (рисунок 3.3) определить инерционную нагрузку всех звеньев.

Задачу решить для положения, когда угол φ=45 о .

Решение. 1). Построение схемы механизма (рисунок 3.3, а).

Рисунок 3.3 – Определение инерционной нагрузки звеньев

Задаемся масштабом чертежа μ_ℓ=0,001 м/мм и строим схему механизма. Чертежные длины звеньев определятся

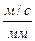
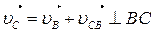
2). Построение плана скоростей(рисунок 3.3,б). Рассчитываем масштаб скорости в масштабе кривошипа.μ_υ = ω₁ μ_ℓ=200·0,001= 0,20 . Тогда длина вектора скорости υ_В, т.е. отрезок (Рb), будет равен (АВ)=(Рb)=74 мм. Точку “с” на плане скоростей находим по векторному уравнению

3). Построение плана ускорений(рисунок 3.3, в). Строим план ускорений в масштабе кривошипа

Тогда на плане ускорений отрезок (πb), изображающий вектор нормального ускорения точки В, будет равен (АВ)=(πb)=74 мм. Точку “с” находим по векторному уравнению

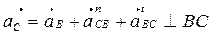
Отрезок (nb), изображающий на плане нормальное ускорение 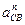, определится из равенства

где (bс)=52 мм – отрезок, замеренный с плана скоростей.

ТочкиS₁, S₂определим по правилу подобия, п.2. Но т.к. план ускорений построен в масштабе кривошипа, то (πs₁)=(AS₁)= 20 мм, (bs₂)=(BS₂)= 60 мм. Тогда ускорения центров масс определятся

Угловые ускорения находятся по формулам

Направление ε₂ будет против часовой стрелки в соответствие с направлением 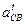тангенциального ускорения точки С звена ВС относительно точки В (рисунок 3.3, а).

4). Расчет инерционной нагрузкидля каждого звена.

а)Расчет инерционных сил.Сила инерции кривошипа равна

Вектор силы инерции приложен к центру масс кривошипа и направлен в противоположную сторону вектору ускорения a_S₁.

Сила инерции шатуна

Вектор силы инерции приложен к центру масс шатуна и направлен в противоположную сторону вектору ускорения a_S₂.

Сила инерции ползуна

Вектор силы инерции приложен к центру масс ползуна и направлен в противоположную сторону вектору ускорения a_С.

б)Расчет инерционных моментов. Для кривошипа инерционный момент равен М_и1=0, т.к. звено вращается равномерно.

Для шатуна инерционный момент определится по формуле

Этот момент направлен в противоположную сторону угловому ускорению.

Для ползуна момент инерции М_и3=0, т.к. звено движется поступательно.

Дата добавления: 2015-06-01 ; просмотров: 9924 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Занятие 7 - Силовой анализ кривошипно-кулисного механизмаСкачать

Силовой анализ механизмов

Читайте также:

A) анализ и самооценка собственных достижений
FMEA –анализа
I. Анализ конечных результатов нового учебного года
I. Анализ платежеспособности и ликвидности.
I. Анализ состояния туристской отрасли Республики Бурятия
I. Опровержение психоанализа
I. Предпосылки структурного анализа
I. Психоанализ как техника анализа ночной жизни
II. Анализ финансовой устойчивости.
II. Вывод и анализ кинетических уравнений 0-, 1-, 2-ого порядков. Методы определения порядка реакции
II. Дисперсионный анализ
II. Психоанализ как борец за интимную жизнь

104. «Активные» силы — это силы .

105. «Пассивные силы — это силы .

106.«Внутренние силы — это силы .

o взаимодействия звеньев

107. Обобщенная форма уравнения для расчета приведенного момента сил, приложенных к j —му звену, совершающему поступательное движение, имеет вид .

108.Мощность, затрачиваемая на преодоление сил трения в поступательной паре, рассчитывается по формуле .

109.Правильная последовательность силового расчета плоского механизма:

Силовой расчет начального звена 4
Разбивка кинематической цепи механизма на структурные группы Асура 2
Определение внешних сил, приложенных к звеньям механизма 1
Силовой расчет групп Асура 3

110.Вектор силы трения направлен противоположно вектору .

111.Направление вектора силы трения
… направлением вектора скорости

112.Силовой расчет механизмов с учетом сил инерции звеньев называют .

113.Уравновешивающая сила приложена к. звену механизма.

114.Кинетостатический метод расчета механизмов основан на учете сил и моментов . звеньев.

115.Учет сил трения приводит к отклонению силы взаимодействия звеньев от их общей нормали на угол, равный углу .

116.Величина неизвестной силы при силовом анализе механизма определяется методом рычага .

117.Полюс повернутого плана . при силовом анализе механизма по методу Жуковского используется в качестве рычага Жуковского.

118.Вектор силы трения направлен противоположно вектору .

119.Вектор силы трения направлен противоположно вектору .

120.Сила взаимодействия двух звеньев
при отсутствии трения направлена .

по нормали к их поверхности

121.Главный вектор сил инерции определяется из уравнения .

122. Главный вектор сил инерции в
уравнении равновесия механизма отражает действие .

ускоренного движения звеньев

123.Силовой расчет механизмов, учитывающий силы инерции звеньев, называют .

124.Силовой расчет механизма начинается с . звена

125.Сила, действующая на начальное
звено и обеспечивающая заданный за-
кон её движения, называется:

127.Параметры, определяемые при силовом расчете механизма,- это .

силы внутреннего взаимодействия звеньев

128.Уравновешивающая сила приложена к … звену механизма

129.Кинетостатический метод расчета механизмов основан на учете сил и моментов . звеньев

130.Сила взаимодействия звеньев при учете силы . отклоняется от их общей нормали на величину угла трения

131.Мощность, затрачиваемая на преодоление сил трения во вращательной паре, рассчитывается по формуле .

132.Реакцию взаимодействия звеньев во вращательной паре находят из соотношения .

133.Рычаг Жуковского используется для .

· определения величины неизвестной силы

134.Полюс повернутого плана . при силовом анализе механизма по методу Жуковского используется в качестве
рычага Жуковского

135.Использование рычага Жуковского при силовом анализе механизма предусматривает перенесение всех известных сил в одноименные точки повернутого плана скоростей .

· с сохранением направления сил

136.Приведенный момент инерции из меряется в .

137.Кинетостатический метод расчета механизмов основан на учете . . .

сил и моментов инерции звеньев

138. Звену, совершающему плоскопараллельное движение, соответствует инерционная нагрузка .

139.Звену, совершающему вращательное движение с ускорением, соответствует инерционная нагрузка .

140.Звену, совершающему поступательное движение, соответствует инерционная нагрузка .

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)

Видео:ЛЕКЦИЯ # 11. ТММ. Определение инерционных нагрузок. Определение реакций в кинематических парах.Скачать

Силовой анализ и уравновешивание механизмов

Силовой анализ механизмов

104.«Активные» силы — это силы .

105.«Пассивные силы — это силы .

o сопротивления среды

Читайте также:

Cпектральный анализ — способ определения химического состава вещества по его спектру.
E) биохимические анализы крови.
I. Дистрибутивный анализ. Дистрибутивная структура языка на фонемном уровне.
II. Метод синтаксического анализа по непосредственно составляющим.
II. Основные теории по анализу международных отношений.
II.1. Оценка финансовой деятельности строительной организации с помощью финансового анализа.
II.1.2.2. Анализ финансовой устойчивости предприятия
II.1.2.3. Анализ ликвидности
II.1.2.6. Анализ показателей рентабельности
II.1.2.Методика финансового анализа

106. «Внутренние силы — это силы . o взаимодействия звеньев

108.

Мощность, затрачиваемая на преодоление сил трения в поступательной паре, рассчитывается по формуле .

109.Правильная последовательность силового расчета плоского механизма:

0 Силовой расчет начального звена 4

0 Разбивка кинематической цепи механизма на структурные группы Асура 2

0 Определение внешних сил, приложенных к звеньям механизма 1

0 Силовой расчет групп Асура 3

110.Вектор силы трения направлен противоположно вектору .

111.Направление вектора силы трения
… направлением вектора скорости

112.Силовой расчет механизмов с учетом сил инерции звеньев называют .

113.Уравновешивающая сила приложена к. звену механизма.

114.Кинетостатический метод расчета механизмов основан на учете сил и моментов . звеньев.

116.Величина неизвестной силы при силовом анализе механизма определяется методом рычага .

118.Вектор силы трения направлен противоположно вектору .

119.Вектор силы трения направлен противоположно вектору .

оскорости

120.Сила взаимодействия двух звеньев
при отсутствии трения направлена .

опо нормали к их поверхности

121.Главный вектор сил инерции определяется из уравнения .

122. Главный вектор сил инерции в
уравнении равновесия механизма отражает действие .

o ускоренного движения

123.Силовой расчет механизмов, учитывающий силы инерции звеньев, называют .

124.Силовой расчет механизма начинается с . звена

125.Сила, действующая на начальное
звено и обеспечивающая заданный за-
кон её движения, называется:

127.Параметры, определяемые при силовом расчете механизма,- это .

осилы внутреннего взаимодействия звеньев

128.Уравновешивающая сила приложена к … звену механизма

оначальному

129.Кинетостатический метод расчета механизмов основан на учете сил и моментов . звеньев

оинерции

130.Сила взаимодействия звеньев при учете силы . отклоняется от их общей нормали на величину угла трения

131.Мощность, затрачиваемая на преодоление сил трения во вращательной паре, рассчитывается по формуле .

оN= F n *f*r*w

132.Реакцию взаимодействия звеньев во вращательной паре находят из соотношения .

133.Рычаг Жуковского используется для .

o определения величины неизвестной силы

о с сохранением направления сил

136.Приведенный момент инерции из меряется в .

137.Кинетостатический метод расчета механизмов основан на учете . . .

о сил и моментов инерции звеньев

138.

Звену, совершающему плоскопараллельное движение, соответствует инерционная нагрузка .

139.Звену, совершающему вращательное движение с ускорением, соответствует инерционная нагрузка .

140.Звену, совершающему поступательное движение, соответствует инерционная нагрузка .

Дата добавления: 2015-02-16 ; просмотров: 76 | Нарушение авторских прав

🎬 Видео

§4.3. Главный вектор и главный момент сил инерцииСкачать

Силовой анализ кривошипно-ползунного механизмаСкачать

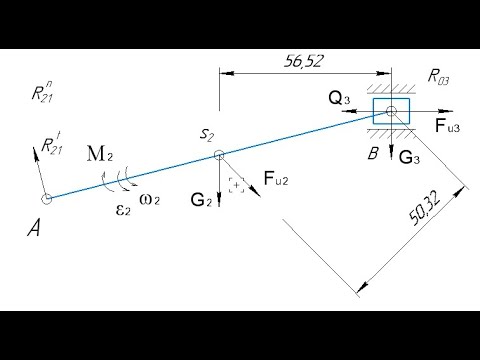
Теория механизмов и машин. Семинар по силовому расчёту: составление расчётной схемыСкачать

ЛЕКЦИЯ №14. ТММ. Силовой анализ механизма.Скачать

Теория механизмов и машин. Семинар по силовому расчёту: силовой расчёт по структурным группамСкачать

Сопротивление материалов. Лекция: косой изгиб и внецентренное растяжение-сжатиеСкачать

Формула строения механизма. Метод развития поводка. Общий алгоритм структурного анализа.Скачать

Расчет момента инерции тонкого стержняСкачать

Сопротивление материалов. Лекция: устойчивость сжатых стержней, часть 1Скачать

Прикладная механика Клссификация плоских механизмов по Ассур Артоболевскому Профессор АлимухамедоСкачать

Применение метода предельного равновесия для расчет на сейсмику (МРЗ)Скачать

Касумян А.О. - Сенсорные системы рыб - 7. Вестибулярная система (чувство равновесия)Скачать

Сопротивление материалов. Лекция: кручение тонкостенного профиляСкачать

Разбор структурного анализа плоского рычажного механизма. Разбиение механизма на группы Ассура.Скачать

9.2. Геометрические характеристики плоских сечений. Моменты инерции плоских сеченийСкачать

Сопротивление материалов. Лекция: кручение круглого стержняСкачать

Метод симметричных составляющих (виртуальная лаборатория РЗА - опыт 1)Скачать

Лира-САПР. Сопротивление материалов. Занятие 1. Определение геометрических характеристик сеченияСкачать