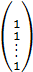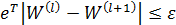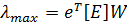Цель лабораторной работы
Знакомство с методами построения матрицы попарных сравнений и расчета ее собственного вектора.
Теоритическая часть
Матрицы парных сравнений
После построения иерархии устанавливается метод сравнения ее элементов. Если принимается метод попарного сравнения, то строится множество матриц парных сравнений. Для этого в иерархии выделяют элементы двух типов: элементы-«родители» и элементы-«потомки». Элементы-«потомки» воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами-«родителями». Матрицы парных сравнений строятся для всех элементов-«потомков», относящихся к соответствующему элементу-«родителю». Элементами-«родителями» могут являться элементы, принадлежащие любому иерархическому уровню, кроме последнего, на котором расположены, как правило, альтернативы. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы.
| Степень значимости | Определение | Объяснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия над другим (слабая значимость) | Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны | |
| Существенная или сильная значимость | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий | |
| Очевидная или очень сильная значимость | Убедительное свидетельство в пользу одного действия перед другим | |
| Абсолютная значимость | Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны | |
| 2,4,6,8 | Промежуточные значения между двумя соседними суждениями | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных выше ненулевых величин | Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение | Если согласованность была постулирована при получении N числовых значений для образования матрицы |
Таблица 2.1 — Шкала оценки сравнения альтернатив
Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент Е1 доминирует над элементом Е2 , то клетка матрицы, соответствующая строке Е1 и столбцу Е2, заполняется целым числом, а клетка, соответствующая строке E2 и столбцу Е1, заполняется обратным к нему числом. Если элемент Е2 доминирует над Е1 , то целое число ставится в клетку, соответствующую строке Е2 и столбцу Е1, а дробь проставляется в клетку, соответствующую строке Е1 и столбцу Е2. Если элементы Е1 и Е2 равнопредпочтительны, то в обе позиции матрицы ставятся единицы.
Для получения каждой матрицы эксперт или ЛПР выносит n(n-1)/2 суждений (здесь n — порядок матрицы парных сравнений).
Рассмотрим в общем виде пример формирования матрицы парных сравнений.
Пусть Е1, Е2, . Еn — множество из n элементов (альтернатив) и v1, v2, . vn — соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-«родителю»). В этом случае матрица парных сравнений [Е] имеет вид, изображенный в таблице 2.2.
| [E] = | E1 | E2 | . | En |
| E1 | v1/v1 | v1/v2 | . | v1/vn |
| E2 | v2/v1 | v2/v2 | . | v2/vn |
| . | . | . | . | . |
| En | vn/v1 | vn/v2 | . | vn/vn |
Таблица 2.2 — Общий вид матрицы парных сравнений
Матрица парных сравнений обладает свойством обратной симметрии, т. е.
При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.
При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более предпочтительна или более вероятна.
Собственные векторы и собственные значения матриц
Ранжирование элементов, анализируемых с использованием матрицы парных сравнений [Е], осуществляется на основании главных собственных векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W положительной квадратной матрицы [Е] проводится на основании равенства
где λmax — максимальное собственное значение матрицы [E].
Для положительной квадратной матрицы [Е] правый собственный вектор W, соответствующий максимальному собственному значению λmax, с точностью до постоянного сомножителя С можно вычислить по формуле
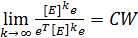
где е T — единичный вектор-строка = (1,1,…,1);
e — единичный вектор-столбец =
k = 1, 2, 3, . — показатель степени;
Вычисления собственного вектора W по выражению (2) производятся до достижения заданной точности:
где l — номер итерации, такой, что l = 1 соответствует k= 1; l = 2, k = 2;
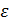
С достаточной для практики точностью можно принять 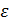
Умножение e T W – можно производить сложением всех элементов W
Максимальное собственное значение вычисляется по формуле:
Индивидуальное задание
Разработать программу, которая запрашивает число альтернатив, после этого, она последовательно задает вопросы о доминировании одной альтернативы, над другой, до тех пор, пока вся матрица не будет заполнена.
Описание разработанной программы:
Программа имеет консольный интерфейс. При запуске требуется ввести размерность матрицы попарных сравнений. В случае ввода недопустимого значения происходит завершение программы. После ввода размерности требуется последовательно ввести оценку для каждой пары альтернатив, располагающейся слева от главной диагонали (остальные значения будут вычислены на основе введённых данных). Если введённое значение недопустимо, пользователь должен повторить ввод для этой пары альтернатив. После ввода всех значений на экран выводится матрица попарных сравнений. Далее в консоль выводится собственный вектор полученной матрицы, после чего программа просит нажать клавишу Escape для завершения программы.
Скриншоты
Исходный код программы
Ответы на контрольные вопросы
1. Матрица парных сравнений — это квадратная матрица, элементами которой являются оценки всех возможных пар альтернатив, которые подвергаются сравнению.
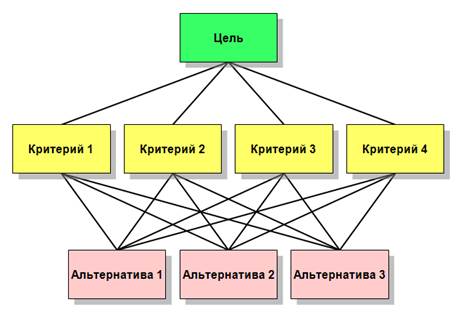
2. В методе парных сравнений существует иерархическая структура. Она изображена на рисунке 4.1. Элементы этой структуры и выступают по отношению друг к другу “родителями” и “потомками” в соответствии с их положением в иерархии.
Рисунок 4.1 — Иерархия в методе анализа альтернатив
3. Для заполнения матрицы ЛПР выносит n(n-1)/2 суждений (здесь n — порядок матрицы парных сравнений). Каждое суждение может принимать значения, указанные в таблице 2.1. С помощью этих суждений и обратных им суждений и происходит заполнение квадратной матрицы парных сравнений.
4. Вычисление главного собственного вектора W производятся по выражению 2.2.
5. Степень значимости отражает отношение двух альтернатив. Если степень значимости больше 1 — первая альтернатива предпочтительнее, если меньше 1 — вторая альтернатива предпочтительнее, если равна 1 — альтернативы имеют одинаковую значимость. Подробно степени значимости описаны в таблице 2.1.
Выводы
В ходе выполнения работы были изучены методы построения матрицы попарных сравнений и расчёта её собственного вектора. Эти методы были реализованы в консольной программе, написаной на ЯП Java. Данная программа запрашивает размерность n матрицы, а также запрашивает ввод n(n-1)/2 степеней значимости альтернатив, а на выходе выдаёт вектор полученной матрицы. Также программа корректно обрабатывает ошибки, связанные со вводом недопустимых данных.
Видео:Собственные векторы и собственные значения матрицыСкачать

Расчет векторов приоритетов как собственных векторов матриц парных сравнений
Вычисление главного собственного вектора W положительной квадратной матрицы А проводится на основании равенства
где А.тах — максимальное собственное значение матрицы А; Е — единичная матрица того же размера п х п.
Но во многих источниках (как в учебниках, так и в интернет-ресурсах [1] ) для практического отыскания вектора приоритетов рекомендуют приближенную формулу
согласно которой каждую компоненту вектора W находят как среднее гео- метрическое элементов соответствующей строки матрицы А. Заметим, что эта формула точна для матриц размера и=3и служит достаточно точным приближением для матриц А большего размера, если они хорошо согласованы, т.е. с достаточной точностью выполнено свойство однородности aik = = ajs? ask. Однако при плохой согласованности матрицы А формула (11.3) может давать ошибочные результаты уже для п = 4. Убедимся в этом на примере.
Пример: метод средних геометрических для нахождения приоритетов.
Пусть имеются четыре альтернативы х,, х.„ х3, х4, и суждения эксперта о сравнении альтернатив по некоторому критерию представлены в виде матрицы парных сравнений А
Требуется найти вектор приоритетов IT двумя способами:
- а) методом геометрических средних;
- б) через главный собственный вектор матрицы парных сравнений А. Для большей убедительности результатов два значения в матрице парных сравнений А выбраны за пределами 10-балльной шкалы.
Для решения первым способом, применяя соотношение (11.3), получим компоненты приближенного вектора по формуле геометрических средних
Для сопоставления с точным результатом выполним нормировку вектора, разделив каждую из величии Wk на сумму всех четырех компонент. Получим компоненты нормированного приближенного вектора IT: IT, = 0,308, 1Т2 = 0,244, IT., = 0,275,1Т4 = 0,173. Формула (11.3) приводит к выводу об оптимальности альтернативы xv причем ближайшей конкурирующей альтернативой будет х,
Однако при точном нахождении главного собственного вектора, удовлетворяющего уравнению (11.2), компоненты нормированного вектора 1Т с точностью 0,001 оказываются равны IT, = 0,123, W2 = 0,462, VT3 = 0,207, IT, = 0,208. Таким образом, на самом деле оптимальной будет альтернатива х2, а ближайшей конкурирующей (с большим отрывом) — хЛ
Погрешность отыскания приоритетов первых двух альтернатив по формуле (11.3) в этом примере велика: в абсолютном выражении она составила 0,185 и 0,218, а в относительном — в 2,5 и в 2 раза. И главное — выводы на основе формулы (11.3) неверны.
Таким образом, рассмотренный пример приводит к следующему заключению.
Формула (11.3) расчета приоритетов как средних геометрических величин элементов матрицы А парных сравнений для п > 4 при плохой согласованности суждений в матрице А может давать высокие погрешности и неверные выводы относительно оптимальных альтернатив.
Учитывая возможность существенных ошибок при использовании формулы (11.3), приведем метод последовательного сколь угодно точного нахождения нормированного (имеющего сумму компонент, равную единице) главного собственного вектора W.
Наиболее точный и практически эффективный способ отыскания главного собственного вектора W матрицы А — с помощью пакетов прикладных математических программ. В частности, встроенные функции нахождения собственных чисел и векторов имеются во всех основных самых распространенных пакетах (Mathematica, MATLAB, Maple, MathCAD и др.).
При отсутствии доступа к специализированным математическим пакетам (например, при наличии только офисного табличного редактора Excel, не имеющего встроенной функции для поиска собственных чисел и векторов) главный собственный вектор можно найти с помощью последовательных приближений (как правило, за небольшое число шагов) на базе следующей теоремы.
Для положительной квадратной матрицы А нормированный правый собственный вектор W, соответствующий максимальному собственному значению Хтах, можно вычислить по формуле
где е — вектор, состоящий из п единиц; Т — знак транспонирования; k = 1,2,3. показатель степени (число итераций).
С достаточной для практики точностью можно принять ? = 0,01 независимо от порядка матрицы.
Одновременно с главным собственным вектором W можно найти и максимальное собственное значение А,шах, которое требуется для исследования согласованности матрицы парных сравнений А. Максимальное собственное значение вычисляется по формуле:
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Собственный вектор матрицы парных сравнений
Автор: Пользователь скрыл имя, 15 Марта 2012 в 18:00, реферат
Краткое описание
.математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению.
Файлы: 1 файл
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1.docx
1.математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение, какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант, который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским математиком Томасом Саати, который написал о нем книги, разработал программные продукты и в течение 20 лет проводит симпозиумы ISAHP. МАИ широко используется на практике и активно развивается учеными всего мира. В его основе наряду с математикой заложены и психологические аспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод Анализа Иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем в бизнесе, промышленности, здравоохранении и образовании. Для компьютерной поддержки МАИ существуют программные продукты, разработанные различными компаниями. Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки . Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.
2. Собственный вектор матрицы парных сравнений. Собственный вектор матрицы парных сравнений определяет порядок важности сравниваемых объектов в количественном выражении. Он обеспечивает упорядочение приоритетов (критериев) объектов. Иногда значения собственного вектора матрицы парных сравнений назы- вают вектором приоритетов, а собственное значение является мерой согласованности суждений.
Следующим шагом, после составления матрицы парных сравнений, является вычисление вектора приоритетов. Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице.
Метод отыскания вектора w основывается на одном из утверждений линейной алгеб-ры — искомый вектор является собственным вектором матрицы парных сравнений, со-ответствующим максимальному собственному числу — λmax. В этом случае отыски-вается λmax, а затем достаточно решить векторное уравнение A*w= λmax *w.
Процедура определения собственных векторов матриц поддается приближе-нию. Например, приближенное вычисление собственного вектора (столбца) методом среднего геометрического измерения расстояний между оцениваемыми объектами может быть осуществлен в следующем порядке:
— перемножаются элементы каждой строки и полученные результаты записы-ваются в столбец;
— извлекается корень n-й степени из каждого элемента найденного столбца;
— складываются элементы этого столбца;
— каждый из этих элементов делится на полученную сумму.
Тем самым получается нормализованный вектор приоритетов.
3. Оценка однородности суждений
В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина aij ни была взята для сравнения i-го элемента с j-м, aij приписывается значение обратной величины, т. е. аij = 1/aij. Отсюда следует, что если один элемент в а раз предпочтительнее другого, то последний только в 1/а раз предпочтительнее первого.
При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (OO) в соответствии со следующими выражениями:
где М(ИО) — среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл. 2.3), полученных в работе [2].
Среднее значение индекса однородности в зависимости от порядка матрицы
В качестве допустимого используется значение OO ≤ 0,10. Если для матрицы парных сравнений отношение однородности OO > 0,10, то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.
4. Иерархический анализ используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев (элементов), имеющих в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии. Ниже рассматривается алгоритм иерархического синтеза [9] с учетом обозначений, принятых в иерархии на рис.2.1.
На первом шаге определяются векторы приоритетов альтернатив ^^относительно элементов Kj предпоследнего уровня иерархии (i=S).
Здесь через Kj обозначены элементы иерархии (критерии), причем верхний индекс / — указывает уровень иерархии, а нижний индекс j — порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив Ws относительно S — уровня иерархии осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.5) и (2.6) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:
Ш а г 2. Аналогичным образом обрабатываются матрицы попарных сравнений собственно элементов Данные матрицы построены таким образом, чтобы определить предпочтительность элементов определенного иерархического уровня относительно элементов вышележащего уровня, с которыми они непосредственно связаны. Например, для вычисления векторов приоритетов элементов третьего иерархического уровня (см. рис. 2.1) обрабатываются следующие три матрицы попарных сравнений:
В матрицах через v обозначен вес, или интенсивность, Е -го элемента.
В результате обработки матриц попарных сравнений определяется множество векторов приоритетов элементов:
Полученные значения векторов используются впоследствии при определении векторов
приоритетов альтернатив относительно всех элементов иерархии.
Шаг 3. Осуществляется собственно иерархический синтез, заключающийся в последовательном
определении векторов приоритетов альтернатив относительно элементов Е находящихся на всех
иерархических уровнях, кроме предпоследнего, содержащего элементы Е . Вычисление векторов приоритетов проводится в направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащими различным уровням. Вычисление проводится путем перемножения соответствующих векторов и матриц.
Общий вид выражения для вычисления векторов приоритетов альтернатив определяется следующим образом:
где — вектор приоритетов альтернатив относительно элемента E1 , определяющий j-й столбец матрицы;
— вектор приоритетов элементов E1, связанных с элементом Ej вышележащего
Ниже приведен конкретный пример по вычислению векторов приоритетов альтернатив относительно элементов третьего (E³ ), второго (Е² ) и первого (Е¹ ) уровней иерархии с учетом конкретных связей между элементами иерархии (см. рис. 2.1).
Определение векторов приоритетов альтернатив для элементов второго уровня осуществляется
Результирующий вектор приоритетов альтернатив относительно корневой вершины иерархии Е¹1
вычисляется следующим образом:
Рассмотренная модификация МАИ может эффективно применяться при решении широкого класса
социально-экономических и управленческих задач.
🎬 Видео
7 4 Собственные векторы и собственные значенияСкачать

Метод парных сравненийСкачать

А.7.35 Собственные вектора и собственные значения матрицыСкачать

Метод парных сравнений - техникаСкачать

Собственные значения и собственные векторыСкачать

Собственные значения матрицыСкачать

Метод парного сравненияСкачать

Собственные значения и собственные векторы. ТемаСкачать

Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Собственные значения и собственные векторы. ПримерСкачать

7.1 Характеристический многочлен. Собственные векторы и подпространства IСкачать

Собственные числа матрицыСкачать

Линейная зависимость векторовСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать