Геодезия

Для студентов аспирантов и преподавателей

Содержание

Разделы
Основные методы создания государственной геодезической сети
Методы построения государственной геодезической сети
Основные методы построения государственной геодезической сети
Триангуляция
Полигонометрия
Трилатерация
Линейно-угловые геодезические сети
Комбинированные геодезические сети
Опорные сети из астрономических пунктов
Динамическая триангуляция
Спутниковые методы создания геодезических сетей
Радиоинтерферометрия со сверхдлинной базой (РСДБ)
2.3. Методы построения плановых опорных геодезических сетей
📺 Видео

Видео:Уравнивание измеренных углов в геодезическом четырехугольникеСкачать

Разделы

Сила тяжести и уровенные поверхности земли
Геоид и квазигеоид
Общий земной эллипсоид
Нормальная земля и фигура реальной земли
Референц-эллипсоид Красовского
Координаты и азимуты
Уклонения отвесных линий
Азимуты лапласа
Понятие о редукционной задаче
Геодезические сети и их назначение
Основной принцип построения геодезической сети
Плотность пунктов государственной
Необходимая точность построения ггс
Основные методы создания ггс
Сведения о других методах создания ггс
Опорные геодезические сети в дореволюционной России
Схема и программа Ф.Н. Красовского построение государственной триангуляции
Государственная геодезическая сеть в СССР
Последовательность выполнения основных геодезических работ
Пути cовершенствования ггс
Общие сведения о проектировании ггс
Рекогносцировка геодезических пунктов
Расчет высоты геодезических знаков
Геодезические знаки
Центры геодезических пунктов
Априорная оценка точности геодезических сетей
Определение веса измеряемых величин
Вычисление обратного веса уравненных элементов
Априорная оценка точности ггс с моделированием результатов измерений на компьютере
Оценка точности триангуляции
Оценка точности рядов и сетей трилатерации по приблеженным формулам
Оценка точности звеньев полигонометрии
Согласование точности измерения горизонтальных направлений, азимутов и длин сторон в геодезических сетях
Условия эксплуатации высокоточных теодолитов
Общие сведения о высокоточных теодолитах
Геометрическая схема высокоточного теодолита
Осевые системы и уровни теодолита
Лимб высокоточного оптического теодолита
Зрительные трубы высокоточных теодолитов
Отсчетное устройство оптического теодолита
Принцип совмещенного отсчета
Поверки и исследования высокоточных теодолитов
Определение рена оптического микрометра
Погрешности шкалы оптического микрометра
Определение эксцентриситета алидады и лимба
Отдельное спасибо
return_links(2); ?>

Видео:ЧАСТЬ 1. Экзаменационные задачи по инженерной геодезии для 1 курсаСкачать

Основные методы создания государственной геодезической сети

Согласно Инструкции основными методами построения государственной геодезической сети являются триангуляция, полигонометрия и трилатерация. Выбор того или иного метода в каждом конкретном случае определяется требуемой точностью построения сети и экономической эффективностью.

Метод триангуляции. Принято считать, что метод триангуляции впервые был предложен голландским ученым Снеллиусом в 1614 г. Этот метод широко применяется во всех странах. Сущность метода заключается в следующем. На командных высотах местности закрепляют систему геодезических пунктов, образующих сеть треугольников (рис. 13). В этой сети определяют координаты исходного пункта А, измеряют горизонтальные углы в каждом треугольнике, а также длины b и азимуты а базисных сторон, задающих масштаб и ориентировку сети по азимуту.

Сеть триангуляции может быть построена в виде отдельного ряда треугольников, системы рядов треугольников, а также в виде сплошной сети треугольников. Элементами сети триангуляции могут служить не только треугольники, но и более сложные фигуры: геодезические четырехугольники и центральные системы.

Основными достоинствами метода триангуляции являются его оперативность и возможность использования в разнообразных физико-географических условиях; большое число избыточных измерений в сети, позволяющих непосредственно в поле осуществлять надежный контроль всех измеренных величин; высокая точность определения взаимного положения смежных пунктов в сети, особенно сплошной. Метод триангуляции получил наибольшее распространение при построении государственных геодезических сетей.

Рис. 13. Сеть триангуляции

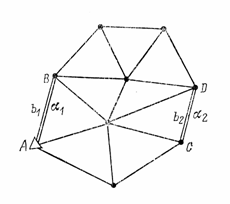
Рис. 14. Полигонометрический ход

Метод полигонометрии. Этот метод известен также давно, однако применение его при создании государственной геодезической сети сдерживалось до недавнего времени трудоемкостью линейных измерений, выполняемых ранее с помощью инварных проволок. Начиная примерно с шестидесятых годов текущего столетия, одновременно с внедрением в геодезическое производство точных свето и радиодальномеров, метод полигонометрии получил дальнейшее развитие и стал широко применяться при создании геодезических сетей.

Сущность этого метода состоит в следующем. На местности закрепляют систему геодезических пунктов, образующих вытянутый одиночный ход (рис. 14) или систему пересекающихся ходов, образующих сплошную сеть. Между смежными пунктами хода измеряют длины сторон s,-, а на пунктах — углы поворота р. Азимутальное ориентирование полигонометрического хода осуществляют с помощью азимутов, определяемых или заданных, как правило, на конечных пунктах его, измеряя при этом примычные углы у. Иногда прокладывают полигонометрические ходы между пунктами с заданными координатами геодезической сети более высокого класса точности.

Метод полигонометрии в ряде случаев, например, в залесенной местности, на территории крупных городов и т. п. оказывается более оперативным и более экономичным, чем метод триангуляции. Это обусловлено тем, что в таких условиях на пунктах триангуляции строят более высокие геодезические знаки, чем на пунктах полигонометрии, поскольку в первом случае следует обеспечить прямую видимость между гораздо большим числом пунктов, чем во втором. Постройка ,же геодезических знаков является самым дорогостоящим видом работ при создании геодезической сети (в среднем 50—60 % всех затрат).

Следует отметить также присущие методу полигонометрии недостатки:

сети полигонометрии, особенно одиночные ходы, являются гораздо менее жесткими геометрическими построениями, чем сети и ряды триангуляции, так как в полигонометрии число геометрических связей между пунктами существенно меньше, чем в триангуляции (при одинаковом числе пунктов в обоих случаях) ;

число избыточных измерений, а следовательно, и число условных уравнений, в полигонометрии гораздо меньше, чем в триангуляции с таким же числом пунктов, а это значит, что при прочих равных условиях сеть полигонометрии будет менее точной, чем сеть триангуляции;

контроль полевых измерений в полигонометрии несравненно хуже, чем в триангуляции, так как число условных уравнений в полигонометрии гораздо₁ меньше, чем в триангуляции с таким же числом пунктов.

Это свидетельствует о том, что при создании опорных геодезических сетей высшего класса точности возможности метода полигонометрии по сравнению с таковыми в триангуляции ограничены.

При создании же геодезических сетей последующих классов метод полигонометрии в силу присущей ему оперативности, особенно при использовании современных свето- и радиодальномеров с цифровой индикацией результатов измерений, получил широкое применение.

Метод трилатерации. Данный метод, как и метод триангуляции, предусматривает создание на местности геодезических сетей либо в виде цепочки треугольников, геодезических четырехугольников и центральных систем, либо в виде сплошных сетей треугольников, в которых измеряются не углы, а длины сторон. В трилатерации, как и в триангуляции, для ориентирования сетей на местности должны быть определены азимуты ряда сторон.

По мере развития и повышения точности свето- и радиодальномерной техники измерений расстояний метод трилатерации постепенно приобретает все большее значение, особенно в практике инженерно-геодезических работ.

При создании государственных геодезических сетей 1—2 классов метод трилатерации в СССР не применяется. Это объясняется следующими причинами:

1. Контроль измерения расстояний и построения сетей трилатерации слишком слаб, а иногда и вовсе отсутствует, что недопустимо в точных геодезических построениях. В самом деле, например, в треугольнике с измеренными сторонами контроль измерения расстояний полностью отсутствует, так как при таких измерениях в треугольнике не возникает ни одного условного уравнения; в геодезическом четырехугольнике и центральной системе с измеренными сторонами возникает всего лишь по одному условному уравнению, в то время как в таких же фигурах триангуляции с измеренными углами возникает во много раз больше независимых условных уравнений: в геодезическом четырехугольнике четыре, а в центральной системе еще больше.

2. В технико-экономическом отношении метод трилатерации также уступает методу триангуляции. При прочих равных условиях штат бригады при линейных измерениях и транспортные расходы в несколько раз больше, чем при угловых измерениях, поскольку приходится на конце каждой измеряемой с пункта линии устанавливать отражатель, а затем при переезде со светодальномером на другой пункт перевозить всех рабочих с отражателями с одних пунктов на другие, чего не требуется делать при угловых измерениях.

3. При соизмеримой точности угловых и линейных измерений точность передачи азимутов в рядах и сетях трилатерации существенно ниже, чем в сетях триангуляции.

Линейно-угловые геодезические сети. Под линейно-угловой сетью понимают такую разновидность триангуляции или трилатерации, в которой одновременно измеряют как углы, так и стороны треугольников. В этой сети через определенное число треугольников должны определяться азимуты Лапласа, необходимые для ее ориентирования. Линейно-угловые сети строят только в тех случаях, когда требуется создать геодезическую сеть с максимально высокой точностью, так как затраты труда, средств и времени на ее создание гораздо большие, чем при построении аналогичной сети триангуляции или трилатерации. Для того чтобы при создании линейно-угловых сетей получить наибольший эффект от совместного использования угловых и линейных измерений необходимо, чтобы средняя квадратическая ошибка измерения направлений, выраженная в радианной мере m_Njp, была равна относительной средней квадратической ошибке измерения длин сторон m_S/S, т. е. чтобы при измерениях соблюдалось равенство.

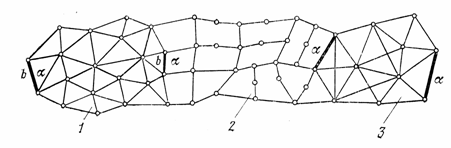
Рис. 15. Комбинированная геодезическая сеть: / — триангуляция; 2 — полигонометрия; 3 — трилатерация

Ошибки в обоих случаях должны вычисляться по свободным членам условных уравнений (по невязкам). При невыполнении этого равенства линейно-угловая сеть по сравнению с аналогичной сетью триангуляции или трилатерации не дает ощутимого выигрыша в точности.

Комбинированные геодезические сети. При выполнении геодезических работ встречаются случаи, когда значительные по площади участки того или иного района характеризуются либо резко различными формами рельефа (например, один участок— равнина, а соседний является горным), либо резко различным растительным покровом (например, один участок покрывают болота, заросшие травой и мелким кустарником, а на соседнем растет высокий хвойный лес) и т. д. В таких случаях по технико-экономическим соображениям на одном из участков (там, где это экономически более выгодно), геодезическую сеть (рис. 15) создают методом триангуляции, на другом — полигонометрии, на третьем — методом трилатерации и т. д. Другими словами, на территории района с резко различными условиями создают так называемую комбинированную геодезическую сеть.

Схема и методы построения комбинированных геодезических сетей могут быть разными и должны выбираться с учетом конкретных условий тех районов, в которых такие сети будут строить.

Методы построения государственной геодезической сети

Основные методы построения государственной геодезической сети

Основными методами построяния государственной геодезической сети являются триангуляция, полигонометрия, трилатерация и спутниковые координатные определения. Выбор конкретного метода определяется условиями местности, требуемой точностью и экономической эффективностью.

Триангуляция

Считают, что метод триангуляции предложен в 1614 г. Снеллиусом. На командных высотах устанавливают геодезические пункты, соединяя которые, получают треугольники ( рис. 1.3 ). В сети треугольников известными являются координаты пункта А, базис в и дирекционный угол а стороны АВ или координаты пунктов А и В. На пунктах триангуляции в треугольниках измеряют горизонтальные углы. Вычислив дирекционные углы и длины сторон треугольников, определяют координаты всех пунктов сети.

Полигонометрия

На местности строят геодезические пункты, которые соединяют между собой одиночным ходом или системой ходов, в которых измеряют длины сторон S i , соединяющие пункты, и на пунктах — углы поворота β i . Конечные пункты полигонометрии являются опорными, и на них измеряют примычные углы β 0 и β n между твердыми и определяемыми сторонами, для твердых сторон известны дирекционные углы или азимуты. В крупных городах, в залесенной местности и т. п. метод полигонометрии может быть более эффективным, так как требует менее высоких геодезических знаков, с которых нужно обеспечить видимость на гораздо меньшее число пунктов, чем в триангуляции и трилатерации (в среднем на постройку знаков приходится 50-60% всех затрат, их стоимость возрастает примерно пропорционально квадрату увеличения высот).

Недостатками полигонометрии по сравнению с триангуляцией являются: меньшая жесткость геометрического построения, меньшее число условных уравнений, слабый контроль полевых измерений, обеспечение узкой полосы местности.

Трилатерация

Трилатерация, как и триангуляция, состоит из цепочки треугольников, геодезических четырехугольников, центральных систем, сплошных сетей треугольников, в которых измеряют длины сторон. Исходными в трилатерации являются координаты одного или нескольких пунктов, а также дирекционные углы одной или нескольких сторон. Совершенствование и повышение точности свето- и радиодальномеров увеличивает роль трилатерации, особенно в инженерно-геодезических работах.

Линейно-угловые геодезические сети

В этих построениях измеряют углы и стороны треугольников, на некоторых линиях для ориентирования определяют азимуты Лапласа. Линейно-угловые сети создают для достижения максимальной точности определения координат пунктов, но они требуют гораздо больших затрат, чем триангуляция или трилатерация. Для достижения наибольшего эффекта угловых и линейных измерений целесообразно, чтобы m N /ρ = m s /s, где m s — средняя квадратическая ошибка измерения направления; р = 206 265″; m_s/s — относительная средняя квадратическая ошибка измерения длин сторон, причем m N и m s должны определяться по невязкам — свободным членам условных уравнений.

Комбинированные геодезические сети

Комбинированные геодезические сети создают на местности с сильно различающимися условиями, когда по технико-экономическим показателям целесообразно на одном участке создавать, например, триангуляцию, а на соседних — полигонометрию или трилатерацию.

Опорные сети из астрономических пунктов

Опорные сети из астрономических пунктов создают при топографических съемках масштаба 1:100 000 и мельче, пункты этой сети располагают на расстоянии 80-100 км. Для перехода к геодезическим широтам и долготам в астрономические координаты вводят поправки за уклонения отвесных линий, определяемые в первом приближении по данным гравиметрической съемки. Этот метод применялся в нашей стране более 40 лет назад при съемках масштаба 1:100 000 в горных районах северо-востока и Средней Азии, сейчас там построена высокоточная геодезическая сеть.

Динамическая триангуляция

Динамическая триангуляция предложена в 1920 г. финским геодезистом Вяйсяля. Суть ее сводится к синхронному наблюдению подвижных высоких целей m₁, m₂. m_n (воздушный шар, самолет и т. п.) с известных А, В и определяемых С, D пунктов ( рис. 1.4 )

Спутниковые методы создания геодезических сетей

Спутниковые методы создания геодезических сетей состоят из геометрических и динамических . В геометрическом методе ИСЗ используют как высокую визирную цель, в динамическом — ИСЗ является носителем координат. В геометрическом методе спутники фотографируют на фоне опорных звезд, что позволяет определить направления со станции слежения на спутники. Фотографирование нескольких положений ИСЗ с двух и более исходных и нескольких определяемых пунктов позволяет получить координаты определяемых пунктов. Эту же задачу решают путем измерения расстояния до спутников. Создание навигационных систем (в России — Глонасс и в США — Navstar), состоящих не менее чем из 18 ИСЗ, позволяет в любой момент в любой части Земли определять геоцентрические координаты X, Y, Z , с более высокой точностью, чем используемая ранее американская навигационная система Transit, которая позволяет определять координаты X, Y, Z, с ошибкой 3-5 м.

Радиоинтерферометрия со сверхдлинной базой (РСДБ)

Состоит из радиотелескопов А и В ( рис. 1.5 ), установленных на расстоянии D — базы интерферометра. Радиотелескопы синхронно принимают в сантиметровом диапазоне излучения одного и того же квазара К — внегалактического радиоисточника. Обработка записанных радиосигналов позволяет определить временную задержку моментов τ прихода фронта радиоволны к радиотелескопу А относительно В , а также частоту интерференции ƒ. Разность расстояний от радиотелескопов до квазара на момент наблюдения Δs = τΔ, где υ — скорость распространения радиоволн.

Видео:Системы координат в геодезииСкачать

2.3. Методы построения плановых опорных геодезических сетей

Известные способы триангуляции, трилатерации и полигонометрии, а также сочетания этих способов относятся к традиционным способам построения плановых опорных инженерно-геодезических сетей. Некоторые из этих способов, как, например, триангуляция сегодня утратили своё значение. Другие, как поли- гонометрия, наоборот, в связи с широким внедрением электронных тахеометров, наиболее востребованы, а в сочетании со спутниковыми определениями в настоящее время составляют основу методов и схем построения и сгущения инженерно-геодезических сетей.

Точность определения планово-высотного положения, плотность и условия закрепления пунктов (точек) геодезической основы должны удовлетворять требованиям производства крупномасштабных топографических съёмок, в том числе для разработки проектной и рабочей документации предприятий, сооружений, гражданских объектов. Кроме того, точность сетей должна быть достаточной для выноса проектов в натуру, выполнения специальных инженерно-геодезических работ, наблюдений за опасными природными и техногенными процессами, обеспечения строительства и эксплуатации объектов.

Технические требования к построению геодезической основы традиционными способами приведены в СП 47.13330.2012 и СГ1 11-104-97.

Для инженерных целей преимущественно развиваются сети 4 класса, 1 и иногда 2 разрядов, а на территориях больших городов могут строиться сети 2 и 3 классов с большими длинами сторон и более точными измерениями. Класс сети определяется площадью участка изысканий. Так, если площадь участка составляет от 25 до 50 км 2 и от 10 до 25 км 2 , то плановая опорная геодезическая сеть развивается построениями 4 класса, 1 и 2 разрядов. Высотные опорные сети для случая больших площадей строятся нивелированием III и IV классов; для меньших площадей нивелированием IV класса.

Если площадь участка изысканий заключена в пределах от 5 до 10 км , то плановая основа создаётся построениями 1 и иногда для целей внутриквартальных съёмок 2 разрядов; высотная основа—нивелированием IV класса. Для площадей менее 1 км опорные сети не предусмотрены, а только съёмочные сети. Съёмочные сети строятся теодолитными ходами или триангуляцией взамен теодолитных ходов. Высоты съёмочных сетей определяются техническим нивелированием независимо от площади съёмок.

В таблице 2.1. приведены характеристики точности классов построения инженерно-геодезической основы способами триангуляции, полигонометрии, три- латерации и линейно-угловыми построениями.

Высотная привязка центров пунктов опорной геодезической сети должна производиться нивелированием 111 и IV классов или техническим нивелированием, для которых предельные погрешности определения превышений на станции соответственно равны 2,6; 5,0 и 10,0 мм.

Триангуляция. Триангуляцией называют построенные на местности фигуры из треугольников, в которых измерены все углы и одна или, для целей контроля, две из сторон. Вершины треугольников закрепляют подземными центрами и обозначают наземными знаками — сигналами и пирамидами. В таких треугольниках по формулам тригонометрии легко находятся недостающие величины, что позволяет вычислять координаты вершин треугольников.

Триангуляционные сети используются в качестве основы для топографических съёмок, для производства разбивочных работ, а также для наблюдений за осадками и деформациями зданий и сооружений. В зависимости от назначения геодезической сети, размеров и формы объекта изысканий или строительства

Таблица 2.1. Характеристики точности классов построения инженерно-геодезических сетей

Плановая опорная геодезическая сеть, съёмочная сеть

Средняя квадратическая погрешность измерения углов, с

Предельная погрешность линейных измерений

форма триангуляционных построений, размеры сторон и точность измерений в триангуляционных сетях могут значительно различаться.

Некоторые типовые схемы простейших триангуляционных построений приведены на рис. 2.2. На рисунках измеренные стороны, называемые базисами, обозначены буквой Ь. В качестве исходных базисов и пунктов могут быть использованы стороны сетей более высокого класса (рис. 2.2, б, в).

Отличительной особенностью триангуляционных построений является минимальный объём линейных измерений, что являлось весьма весомым аргументом в пользу триангуляции во времена, когда электронные способы измерения расстояний ещё не были известны.

В таблице 2.2 приведены некоторые требования к развитию опорной инженерно-геодезической сети способом триангуляции для построений 4 класса 1 и 2 разрядов [33, 35].

Специальные инженерно-геодезические сети, построенные способом триангуляции (например, тоннельная триангуляция, гидротехническая триангуляция или мостовая триангуляция) имеют другие технические показатели, причём более жёсткие.

В соответствии с действующими нормативными документами основными показателями класса триангуляции являются средние квадратические ошибки измеренных углов trip, средние относительные ошибки наиболее слабых сторон mja и ошибки исходных сторон (базисов) т^Ь.

Для разбивочных сетей характерной особенностью является соблюдение заданной ошибки во взаимном положении соседних пунктов или пунктов, образующих опорную сторону для разбивочных работ. Такая специфика разбивочных сетей обусловлена тем, что с её пунктов производится разбивка точек, принадлежащих одному сооружению. Требования к взаимному положению точек некоторых сооружений могут быть достаточно жёсткими.

Рис. 2.2. Некоторые типовые схемы триангуляционных построений

Таблица 2.2. Некоторые характеристики построения опорных сетей способом триангуляции

Длина стороны треугольника, км

Число измеренных базисных сторон

Относительная средняя квадратическая ошибка, не более: Базисной стороны Стороны в наиболее слабом месте

1:200000
1:70000

1:50000
1:20000

1:20000
1:10000

Наименьшее значение угла треугольника в цепочке треугольников, градусов:

Предельная невязка в треугольнике, с

Средняя квадратическая ошибка измерения угла по невязкам в треугольниках, с, не более

Длина базисной стороны, км, не менее

Число треугольников между исходными (базисными) сторонами

Триангуляционная сеть 4 класса проектируется на карте, руководствуясь при этом нормативными требованиями СП. Сеть должна быть локальной, хотя отдельные её пункты могут быть совмещены с имеющимися на карте пунктами государственной сети, считая их пунктами более высокого класса.

Проектируя сеть на карте, следует руководствоваться тем положением, что наблюдения углов в сети будут выполняться со штатива на пирамиды высотой 6-8 м. Условия прохождения визирного луча между пунктами могут быть определены по профилям местности.

Выбор схемы или формы сети остаётся за проектировщиком в соответствии с условиями местности. Для территорий городов, населённых пунктов и строительных площадок могут оказаться целесообразными центральные системы или системы из треугольников, покрывающих весь участок.

В триангуляционной сети обязательно должно быть не менее двух исходных (базисных) сторон. В случае, если на участке имеется твёрдая сторона (между существующими пунктами), в проекте должно быть предусмотрено измерение ещё одной базисной стороны. Выполнение этих требований обеспечивает контроль масштаба сети. Для наглядности проект сети (в уменьшенном масштабе) отдельным рисунком изображается на отдельном листе бумаги (например, рис. 2.3). Для предварительной оценки проекта типичных схем построения сети можно пользоваться приближёнными формулами. Оценка в данном случае сводится к определению средней квадратической ошибки взаимного положения пунктов слабой стороны запроектированной сети. Слабой считается наиболее удалённая от обоих базисов сторона. При равенстве числа треугольников до разных сторон наиболее слабой будет сторона с наименьшей длиной.

На рис. 2.3 приведен ряд триангуляции (цепочка треугольников), опирающийся на две исходные базисные стороны Ь, и Ь₂. Стороны S,, S₂. общие для двух соседних треугольников, называют связующими, а противолежащие им углы А, В — связующими углами.

Рис. 2.3. Ряд триангуляции

Стороны S используются в последовательных вычислениях координат вершин треугольников, и проходящую но ним линию называют ходовой. Так сторона S, определится из соотношения

Для стороны S₂ будем иметь

В такой последовательности, решая треугольники, находят все стороны S ходовой линии.

Стороны сj, с₂ называют промежуточными, а противолежащие им углы С,, С₂ — промежуточными углами.

Средняя квадратическая ошибка связующей стороны цепочки, опирающейся на две исходные базисные стороны, может быть определена по известным приближённым формулам. Эти формулы основаны на сложении весов оцениваемой стороны. Веса определяются через среднюю квадратическую ошибку оцениваемой стороны. Ошибку вычисляют дважды: от начальной и конечной базисных сторон.

Если среднюю квадратическую ошибку стороны MF=S, полученную от базисной стороны Ь, обозначить через m_Sy а от базисной стороны Ь₂ — через m_S2, то соответствующие веса стороны 5 будут равны

Вес среднего значения длины стороны определится по формуле: а средняя квадратическая ошибка определяемой стороны 5 будет:

Средние квадратические ошибки m_s определяются но формуле

Эта формула записана в предположении, что т_м = m_Bi = щ_р и стороны в треугольниках приблизительно равны, т.е. S_< « S₂

— « 5 « » 6₂. Для сети в виде

центральной системы или геодезического четырёхугольника коэффициент перед S 2 будет равен 0,5.

Величина Y.(ctg 2 A_i + ctg 2 B_i + ctgA_j ctgBJ не зависит от точности измерений, а только от значений углов Л, и В,, г.е. от формы треугольников; её называют ошибкой геометрической связи или обратным весом треугольников и обозначают IR. Величины R табулированы и выбираются по связующим углам Л и В. Углы для этих целей измеряются транспортиром по схеме на карте. Также но карте определяют длины сторон. Если вычисления производятся для измерений по направлениям, то т_р = т,,-^2.

Ошибка исходной стороны т_ь практически всегда значительно меньше ошибок измерений развиваемой сети, хотя бы в два раза: т.е. т_ь/Ъ 171 q

Ошибку взаимного положения пунктов М и F находят из выражения

где первый член формулы отражает ошибку в длине стороны, а второй — ошибку её дирекционного угла, или, иначе, т 2 = m 2 _s + (m_a/p) 2 -L 2 .

Сказанное поясняет рис. 2.4.

Рис. 2.4. Ошибки угловых и линейных измерений

Исходя из принципа равных влияний ошибок угловых и линейных измерений, можно записать m_s = (m_a/p)-L, что позволит вычислить ошибку взаимного положения пунктов М и F но вычисленному значению m_s. Итак, т 2 = 2т. Найденное значение т сравнивают с допустимым. При удовлетворительном результате но принятому значению /л_р определяют класс сети и точность измерения базиса. В противном случае берут за основу другое значение /и_р, иначе говоря, назначают более высокий класс сети и расчёты повторяют.

Для оценки проекта сети на компьютере, имеющем соответствующую программу уравнивания (оценки) параметрическим способом, необходимо определить но карте или на схеме в масштабе в условной системе приближённые координаты всех пунктов. Как правило, во все программы для оценки проекта параметрическим способом необходимо ввести следующие данные:

• номер исходных точек и их координаты;
• среднюю квадратическую ошибку измеренного угла;
• приближённые координаты определяемых пунктов.

Обычно при оценке проектов принимают один из пунктов в качестве исходного, а координаты определяются но километровой сетке карты.

В результате оценки будут получены обратные веса функции определения координат всех пунктов и их средние квадратические ошибки по осям координат т_х и т_у Средняя квадратическая ошибка М планового положения пункта может быть приближённо подсчитана по формуле

Максимальное значение этой ошибки, соответствующее наиболее слабо определяемому пункту, сравнивается с допустимой величиной 2,5 см. Далее делается вывод и принимается соответствующее решение. Следует иметь в виду, что во многих программах заложена и оценка функции определения взаимного положения пунктов в наиболее слабо определяемом месте сети. Эту величину так же можно сравнить с допустимой и принимать соответствующее решение.

Основными достоинствами метода триангуляции являются его оперативность и возможность использования в разнообразных физико-географических условиях. Метод позволяет непосредственно в поле осуществлять контроль измеренных величин и с высокой точностью определять взаимное положения смежных пунктов сети.

Проектирование триангуляционных сетей выполняют на топографических картах 1:10000 и 1:25000 исходя из назначения сети, формы и площади территории, её рельефа и застроенности, наличия пунктов государственной сети и других параметров.

Рис. 2.5. Треугольник трилатерации

Способ трилатерации. Метод трилатерации, как и триангуляция предусматривает построение на местности геодезических сетей из треугольных фигур в виде цепочек треугольников, геодезических четырёхугольников и центральных систем, в которых измеряются не углы, а длины сторон. Сети трилатерации создаются для решения ряда инженерно-геодезических и специальных задач и строятся в виде свободных сетей, состоящих из отдельных типовых фигур и их комбинаций, или в виде сплошных сетей треугольников.

Базовой фигурой сети трилатерации является треугольник с измеренными сторонами а, Ь, с, см. рис. 2.5.

Длины сторон в фигурах трилатерации измеряются электронными тахеометрами и светодальномерами, а в сетях, создаваемых в качестве разбивочной основы, при строительстве зданий стороны измеряются компарированной рулеткой в 30 и 50 метров, что очень удобно на бетонной поверхности.

Необходимые нормативные требования к проектированию сети трилатерации 4 класса также выбираются из СП 11-104-97. Всё, что сказано применительно к триангуляции, относится и к сети трилатерации с учётом особенностей её построения. В таблице 2.3 приводятся основные требования к построению инженерно-геодезических сетей способом трилатерации [35].

Угол а в треугольнике трилатерации (см. рис. 2.5) может быть вычислен через

тригонометрические функции /gy или cos а по формулам:

Таблица 2.3. Основные требования к сетям трилатерации

Длина стороны треугольника, км

Относительная средняя квадратическая ошибка стороны

Наименьшее значение угла треугольника, град.

Число сторон между исходными сторонами, исходным пунктом и исходной стороной, не более

Количество приёмов измерения длин сторон электрооитическими дальномерами

Для линейно протяжённых объектов сеть трилатерации создают из цепочки треугольников или четырёхугольников.

Оценка проекта сети трилатерации может быть выполнена как на компьютере, при наличии соответствующей программы, так и при помощи приближённых формул для оценки точности типовых построений. В любом случае возникает необходимость в обозначении абсолютной ошибки измерения стороны сети. Для сетей 4 класса относительная средняя квадратическая ошибка измерения стороны должна быть не более 1:100000. Следовательно, абсолютная ошибка для разных длин сторон будет различной. В силу этого необходимо заранее определить рекомендуемый светодальномер или электронный тахеометр, обеспечивающий эту точность на минимальных длинах проектируемых линий.

Формулы для предварительной оценки точности проекта сети приведём для свободного ряда трилатерации [16]. Обозначим: m_s — средняя квадратическая ошибка измерения сторон ряда трилатерации; к — число треугольников от исходной стороны до оцениваемой связующей стороны; /У — среднее значение связующего угла ряда; М — ошибка взаимного положения двух пунктов связующей стороны к — го треугольника; т, — средний квадратический продольный сдвиг; т_и — средний квадратический поперечный сдвиг пунктов к — го треугольника. Тогда:

Расчёты по таким формулам для предварительного обоснования проектных решений достаточно эффективны в силу своей простоты и оперативности.

Средняя квадратическая ошибка вычисленного угла может быть найдена по формуле:

где т_а, т_ь и т_с — средние квадратические ошибки измерения сторон;

где И_а — высота треугольника, опущенная из вершины на сторону а.

Для линейно протяжённых объектов сеть трилатерации создают из цепочки треугольников. Одним из недостатков вытянутого ряда цепочки треугольников с измеренными сторонами является значительное превышение поперечного сдвига конечных точек ряда по отношению к продольному.

При оценке ожидаемой точности ряда равносторонних треугольников трилатерации используют формулы:

а) для продольного сдвига

где m_s — средняя квадратическая ошибка измерения сторон; N — число фигур ряда;

б) для поперечного сдвига:

где к — порядковый номер связующей стороны;

в) для дирекционного угла связующей стороны:

где S — длина стороны треугольников.

Недостатком сетей трилатерации из треугольников является также отсутствие полевого контроля качества измерений для каждой фигуры. Действительно, сумма вычисленных углов треугольника всегда будет равна 180° при любых ошибках измерения сторон, даже при грубых промахах. В связи с этим на практике взамен фигур из треугольников строят сети из геодезических четырёхугольников.

В каждом геодезическом четырёхугольнике измеряются две диагонали и все четыре стороны. Ясно, что одно из этих измерений является избыточным и может быть вычислено по результатам измерения других сторон. Это может служить полевым контролем качества измерений длин линий. Кроме того, геодезический четырёхугольник является более жёсткой фигурой, и ряд составленный из таких фигур, обладает более высокой точностью.

Оценка точности ряда геодезических четырёхугольников, состоящего из квадратов и уравненного за условия фигур, может быть выполнена но следующим формулам:

Наибольшее применение в практике инженерно-геодезических работ сети трилатерации получили при строительстве высотных зданий, дымовых труб, атомных и тепловых электростанций, а также при монтаже сложного технологического оборудования. В таких сетях высокую точность измерения длин сторон (до десятых долей миллиметра) обеспечивают, используя высокоточные свето- дальномеры, электронные тахеометры, инварные проволоки, а в некоторых случаях и жезлы специальной конструкции. Сети трилатерации с короткими сторонами называют сетями микротрилатерации.

Способ полигонометрии. Полигонометрией называют построенный на местности многоугольник, замкнутый или разомкнутый, в котором измерены все длины сторон и горизонтальные углы при вершинах. Вершины такого многоугольника закрепляются на местности специальными подземными знаками.

Инженерно-геодезические сети из нолигонометрических построений сегодня являются наиболее распространённым способом создания опорных плановых сетей, что обусловлено широким внедрением в геодезическое производство электронных тахеометров и светодальномеров.

Различают разомкнутые вытянутый и ломаный нолигонометрические ходы, которые опираются на исходные пункты и стороны с известными ди- рекционными углами.

В зависимости от площади объекта, его формы, обеспеченности исходными пунктами полигонометрия проектируется в виде одиночных ходов, системы ходов с узловыми точками или в виде замкнутых полигонов.

В практике инженерно-геодезических работ наибольшее применение нашли полигонометрические сети из ходов 4 класса, 1 и 2 разрядов.

Основные характеристики таких ходов приведены в [35, 36].

Полигонометрия строится в виде различных систем с узловыми точками или одиночными ходами для решения разнообразных задач при производстве изыскательских работ и разбивках сооружений.

В полигонометрической сети следует предусмотреть минимальное число порядков, ограничиваясь, как правило, полигонометрией 4 класса и 1 разряда.

Исходными данными для полигонометрических сетей служат пункты построений более высокого класса. В зависимости от выбора исходных данных сеть может рассматриваться как свободная или несвободная.

Более подробно вопросы построения инженерно-геодезических сетей методом полигонометрии, оценки проектов, нолевых измерений и прочее рассмотрены отдельно в главе 4.

Таблица 2.4. Некоторые характеристики построения опорных сетей способом

Предельные длины отдельного хода при измерении линий электронными тахеометрами, км (п — число сторон)

8 при т?=30 12 при н=15 20 при л=6

10 при п=50 15 при п=25 25 при п=10

6 при и=30
10.. ..н=10
14.. ..я=6

Предельные длины сторон

Средняя квадратическая ошибка измерения угла по невязкам в ходах, с, не более

Угловая невязка в ходах или полигонах, с, не более

Предельная относительная погрешность хода

Количество приёмов измерения угла теодолитом ЗТ2КП

Периметр полигона, образованного ходами в свободной сети, км

Примечание к таблице 2.4: В ходах полигонометрии 1 разряда длиной до 1 км и 2 разряда длиной до 0,5 км допускается абсолютная линейная невязка 10 см.

Линейно-угловые сети. Линейно-угловые сети определяются как построенные на местности примыкающие друг к другу геометрические фигуры из треугольников, четырёхугольников и центральных систем, в которых измерены все стороны и все углы, или часть углов и все стороны, или ряд сторон и все углы. Естественно, вершины фигур закрепляются на местности подземными центрами и обозначаются наружными знаками.

При построении инженерно-геодезических разбивочных сетей существенными являются не только высокие требования к точности планового положения пунктов, но и к равномерному распределению ошибок по сети. В этом свете описанные ранее способы построения разбивочных сетей имеют некоторые специфические недостатки. Так, главным недостатком триангуляции является резкое падение точности определения длин сторон при увеличении расстояния между базисом и определяемой стороной, особенно при резко неравносторонней форме треугольников, что часто встречается в инженерно-геодезических сетях. Основной недостаток трилатерации состоит в том, что если форма треугольников значительно отличается от равносторонней, то углы, вычисленные но измеренным сторонам, имеют существенную неравноточность.

Линейно-угловые сети лишены этих недостатков и являются наиболее точными геодезическими построениями на местности, вбирающими в себя достоинства как триангуляции, так и трилатерации. Линейно-угловая сеть в 1,3 — 1,5 раза точнее триангуляции и трилатерации. В такой сети точность её элементов практически не зависит от формы треугольников, существенно уменьшается зависимость между продольным и поперечным сдвигами, обеспечивается весьма жёсткий контроль угловых и линейных измерений.

Вид и конфигурация инженерно-геодезических плановых сетей зависят от формы и размеров территории города или посёлка, строительной площадки или объекта строительства.

Для линейно-угловой сети геометрические параметры, схема построения, требования к точности измерения углов аналогичны сети триангуляции 4 класса. Требования к точности измерения длин сторон могут быть приняты, как в трилатерации. Так же, как и для трилатерации, оценка проекта линейно-угловой сети может быть выполнена двояко: на компьютере с применением существующих программ но обработке инженерно-геодезических измерений или по приближенным формулам.

Оценку точности линейно-угловых сетей выполняют в зависимости от её конструкции одним из двух методов.

1. Сеть построена так, что интересующий элемент может быть оценен раздельно по данным угловых и линейных измерений. Очевидно, для этого имеются исходные данные — координаты, дирекционные углы, базисные стороны и прочее. В рассматриваемом случае расчёт точности линейно-угловой сети значительно упрощается из-за того, что вес линейно-углового элемента равен сумме весов этого элемента из угловой и линейной сети, т. е.

следовательно,

2. Интересующие элементы сети могут быть оценены на основе совместных угловых и линейных измерений. В этом случае оценку точности линейноугловой сети выполняют по общим формулам средней квадратической ошибки функции уравненных величин.

Одним из существенных моментов оценки точности линейно-угловой сети является правильное соотношение ошибок угловых и линейных измерений. Оптимальное соотношение ошибок угловых и линейных измерений должно обеспечить равенство по модулю поперечного и продольного сдвигов конца любой стороны геодезической сети, т. е. |/я„| = т,. Это будет наблюдаться тогда, когда

Это равенство может быть нарушено в пределах до 3 раз в ту или другую сторону Здесь р — число секунд в радиане.

При необходимости введения весов измерений принимают:

От правильного соотношения Шр/т, зависит достоверность оценки проекта сети.

Для оценки проектируемой линейно-угловой сети, состоящей из равносторонних треугольников можно, использовать формулу средней квадратической ошибки связующей стороны после уравнивания. При прежних обозначениях для случая, когда измерены все стороны и все углы, имеем [17]:

Эта формула справедлива и для случая, когда измерены все углы и только связующие стороны.

Средняя квадратическая ошибка угла в равностороннем треугольнике после уравнивания, когда в сети измерены все углы и все стороны, может быть подсчитана по формуле: