Таблица радиусов вписанной и описанной окружностей для правильных многоугольников

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

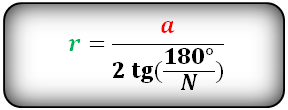
r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Видео:Геометрия для чайников 59 Формулы для радиусов вписанной и описанной окружностей правильных многоугоСкачать

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правильные многоугольники формулы площади, радиуса вписанной и описанной окружности (Таблица)

В справочной таблице приведены формулы (выражения) для радиусов описанной и вписанной окружностей и для площади некото­рых правильных многоугольников: треугольник, квадрат, пятиугольник, шестиугольник, восьмиугольник и десятиугольник.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.

Таблица правильные многоугольники (длина стороны равна α)

Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Формулы радиусов вписанных и описанных окружностей правильных многоугольников

Просмотр содержимого документа
«МКОУ»

МКОУ «Волчихинская СШ №2»

Учитель Бакута Е.П.

Урок по теме «Формулы радиусов вписанных и описанных окружностей правильных многоугольников»

Образовательные: изучение формул радиусов вписанных и описанных окружностей правильных многоугольников;

Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.

Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.

Оборудование: Мультимедийный компьютер, мультимедиапроектор, экспозиционный экран

1. Организационный момент

Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

В математики мир отправимся смело,

В мир примеров и разных задач.

А девизом нашего урока буду такие слова:

И открытия нас ждут обязательно!

Сегодня на уроке мы узнаем и увидим много нового и интересного: вспомним понятие правильного многоугольника, выведем формулы, связывающие площадь и сторону правильного многоугольника с радиуса вписанной окружности. Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой…”.

3. Актуализация опорных знаний. Проверка д/з.

Какая фигура называется многоугольником?

Какой многоугольник называется правильным?

Какое другое название правильного треугольника?

Какое другое название правильного четырехугольника?

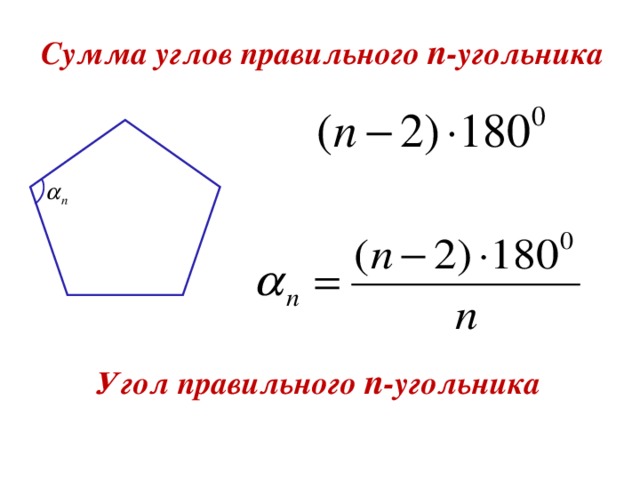
Формула суммы углов выпуклого многоугольника.

Формула угла правильного многоугольника.

4. Изучение нового материала. (слайды)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на окружности.

Окружность можно вписать или описать около любого треугольника, причём центр вписанной в треугольник окружности лежит на пересечении биссектрис треугольника, а центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров.

Около любого правильного многоугольника можно описать окружность, и в любой правильный многоугольник можно вписать окружность, причём центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника.

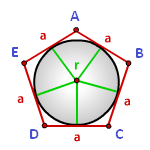
Радиус вписанной окружности в правильный многоугольник (r):

a — сторона многоугольника, N — количество сторон многоугольника

Радиус описанной окружности правильного многоугольника(R):

a — сторона многоугольника, N — количество сторон многоугольника.

Заполним таблицу для правильного треугольника, правильного четырехугольника, правильного шестиугольника.

5. Закрепление нового материала.

Решить № 1088, 1090, 1092, 1099.

6. Физминутка. Раз – потянуться Два – нагнуться

Три – оглянуться Четыре – присест

Пять – руки вверх Шесть – вперед

Семь – опустили Восемь – сели

Девять – встали Десять – снова сели

7. Самостоятельная работа учащихся (работа в группах)

8.Итоги урока. Рефлексия. Д/з.

— Какое впечатление у Вас сложилось? (Понравилось – не понравилось)

– Какое настроение после урока? (Радостное – грустное)

– Какое самочувствие? (Устал – не устал)

– Какое отношение к пройденному материалу? (Понял – не понял)

– Какова твоя самооценка после урока? (Доволен – не доволен)

– Оцени свою активность на уроке. (Старался – не старался).

Есть у математики молва,

Что она в порядок ум приводит,

Потому хорошие слова

Часто говорят о ней в народе.

Ты нам, геометрия, даёшь

Для победы важную закалку.

Учится с тобою молодёжь

Развивать и волю, и смекалку.

Примечание Презентация содержит разделы:

Повторение теоретического материала

Проверка домашнего задания

Вывод основных формул, т.е. новый материал

Закрепление: решение задач в группах и самостоятельно

Просмотр содержимого презентации
«9_klass_pravilnye_mnogougolniki_urok_2»

Формулы для вычисления площади правильного многоугольника, его стороны и радиусов описанной и вписанной окружности.

• Чтобы спорилось нужное дело,
• Чтобы в жизни не знать неудач,
• В математики мир отправимся смело,
• В мир примеров и разных задач.

И открытия нас ждут обязательно!

Сегодня на уроке мы узнаем и увидим много нового и интересного: вспомним понятие правильного многоугольника, выведем формулы, связывающие площадь и сторону правильного многоугольника с радиуса вписанной окружности. Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой…”.

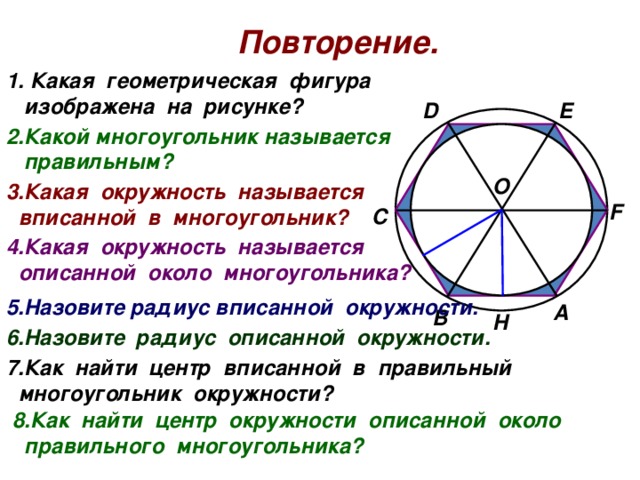
изображена на рисунке?

2.Какой многоугольник называется

3.Какая окружность называется

вписанной в многоугольник?

4.Какая окружность называется

описанной около многоугольника?

5.Назовите радиус вписанной окружности.

6.Назовите радиус описанной окружности.

7.Как найти центр вписанной в правильный

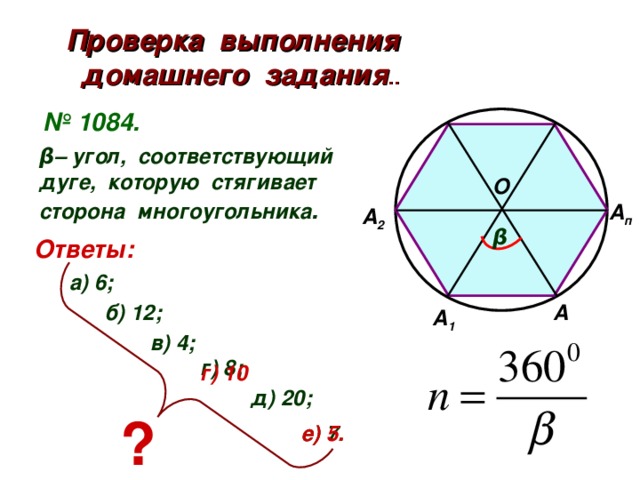
8.Как найти центр окружности описанной около

дуге, которую стягивает

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

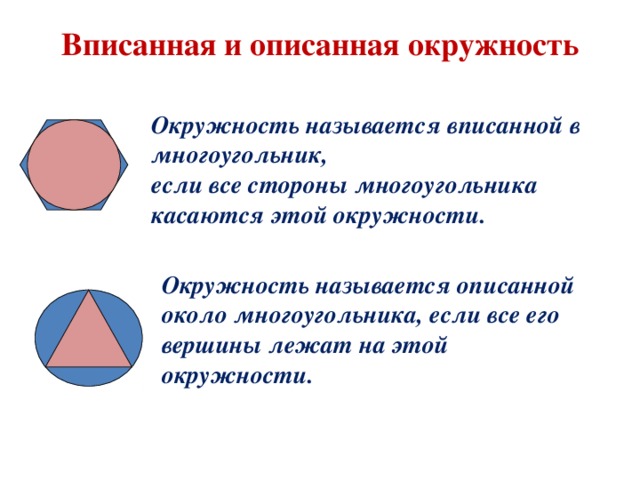
Вписанная и описанная окружность

Окружность называется вписанной в многоугольник,

если все стороны многоугольника касаются этой окружности.

Окружность называется описанной около многоугольника, если все его вершины лежат на этой

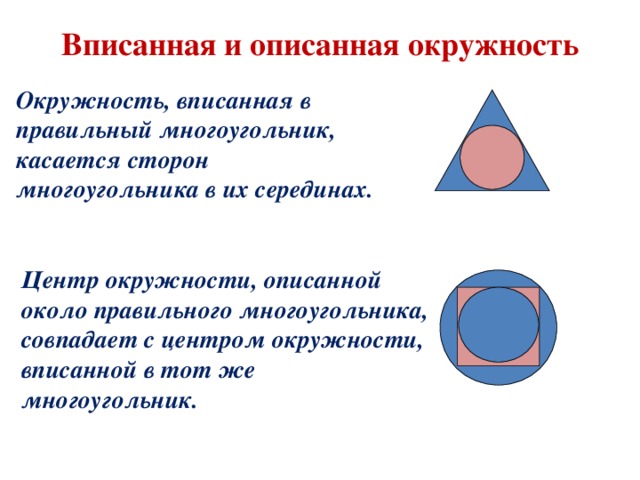
Вписанная и описанная окружность

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Выведем формулу радиуса вписанной и радиуса описанной окружности правильного многоугольника.

Пусть r – радиус вписанной окружности,

R – радиус описанной окружности,

п – количество сторон и углов многоугольника.

Рассмотрим правильный п-угольник.

Пусть а – сторона п-угольника,

Построим точку О – центр вписанной и описанной окружности.

∟ С = 90 º — (по построению),

∟ ОАС = α /2 — (ОА – биссектриса угла п- угольника),

АС = а/2 – (ОС – медиана к основанию равнобедренного треугольника),

🎬 Видео

Формулы для радиусов вписанной и описанной окружностей треугольника Геометрия 9классСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Формулы радиуса описанной и вписанной окружности правильного многоугольника /9 класс/ СШ №1Скачать