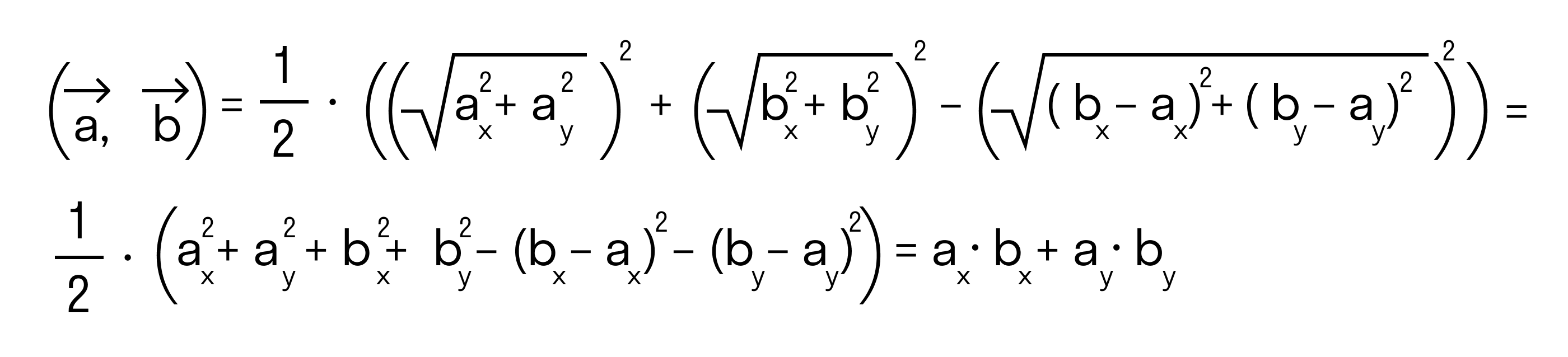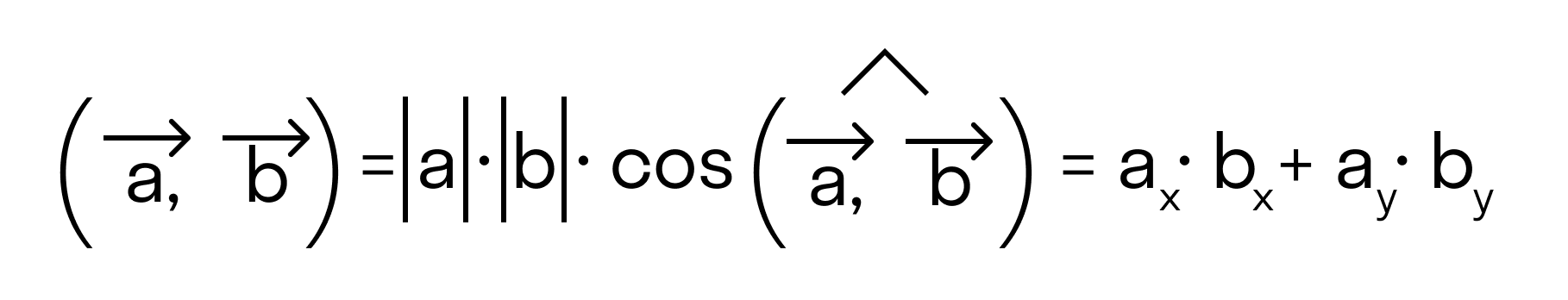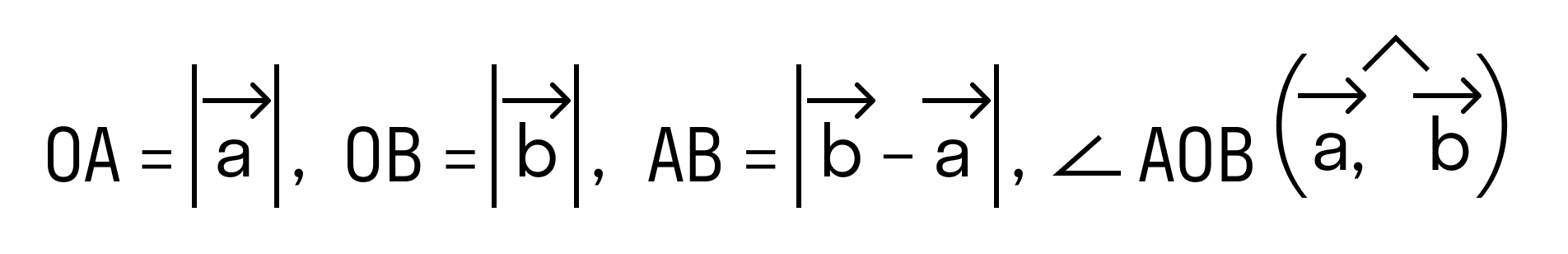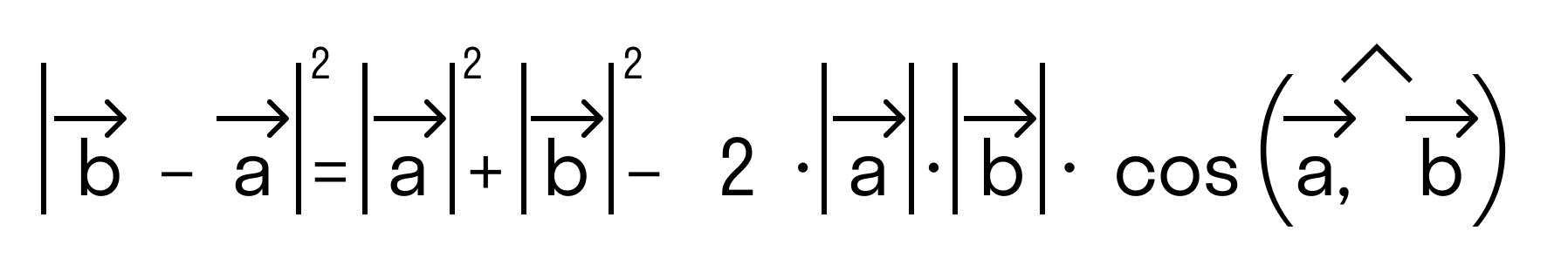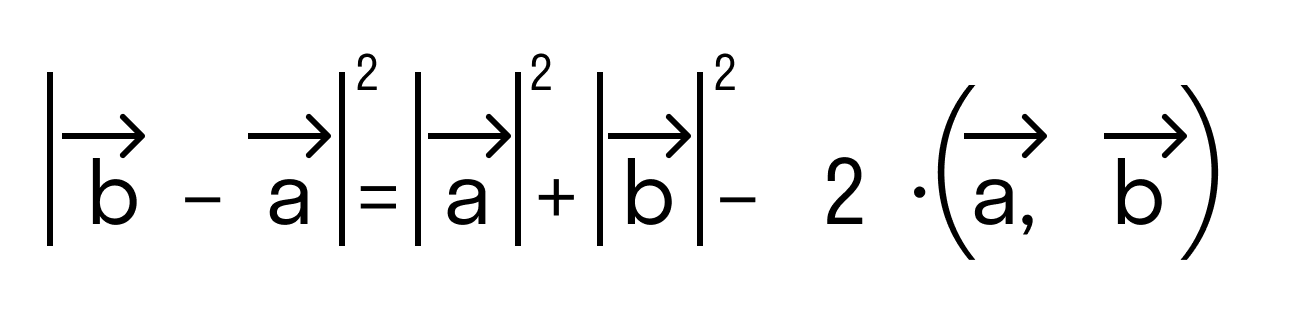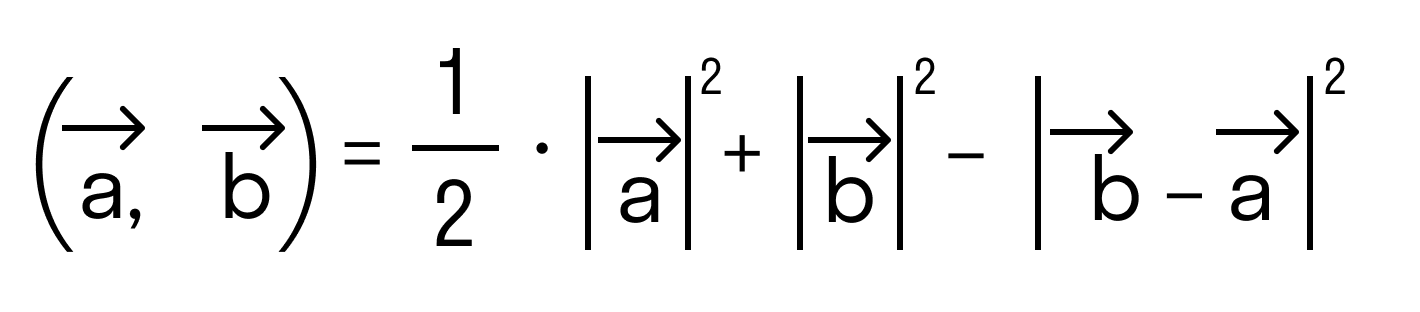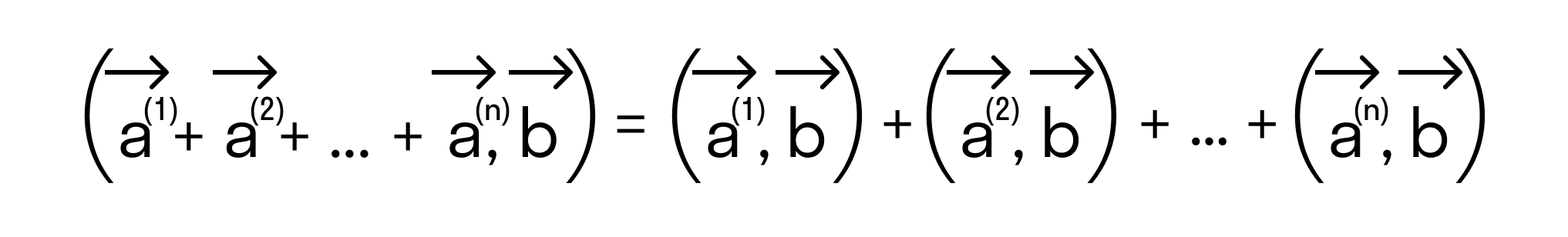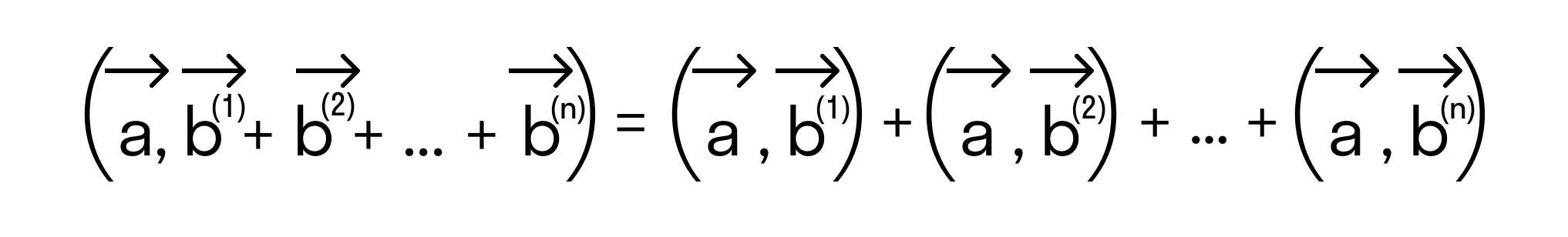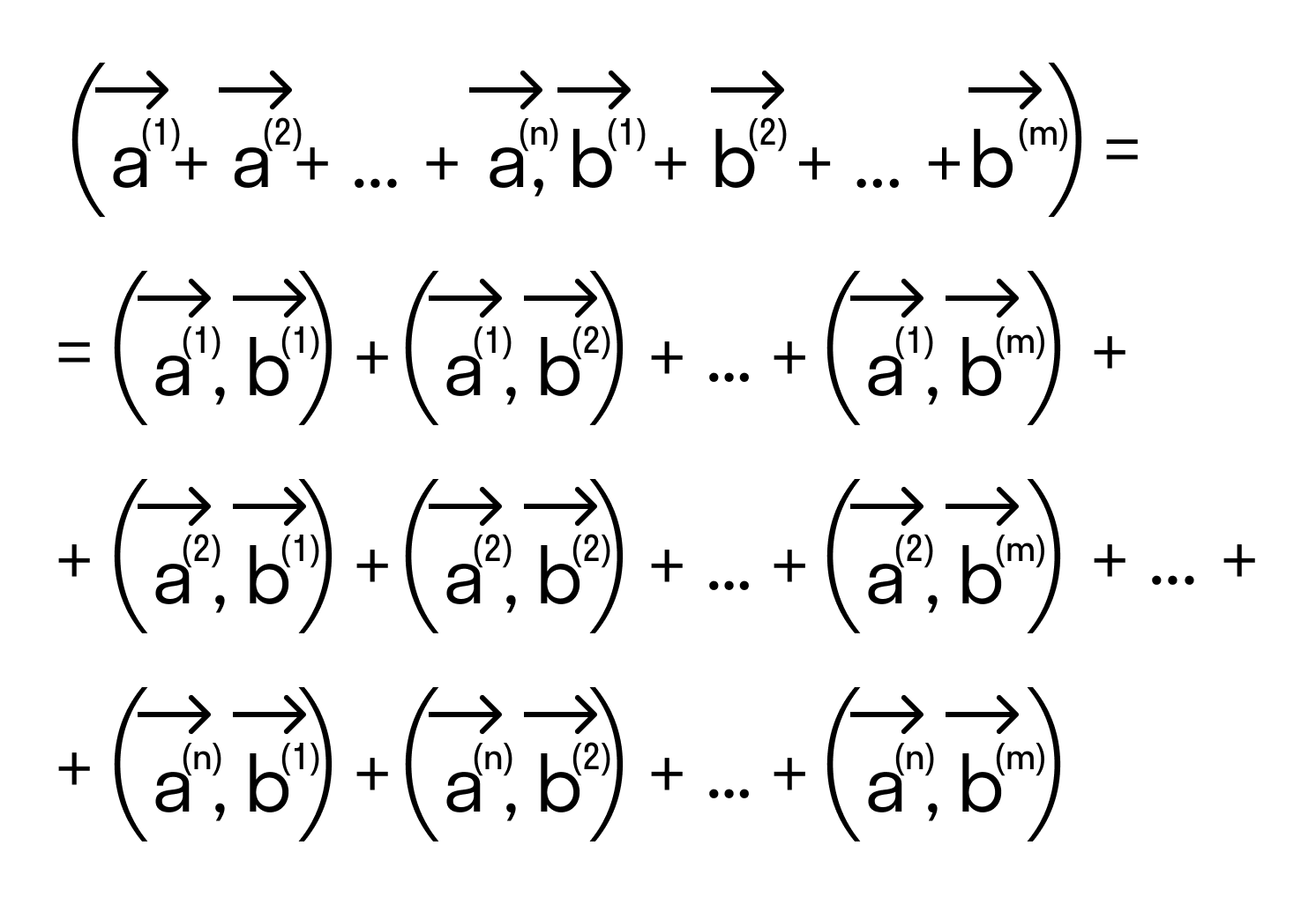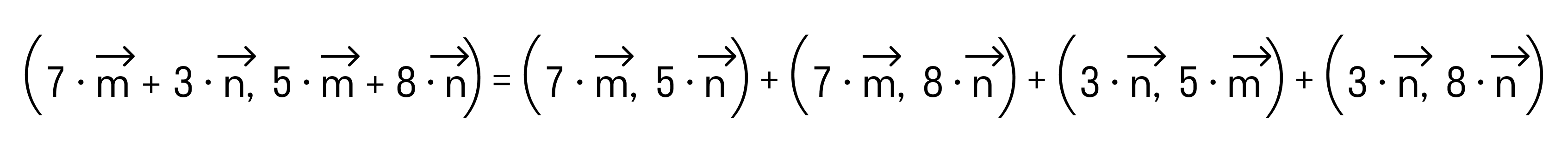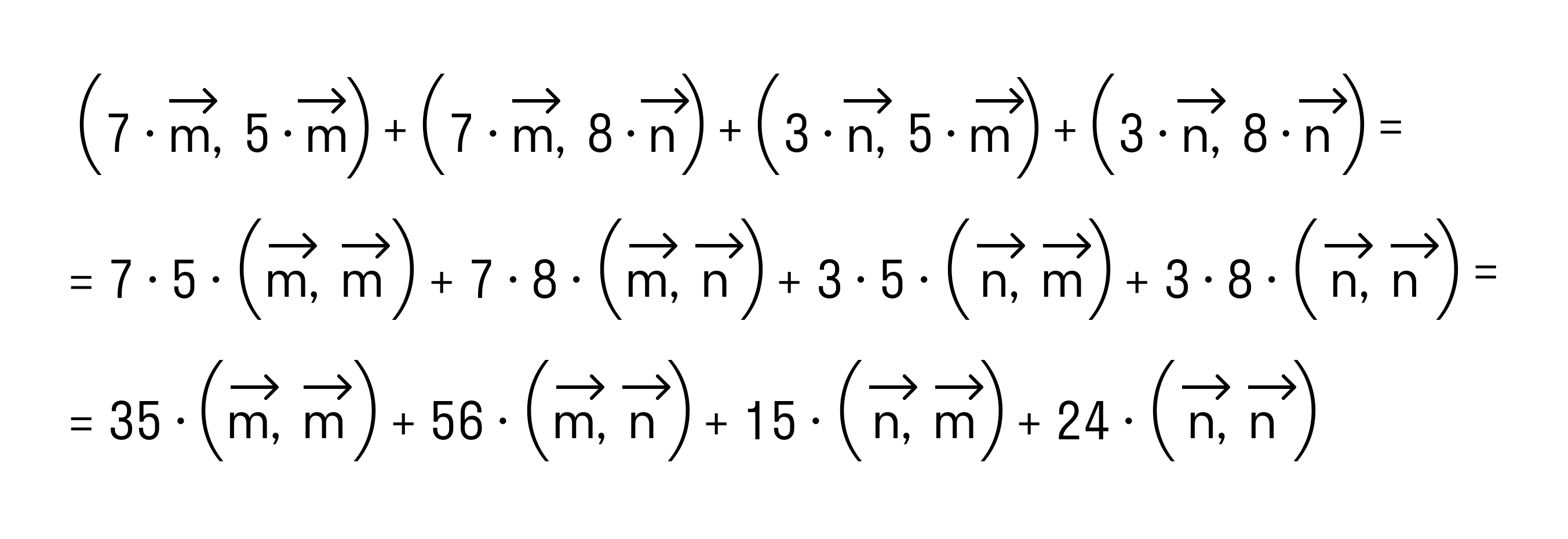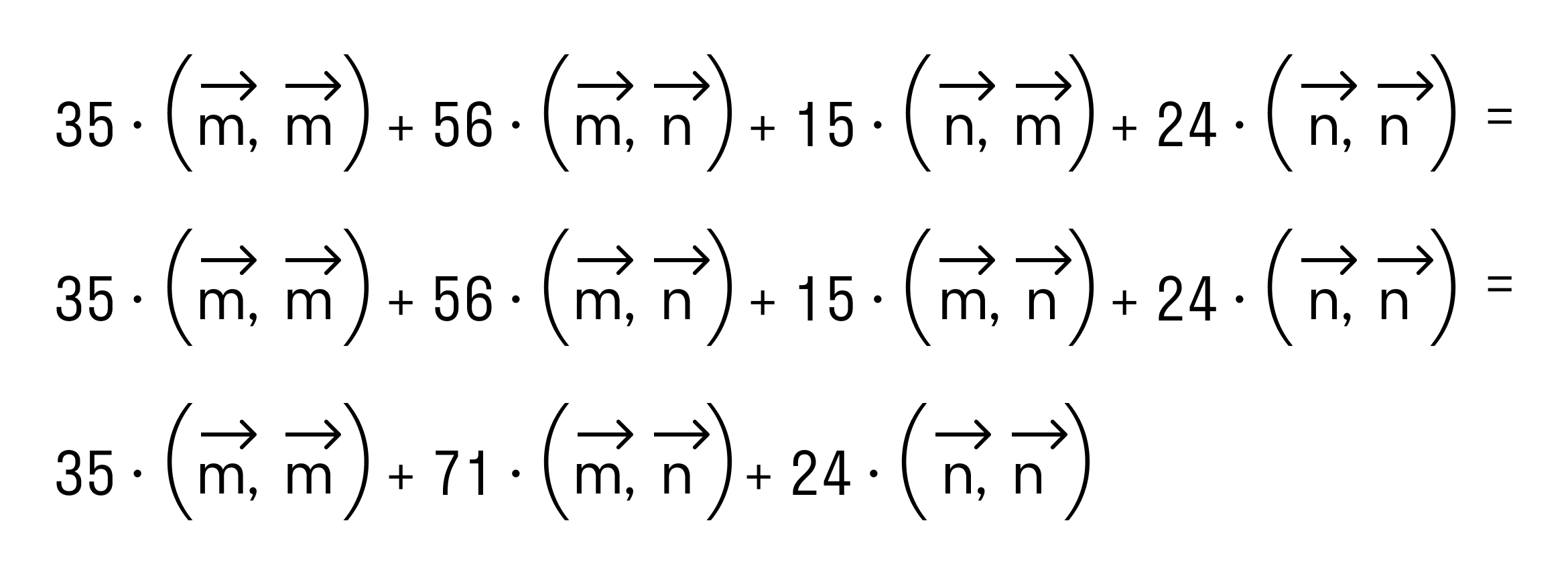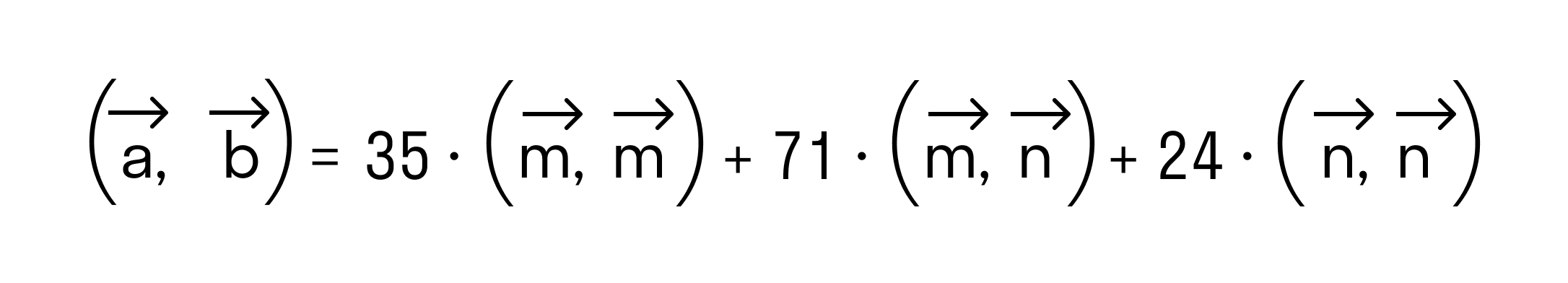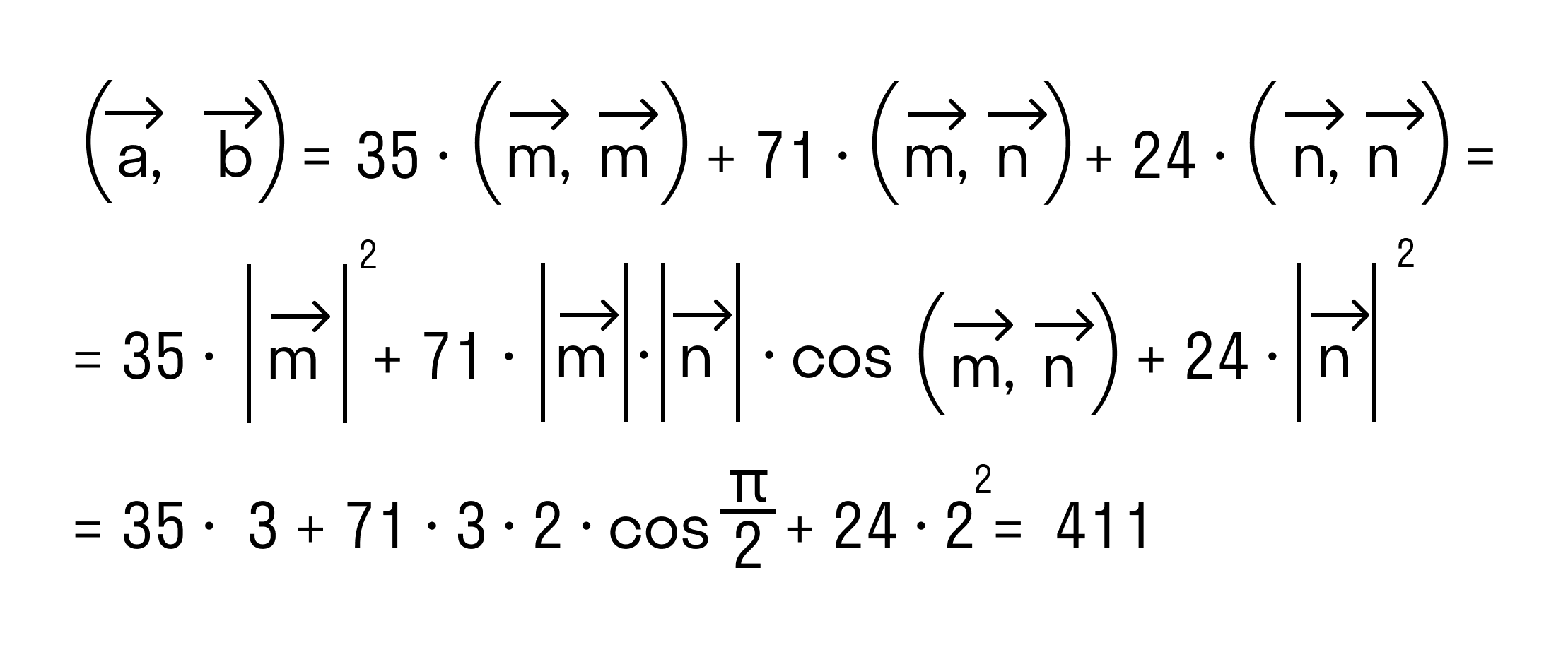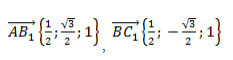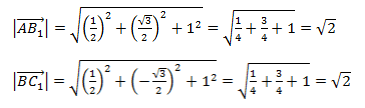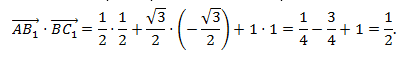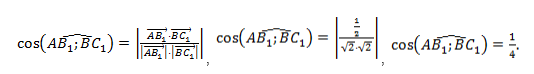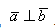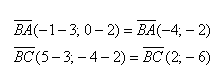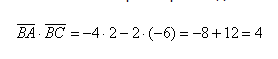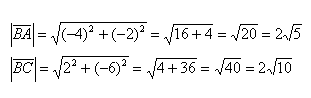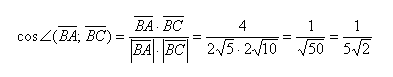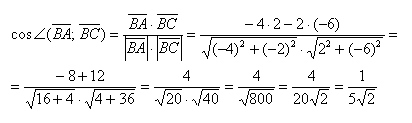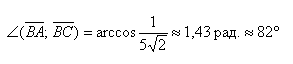Геометрия | 5 — 9 классы
В треугольнике ABC дано : АС(вектор) = (вектор) а, АB(вектор) = (вектор)b, AD — медиана.
Найдите вектор 1 / 4 AD(вектор).
Если построить параллелограмм на векторах АВ и АС, то АД половина диагонали и вектор АД = 1 / 2(а + в), 1 / 4АД = 1 / 8(а + в).
- В треугольнике ABC AC = a, AB = b, AD — медиана?
- Отрезок BB1 — медиана треугольника ABC?
- Дано : вектор a(2 ; 3), вектор b(9 ; — 9), вектор с = вектор а — 1 / 3 * векторb, надо найти координаты вектора c и его длину?
- Отрезок BB1 — медиана треугольника ABC?
- В треугольнике ABC AM медиана вектор AB = вектор a вектор AC = вектор b выразите векторы AM CB MC через векторы a и b?
- В треугольнику АВС о — точка пересечения медиан?
- В треугольнике ABC o — точка пересечения медиан?
- Отрезок bk — медиана треугольника abc?
- Точка О середина медианы AD треугольника ABC?
- В треугольнике ABC O — точка пересечения медиан?
- В треугольнике abc даны векторы
- Скалярное произведение векторов
- Основные определения
- Угол между векторами
- Скалярное произведение векторов
- Скалярное произведение в координатах
- Формулы скалярного произведения векторов заданных координатами
- Свойства скалярного произведения
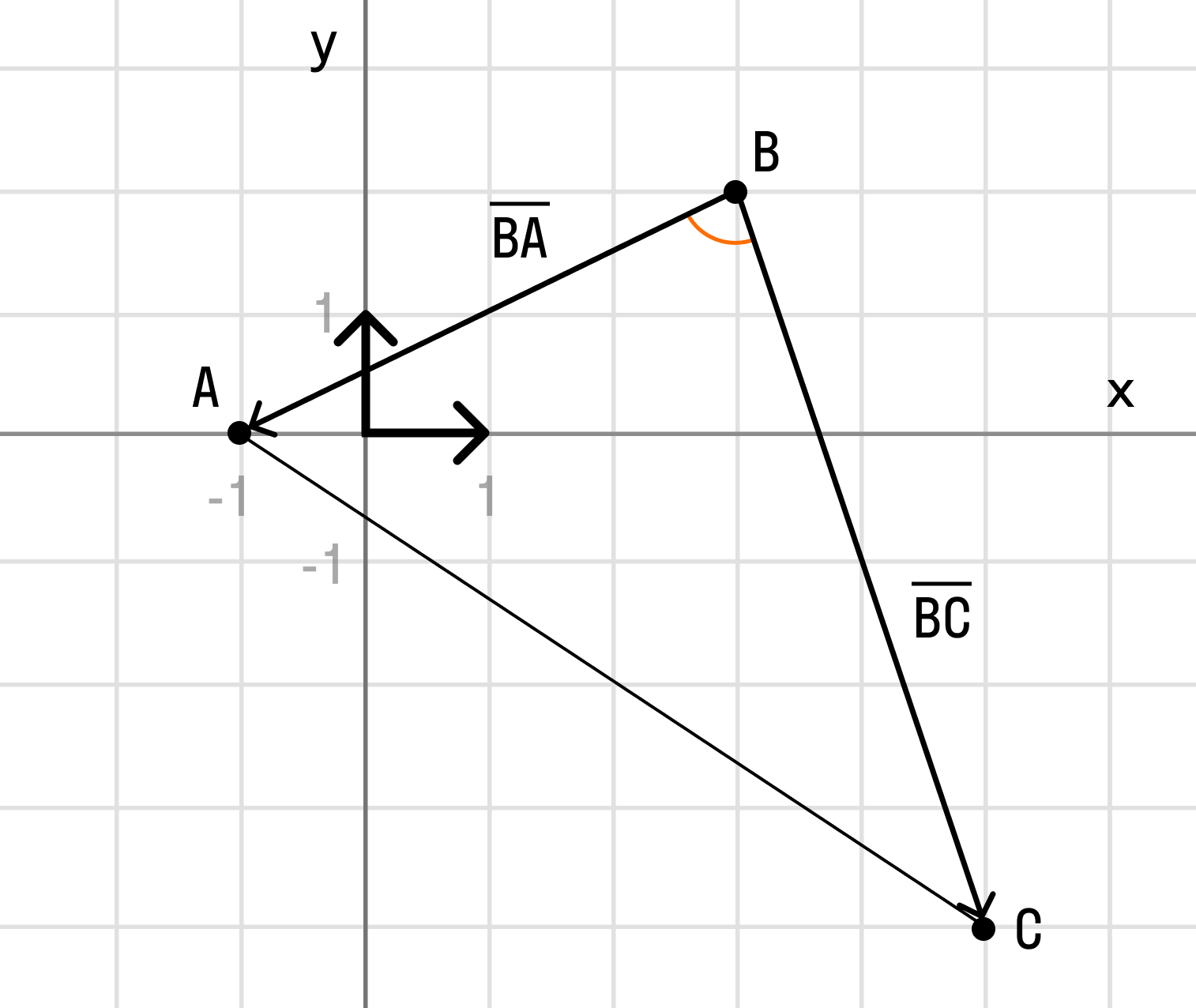
- Примеры вычислений скалярного произведения
- В треугольнике АВС укажите векторы : а) АВ + ВС б)СВ + ВА в)СА + АВ г)ВА + СВ д)ВА + СА?
- Дан треугольник АВС, Выразите вектор СВ через векторы АС и АВ?
- Дан треугольник АВС Вектор АВ = с вектор ВС = а вектор СА = в?
- В треугольнике АВС, известно, что АВ = ВС < ; АВС = 128 градусов найдите < ; ВСА?
- В треугольнике АВС АС равна 9, ВС равна 8, а угол ВСА равен 30 градусам?
- В равнобедренном треугольнике авс сторона ас — основание угол вса = 40 градусов угол авс = 100 градусов вд — медиана найдите углы треугольника авд?
- В треугольнику АВС о — точка пересечения медиан?
- В треугольнике АВС угол В = 48(град), а внешний угол при вершине А = 100(град) Найдите угол ВСА?
- В треугольнике авс ав равен вс угол абс равен 104 градуса найдите угол вса?
- В треугольнике АВС известно, что АВ = ВС, угол АВС = 144 грудуса?
- В равнобедренном треугольнике АВС сторона АС — основание, угол ВСА = 40, угол АВС = 100, ВD — медиана?
- В треугольнике АВС известно, что АВ = ВС, (угол)АВС = 106?
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

В треугольнике ABC AC = a, AB = b, AD — медиана?
В треугольнике ABC AC = a, AB = b, AD — медиана.
Найдите вектор 1 / 4 AD.
Видео:№763. В треугольнике АВС АВ=6, ВС=8, ∠B=90°. Найдите: а) |ВА|-|ВС| и |ВА- ВС|;Скачать

Отрезок BB1 — медиана треугольника ABC?
Отрезок BB1 — медиана треугольника ABC.
Выразите векторы B1C.
BC через X(вектор сверху) = AB1(вектор сверху) и y(вектор) = AB(вектор) с чертежом.
Видео:№767. Дан треугольник ABC. Выразите через векторы а=АВ и b=АС следующие векторы:Скачать

Дано : вектор a(2 ; 3), вектор b(9 ; — 9), вектор с = вектор а — 1 / 3 * векторb, надо найти координаты вектора c и его длину?
Дано : вектор a(2 ; 3), вектор b(9 ; — 9), вектор с = вектор а — 1 / 3 * векторb, надо найти координаты вектора c и его длину.
Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

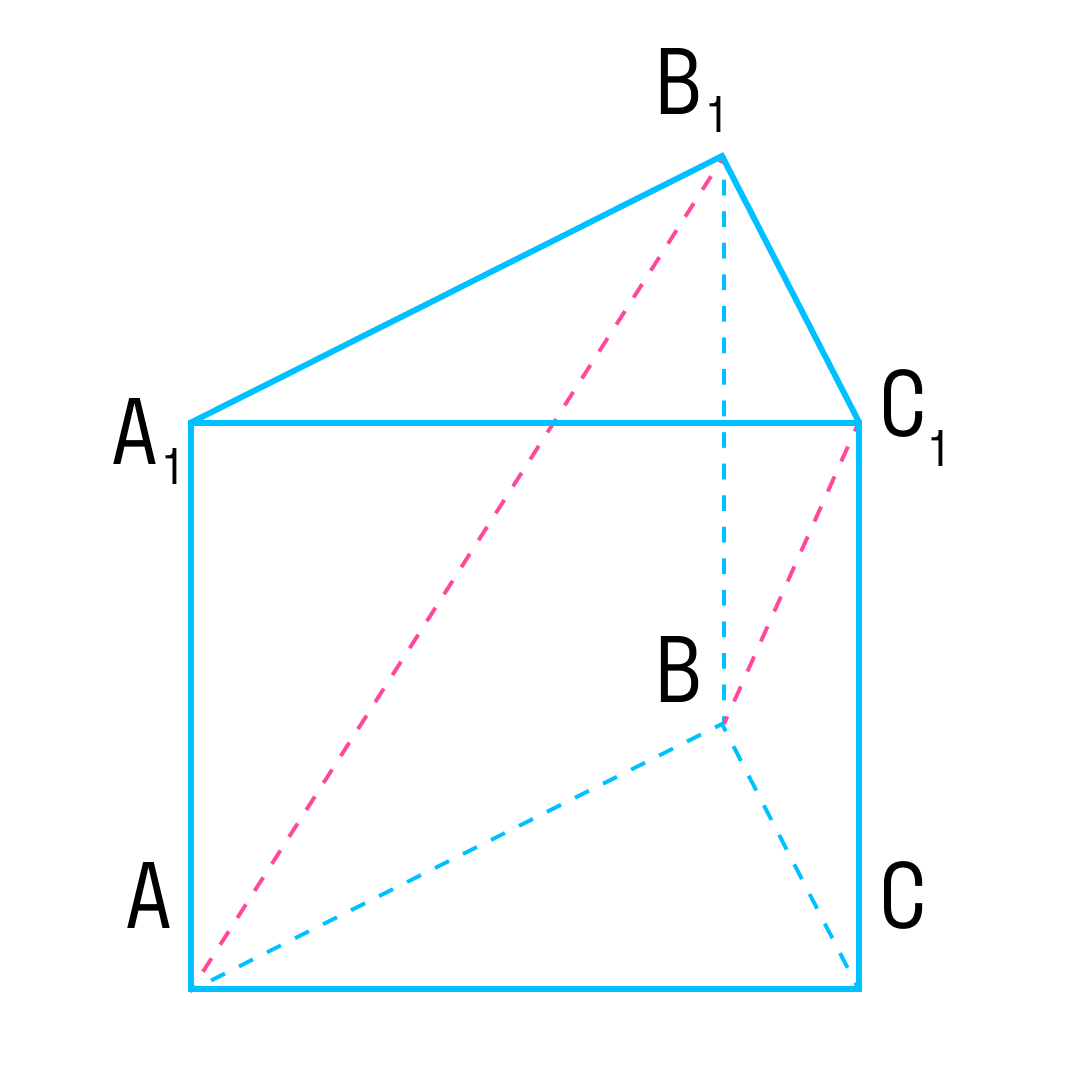
Отрезок BB1 — медиана треугольника ABC?
Отрезок BB1 — медиана треугольника ABC.
Выразите векторы B1C.
BC через x = вектору AB1 и y = AB.
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

В треугольнике ABC AM медиана вектор AB = вектор a вектор AC = вектор b выразите векторы AM CB MC через векторы a и b?
В треугольнике ABC AM медиана вектор AB = вектор a вектор AC = вектор b выразите векторы AM CB MC через векторы a и b.
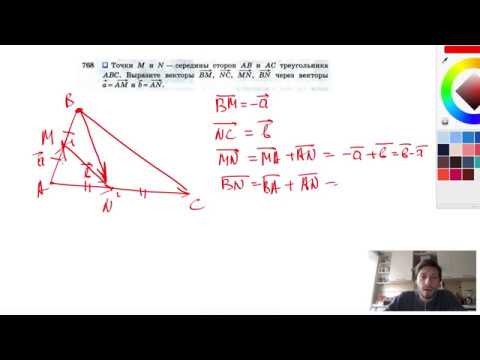
Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать
В треугольнику АВС о — точка пересечения медиан?
В треугольнику АВС о — точка пересечения медиан.
Вырази вектор ОА через вектор а = вектору АВ, вектор в = вектору АС.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

В треугольнике ABC o — точка пересечения медиан?
В треугольнике ABC o — точка пересечения медиан.
Выразите вектор AO через векторы a = AB и b = AC.
Видео:Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Отрезок bk — медиана треугольника abc?
Отрезок bk — медиана треугольника abc.
Найдите сумму векторов ak и bk.
Видео:Скалярное произведение векторов. 9 класс.Скачать

Точка О середина медианы AD треугольника ABC?
Точка О середина медианы AD треугольника ABC.
Выразите вектор AO через векторы а = BA и b = BC.
Видео:Угол между векторами. 9 класс.Скачать

В треугольнике ABC O — точка пересечения медиан?
В треугольнике ABC O — точка пересечения медиан.
Выразите вектор AO через векторы a = AB и b = AC с рисунком, спасибо.
На этой странице находится вопрос В треугольнике ABC дано : АС(вектор) = (вектор) а, АB(вектор) = (вектор)b, AD — медиана?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
180º(развернутый угол) — 130º(угол при вершине) = 50º ; далее из 180º(сумма углов в треугольнике) — 50º = 130 — сумма углов при основании, т. К треугольник равнобедренный, то углы при основании равны. Следовательно меньший угол можно получить путем..
1)ОС = ОВ Кут ВСО = Куту СВО = 35 градусів кут ОВА = 90 градусів кут АВС = 90 — 35 = 55 градусів.
По св — ву прямоугольного треугольника 2АD(твоя высота) = АВ(гипотенуза) = 6см 6см * 4 = 24 см( периметр ромба) Пожалуйста)))))))).
Извеняюсь за качество фото. Я думаю решение должно выглядеть так.
Напиши что сделать мы сделаем в пределах разумного.
Что делать то хоть напиши.
Вначале докажем что эти 2 треугольники соответственно равны. Можно доказать это по первой теореме. Углы B и D равны — так как они прямые, BC и AD равны — по условию, AC общая сторона. 1. Из — за того что эти треугольники равны, то и стороны в них ..
S = Pl / 2 В основании равностороннийтреугольник 1) P = 2 * 3 = 6 ; r = 1 / √3 ; l = √(9² + 1 / 3) = 9. 01 ; S = 6 * 9 / 2 = 27≠36 см² 3) P = 3 * 3 = 9 ; r = 3 / 2√3 ; l = √(9² + 9 / 12) = 9. 04 ; S = 9 * 9 / 2 = 40≠36 см² →В основании не равностор..
Если треугольник равнобедренный иоснование = 3 м, то третья сторона = 4 м Если угол против катета = 30 град , то 3 * 2 = 6 м.
ΔАВD. АD² = АВ² — ВD² = 625 — 576 = 49 ; АD = √49 = 7 см. ΔВСD. СD² = ВС² — ВD² = 1600 — 576 = 1024 ; СD = √1024 = 32 см. АС = АD + СD = 7 + 32 = 39. S(АВС) = 0, 5·24·39 = 12·39 = 468 см².
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

В треугольнике abc даны векторы
Видео:№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

Скалярное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Вычитание векторов. 9 класс.Скачать

Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
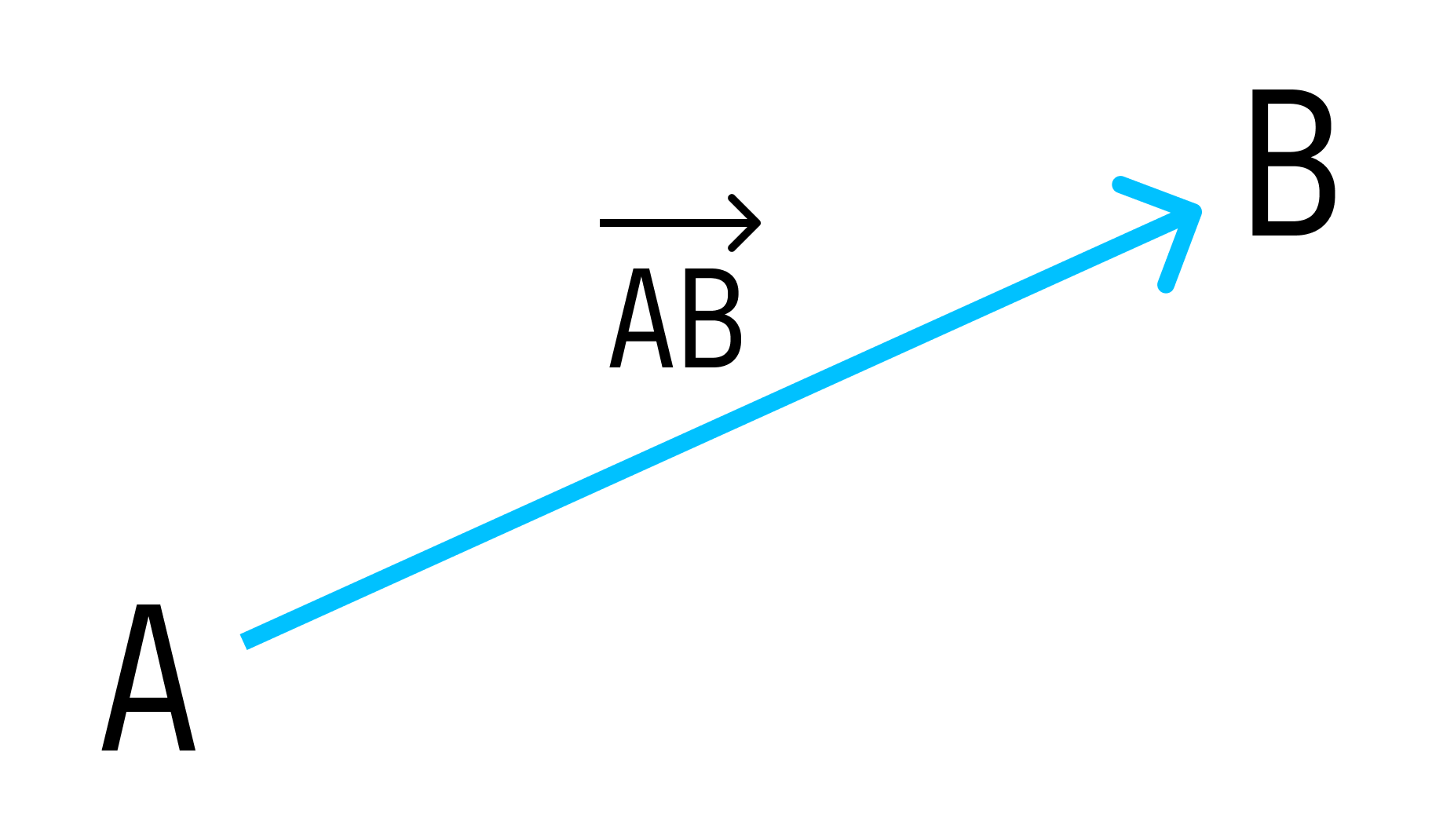
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Угол между векторами
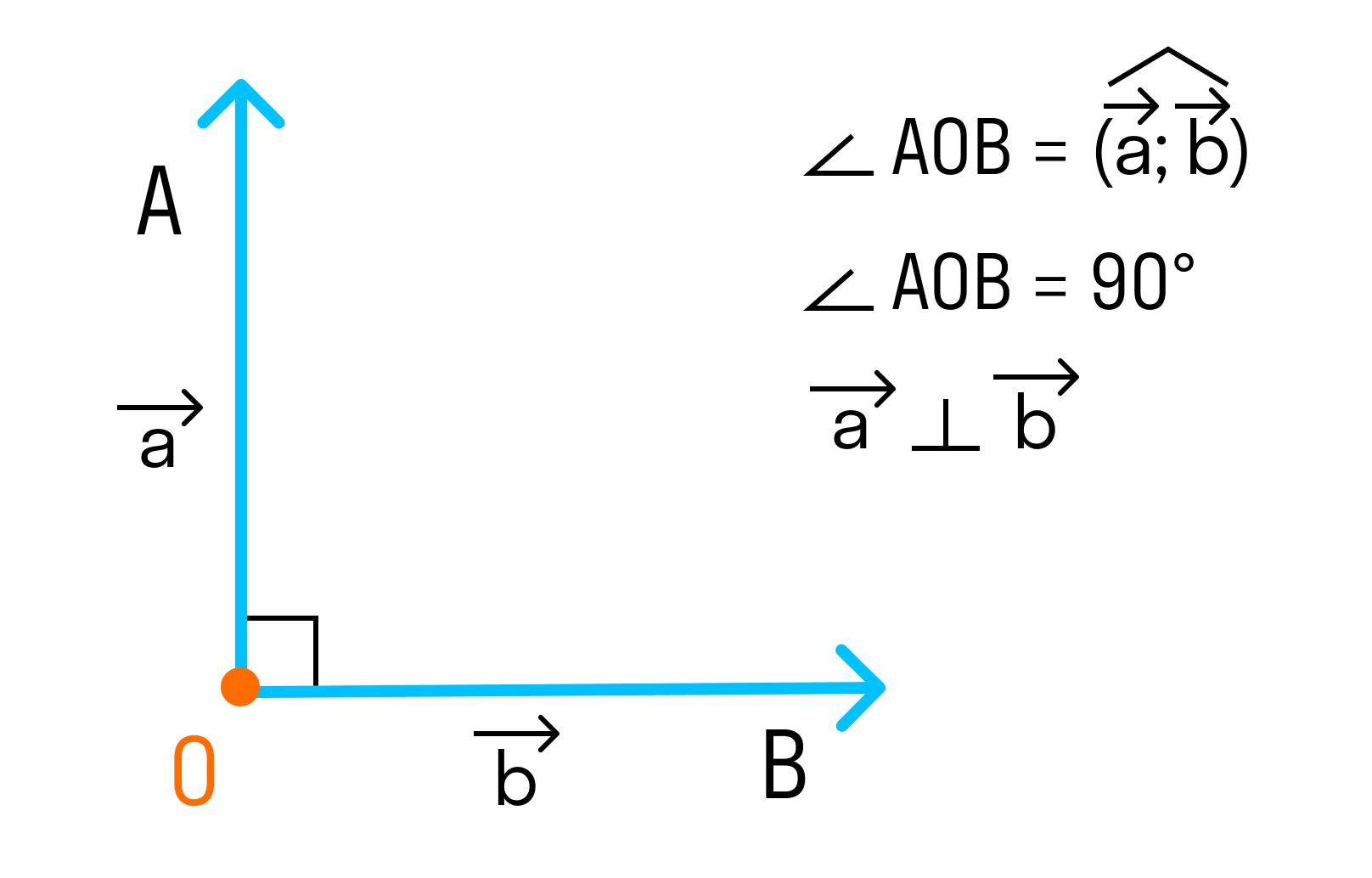
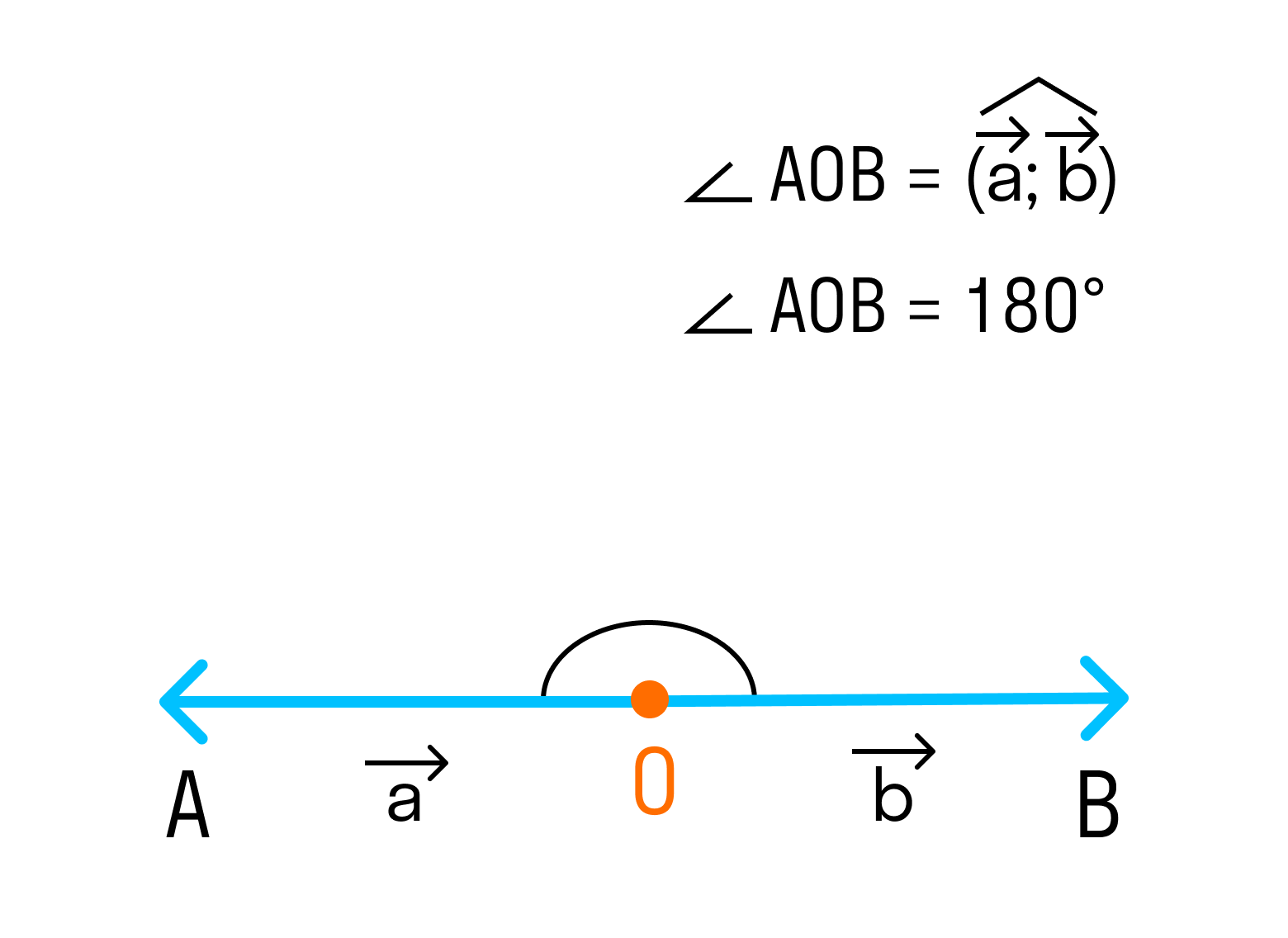
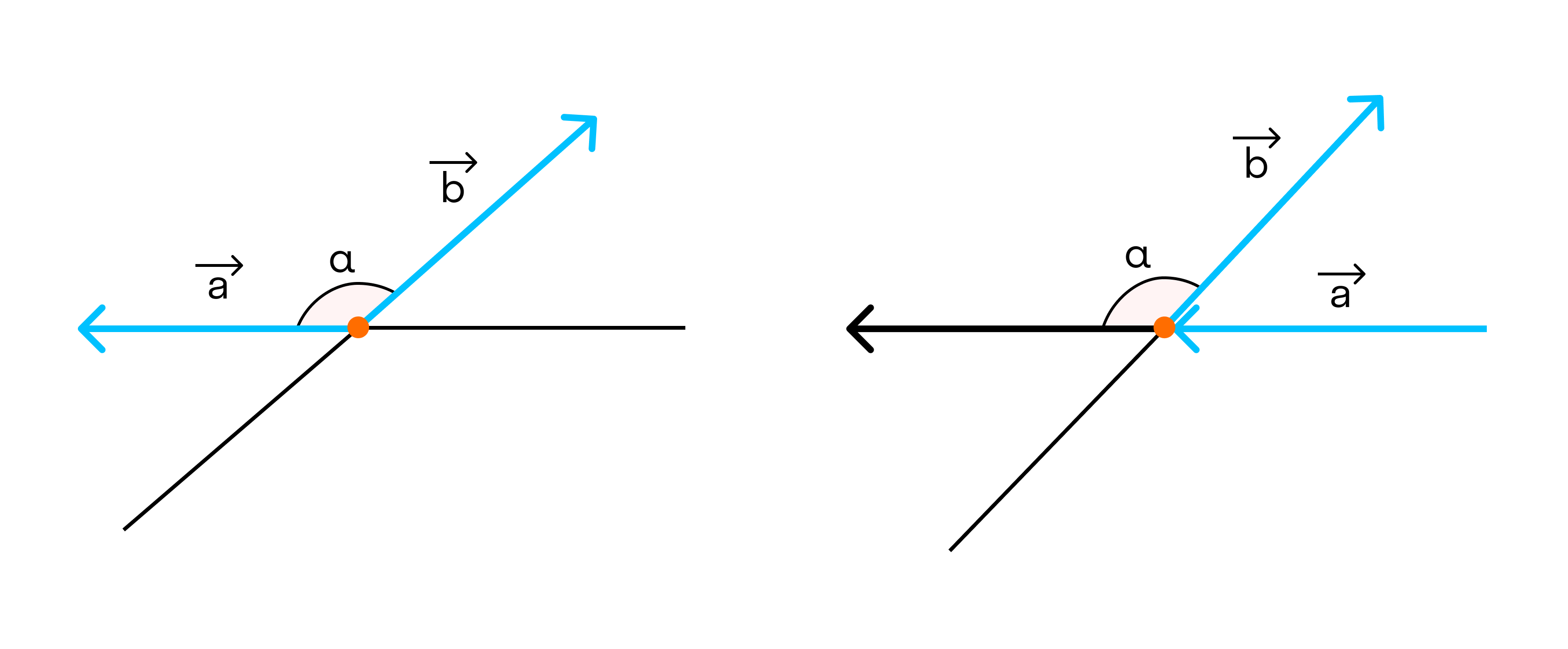
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Также векторы могут образовывать тупой угол. Это выглядит так:
Видео:Координаты вектора. 9 класс.Скачать

Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
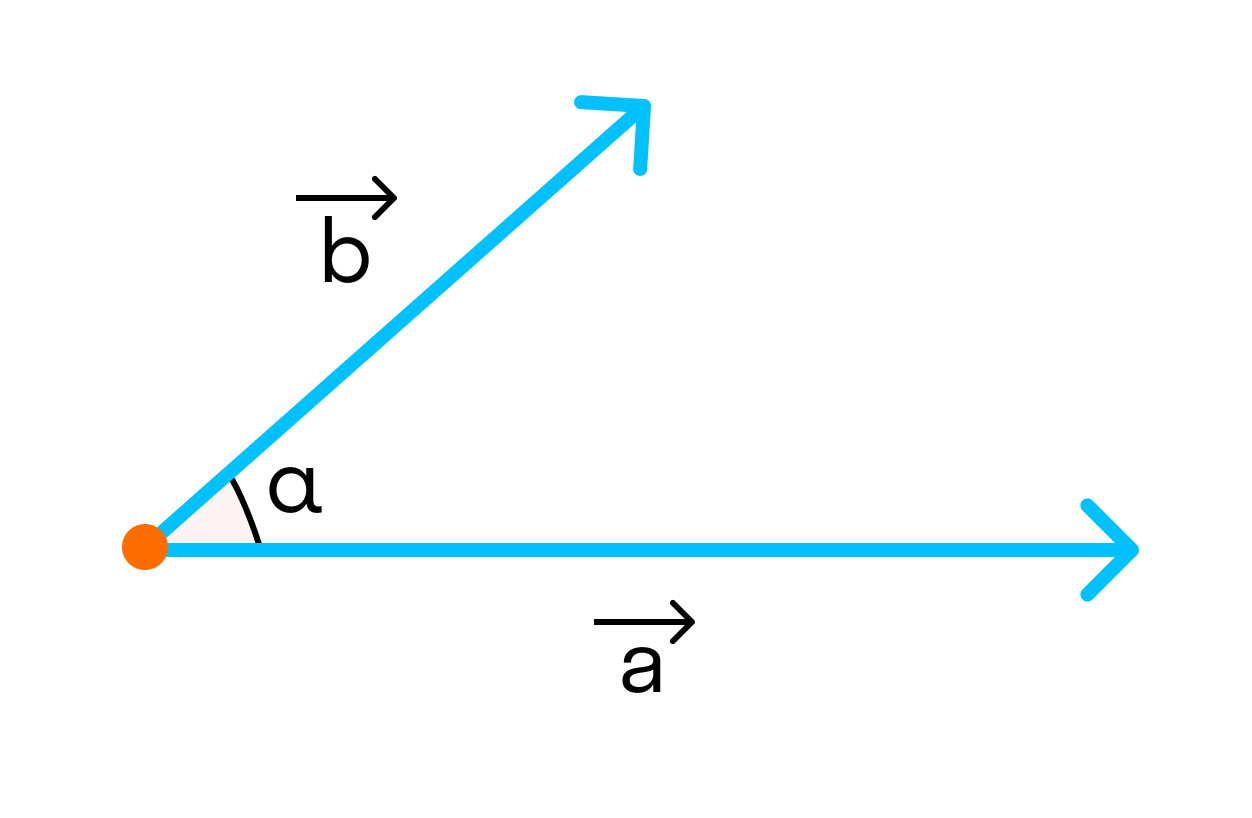
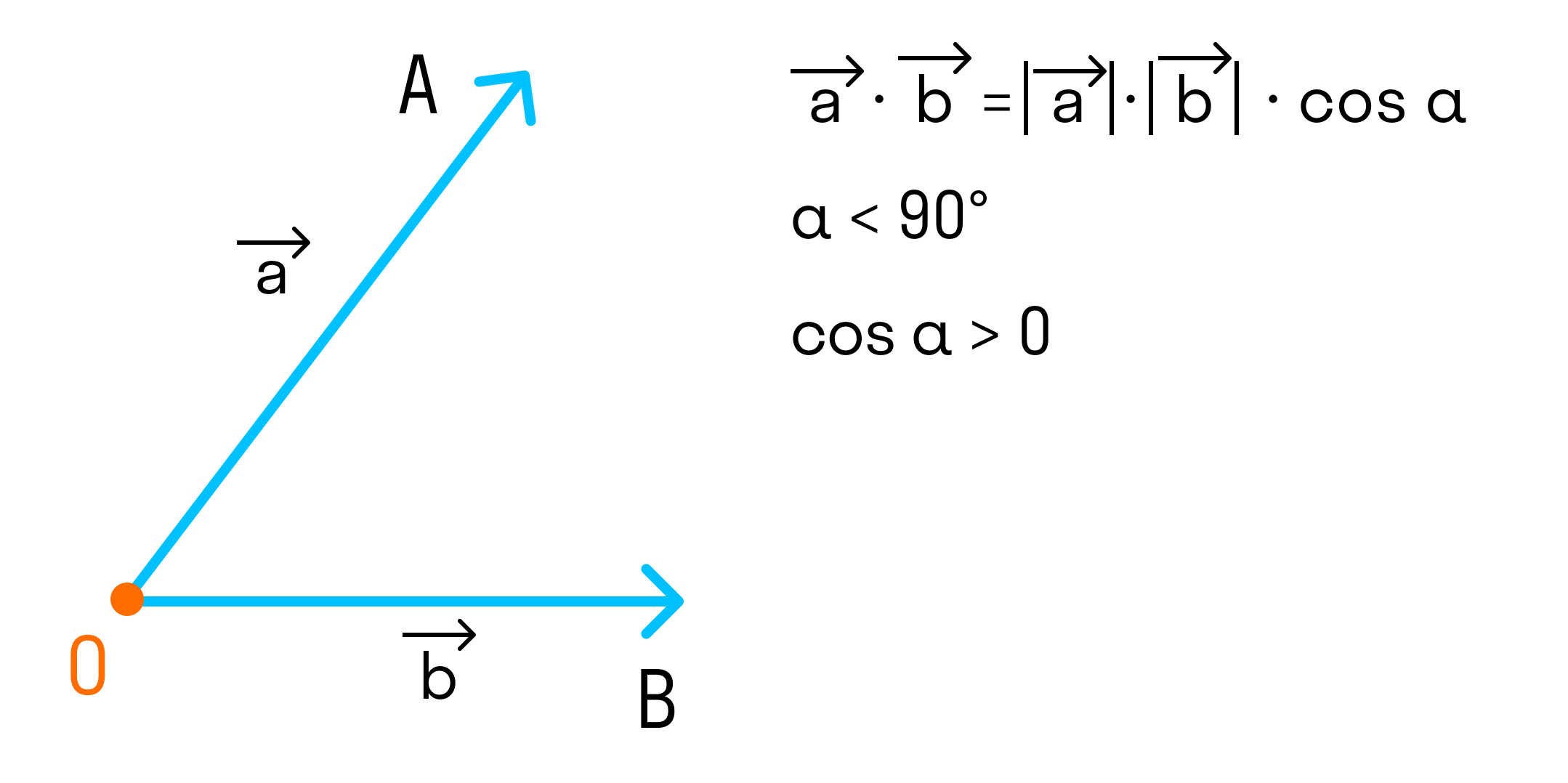
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα
Видео:№336. Даны точки A, В, С и D. Представьте вектор АВ в виде алгебраической суммы следующихСкачать

Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем