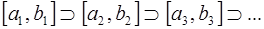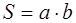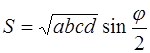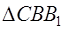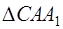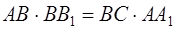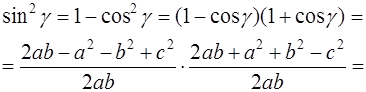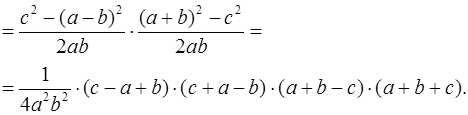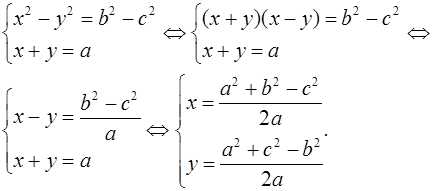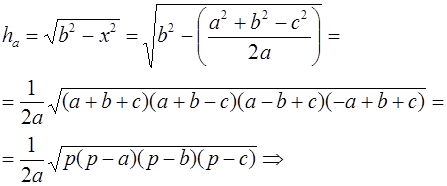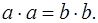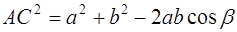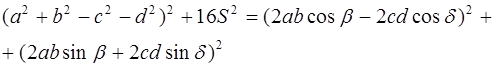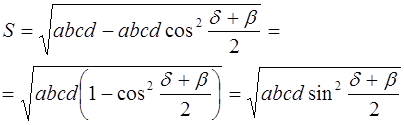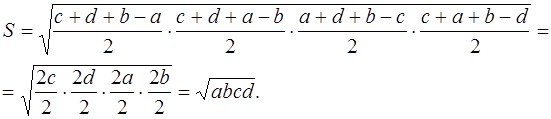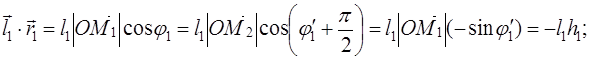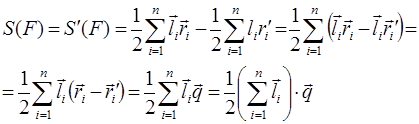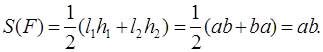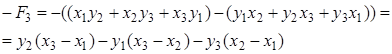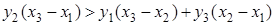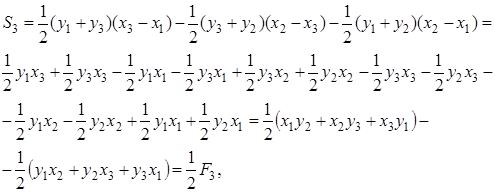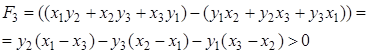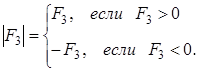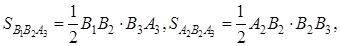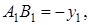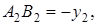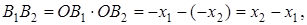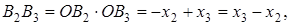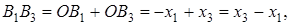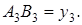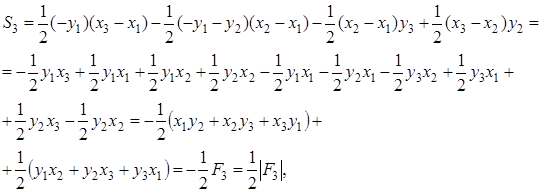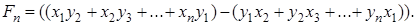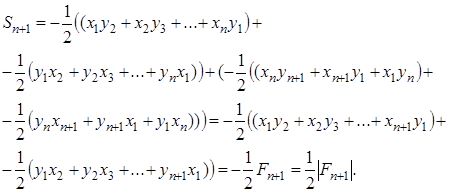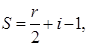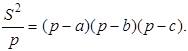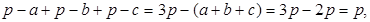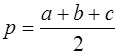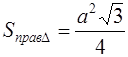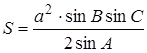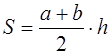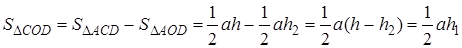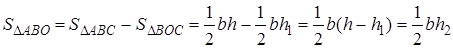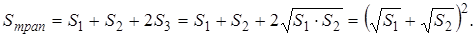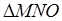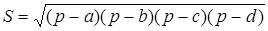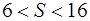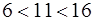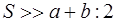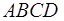Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
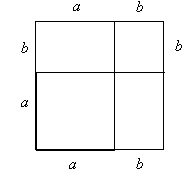
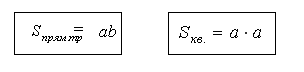
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- Информация к проектно-исследовательской работе по теме: «Формулы площадей различных четырехугольников»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- S = pr
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- Дипломная работа: Площади многоугольников
- Оглавление
- Введение
- Глава 1. Теоретические основы изучения площадей многоугольников
- 1.1 Вычисление площадей в древности
- 1.2 Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника»
- 1.2.1 Понятие о площади. Свойства площади
- 1.2.2 Понятие о многоугольнике
- 1.2.3 Понятие о площади многоугольника. Дескриптивное определение
- 1.3 Различные формулы площадей многоугольников
- 1.4 Вывод формул площадей многоугольников
- 1.4.1 Площадь треугольника. Формула Герона
- 1.4.2 Площадь прямоугольника
- 1.4.3 Площадь трапеции
- 1.4.4 Площадь четырёхугольника
- 1.4.5 Универсальная формула
- 1.4.6 Площадь n-угольника
- 1.4.7 Вычисление площади многоугольника по координатам его вершин
- 1.4.8 Формула Пика
- 1.5 Теорема Пифагора о сумме площадей квадратов, построенных на катетах прямоугольного треугольника
- 1.6 Равносоставленность треугольников. Теорема Больяя-Гервина
- 1.7 Отношение площадей подобных треугольников
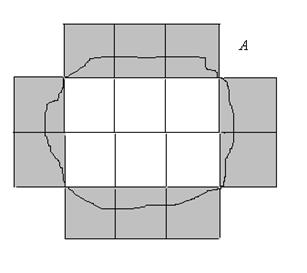
- 1.8 Фигуры с наибольшей площадью
- 1.8.1 Трапеция или прямоугольник
- 1.8.2 Замечательное свойство квадрата
- 1.8.3 Участки другой формы
- 1.8.4 Треугольник с наибольшей площадью
- Глава 2. Методические особенности изучения площадей многоугольников в математических классах
- 2.1 Тематическое планирование и особенности преподавания в классах с углубленным изучением математики
- 2.2 Методика проведения уроков
- 2.3 Результаты опытно-экспериментальной работы
- Заключение
- Литература
- Введение
- Глава 1. Теоретические основы изучения площадей многоугольников
- 1.1Вычисление площадей в древности
- 1.2 Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника»
- 1.2.1 Понятие о площади. Свойства площади
- 1.2.2 Понятие о многоугольнике
- 1.2.3 Понятие о площади многоугольника. Дескриптивное определение
- 1.3 Различные формулы площадей многоугольников
- 1.4 Вывод формул площадей многоугольников
- 1.4.1 Площадь треугольника. Формула Герона
- 1.4.3 Площадь трапеции
- 1.4.4 Площадь четырёхугольника
- 1.4.5 Универсальная формула
- 1.4.6 Площадь n -угольника
- 1.4.7 Вычисление площади многоугольника по координатам его вершин
- 1.4.8 Формула Пика
- 1.5 Теорема Пифагора о сумме площадей квадратов, построенных на катетах прямоугольного треугольника
- 1.6 Равносоставленность треугольников. Теорема Больяя-Гервина
- 1.7 Отношение площадей подобных треугольников
- 1.8Фигуры с наибольшей площадью
- 1.8.1 Трапеция или прямоугольник
- 1.8.3 Участки другой формы
- 1.8.4 Треугольник с наибольшей площадью
- Глава 2. Методические особенности изучения площадей многоугольников в математических классах
- 2.1 Тематическое планирование и особенности преподавания в классах с углубленным изучением математики
- 2.2 Методика проведения уроков
- 2.3 Результаты опытно-экспериментальной работы
- Заключение
- Литература
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат |  | S = a 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
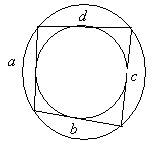
| Произвольный выпуклый четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
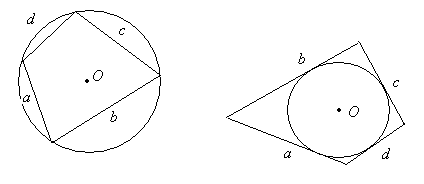
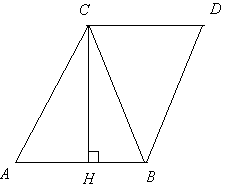
| Вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = a 2 где | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  где | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

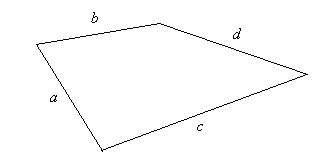
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Вывод формул для площадей четырехугольников
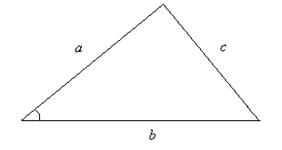
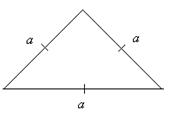
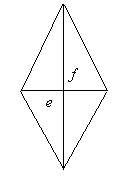
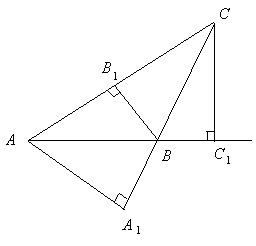
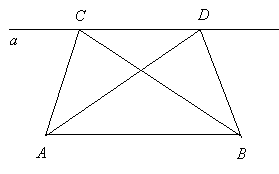
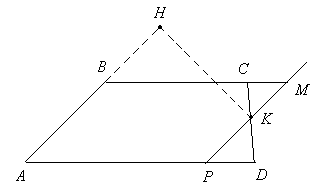
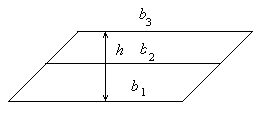
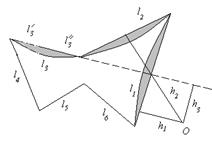
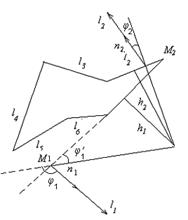
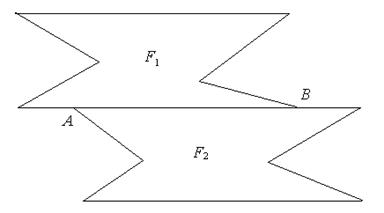
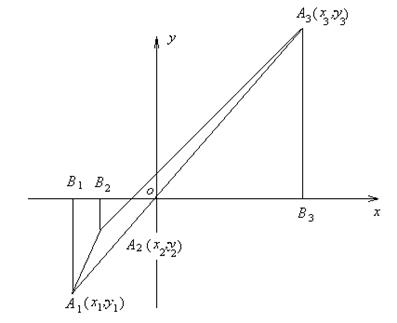
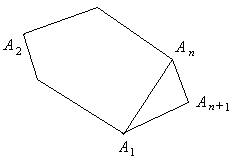
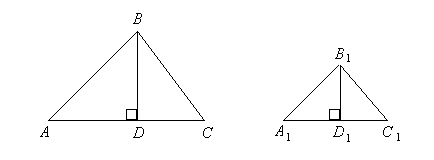
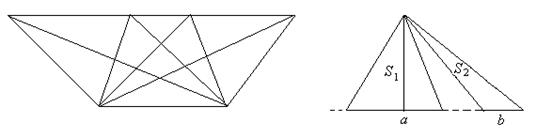
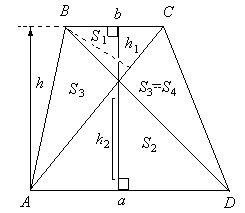
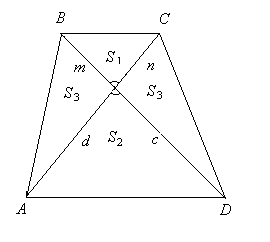
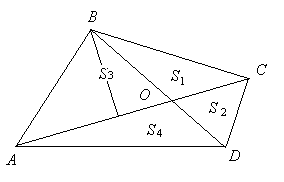
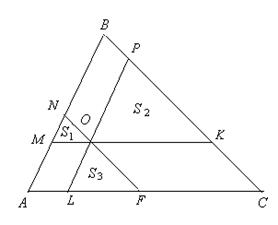
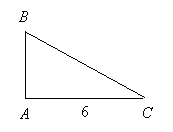
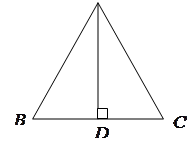
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
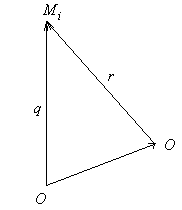
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
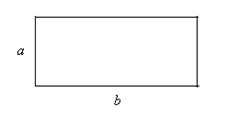
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
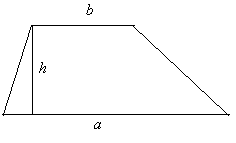
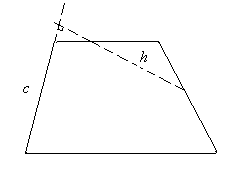
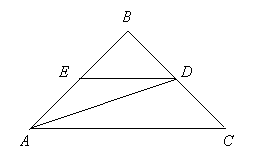
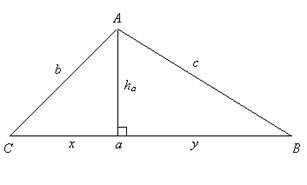
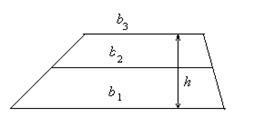
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
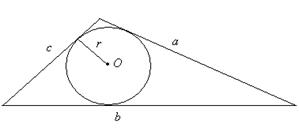
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Видео:Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Информация к проектно-исследовательской работе по теме: «Формулы площадей различных четырехугольников»
Видео:Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
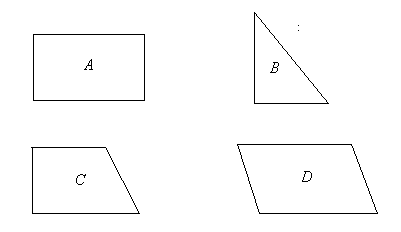
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), не лежащих на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники.
Невыпуклый выпуклый самопересекающийся
описанная окружность трапеция касательный
равнобедренная трапеция параллелограмм выпуклый ромб
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
Выпуклый и невыпуклый четырёхугольники.
Четырёхугольник называется выпуклым, если он лежит по одну сторону от любой прямой, проходящей через любые две его смежные вершины. В противном случае четырёхугольник называется невыпуклым. Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.
Можно найти площадь четырехугольника по этой формуле по диагоналям.
1.3. Основные формулы площадей.
Через диагонали и угол между ними.
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 — диагонали; α — угол между диагоналями
Через стороны и противолежащие углы.
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
S = pr
p — полупериметр четырехугольника; r — радиус вписанной окружности; a, b, c, d — стороны четырехугольника.
Формула площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — Площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмм
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d 1 , d 2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d 1 , d 2 — длины диагоналей.
Формула Герона для трапеции
√ ( p — a )( p — b )( p — a — c )( p — a — d )
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — Площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
Формулы площади выпуклого четырехугольника
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d 1 , d 2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √( p — a )( p — b )( p — c )( p — d ) — abcd cos 2 θ
где S — площадь четырехугольника,
a , b , c , d — длины сторон четырехугольника,
— полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √( p — a )( p — b )( p — c )( p — d )
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 958 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 334 человека из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 683 человека из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Смирнова Нина ФедоровнаНаписать 3477 09.03.2018
Номер материала: ДБ-1299143
- 09.03.2018 211
- 09.03.2018 204
- 09.03.2018 556
- 09.03.2018 762
- 09.03.2018 1326
- 09.03.2018 1678
- 09.03.2018 372
- 09.03.2018 560
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
В России стартует пилотный проект по реабилитации детей-инвалидов
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Россия направит $10,3 млн на развитие школьного питания в нескольких странах
Время чтения: 1 минута
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Дипломная работа: Площади многоугольников
| Название: Площади многоугольников Раздел: Рефераты по математике Тип: дипломная работа Добавлен 22:26:31 24 декабря 2010 Похожие работы Просмотров: 5779 Комментариев: 15 Оценило: 7 человек Средний балл: 4.7 Оценка: 5 Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
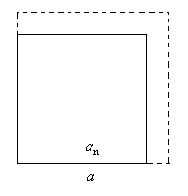
 |
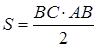

Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной 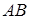
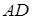
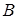
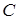
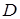
Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.
Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции – произведению полусуммы оснований на высоту.
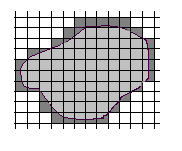
Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на облицовку плиток. Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток – с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.
Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». В своем произведении «Диоптрика» Герон описывает разные машины и практические измерительные инструменты.
Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: « Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая 14 и третья 15. Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
В своем наиболее важном геометрическом произведении «Метрика» Герон излагает доказательство примененной выше формулы:
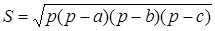
где 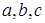
Эта формула носит название «формулы Герона». На самом деле она была установлена еще в 3 в. до н. э. величайшим математиком древности Архимедом.
Практические правила Герона для вычисления площадей применялись греческими, римскими и средневековыми землемерами и техниками.
1.2 Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника»
1.2.1 Понятие о площади. Свойства площади
Обычно говорят, что площадь 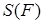
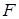
|
Но сколько подобных квадратов нужно, чтобы «составить» круг радиуса 2 см (рис. 1.3, б), совершенно неясно.
 |
|
Строгое математическое определение площади можно получить с помощью палетки – прозрачной пластинки с нанесенной на нее сеткой из равных квадратов. Представим, что такая палетка лежит на плоскости. Иначе говоря, плоскость разбита на квадраты со стороной, равной 1. Если фигура 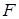
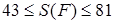
Для большей точности измерения можно каждый квадрат палетки разбить на сто квадратов (стороны которых в 10 раз меньше, чем у квадратов первой палетки, а площадь равна 1/100). Новая, более мелкая палетка даст и более тесные границы, в которых заключена площадь фигуры 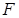
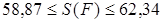
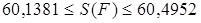
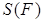
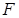
Но здесь есть одна тонкость. Вначале мы получили отрезок 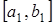
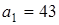
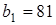
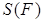
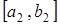
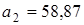
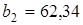
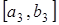
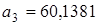
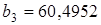
числовой прямой есть либо одна точка (в том случае, когда имеется только одно число 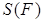
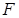
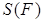
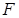
Второй случай, когда пересечение всех отрезков представляет собой отрезок, а не одну точку, на первый взгляд кажется просто невозможным. Ведь всякая фигура имеет какую-нибудь площадь S (F ). Число S (F ) и должно быть единственной общей точкой рассматриваемых отрезков. Но на самом деле это не так. Следующий пример подтверждает это.
Возьмём квадрат Q 1 со стороной 1. Выбросим из него крестообразную фигуру площадью 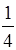
Остаётся фигура Q 2 из четырёх равных квадратов, примыкающих к вершинам Q 1 . (Сторона каждого из них составляет 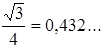

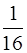
Обозначим через F пересечение всех фигур Q 1 , Q 2 ,Q 3 ,Q 4 , … Другими словами, F получается, если из квадрата Q 1 выбросить по очереди все «кресты». Общая площадь фигур, выбрасываемых из Q 1 , равна 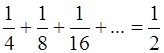
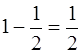
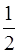
Попробуем теперь измерить площадь фигуры F по Жордану (т. е. с помощью палеток). Какую бы мелкую палетку мы не взяли, площадь фигуры, составленной из квадратов палетки и включающей в себя F , равна нулю (поскольку в F нет ни одного целого квадрата. Таким образом, каждый из получающихся отрезков
(а потому и пересечение всех этих отрезков) содержит отрезок 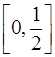
Способ измерения площадей с помощью палеток был предложен в XIX веке французским математиком Камилем Жорданом. Другой французский математик – Анри Лебег предложил более общее определение площади. Построенная выше фигура F неквадрируема по Жордану, но имеет площадь (равную 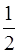
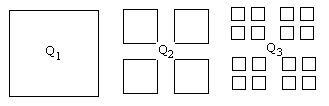
А какие плоские фигуры квадрируемы? Прежде всего многоугольники. Для других фигур применяют следующую теорему:
Плоская фигура F (рис. 1.7) в том и только в том случае квадрируема, если для любого положительного числа 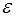
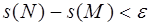
Другими словами, квадрируемы фигуры, которые можно сколь угодно точно приблизить многоугольниками. Например, площадь круга находят как предел площади вписанного в него или описанного около него правильного n-угольника при 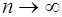
Поскольку обе площади имеют общий предел, их разность стремится к нулю, значит, круг – квадрируемая фигура. Вообще, любая плоская выпуклая фигура квадрируема. Квадрируема и криволинейная трапеция под графиком непрерывной функции 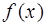
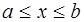
Кроме приведённого выше определения площади с помощью палеток имеется ещё одно, аксиоматическое определение. Прежде чем его сформулировать рассмотрим некоторые свойства площади (будем иметь в виду только площадь по Жордану).
Обозначим через Q множество всех квадрируемых плоских фигур, тогда площадь S (F ) есть числовая функция, определённая на данном множестве. Перечислим свойства, которыми она обладает.
А. Неотрицательность. Площадь любой квадрируемой фигуры F неотрицательна: 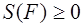
В. Аддитивность. Пусть F 1 и F 2 – две квадрируемые фигуры, у которых нет общих внутренних точек. Обозначим через F объединение этих фигур. Тогда фигура F квадрируема и справедливо равенство 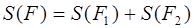
С. Инвариантность. Если две квадрируемые фигуры F 1 и F 2 равны, т. е. одна получается из другой с помощью движения, то площади таких фигур равны: 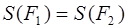
D. Нормируемость. При определении площади фигуры задаётся некоторая единица площади – квадрат К , сторона которого равна динице длины: 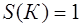
Очевидно, что площадь 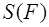
На множестве Q всех квадрируемых фигур существует одна и только одна функция, которая обладает свойствами A, B, C, D.
То есть всякая функция на множестве Q , удовлетворяющая всем четырём свойствам, совпадает с 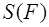
Стало быть, свойства A, B, C, D можно принять за аксиомы площади, т. е. определить площадь как функцию на множестве квадрируемых фигур Q , удовлетворяющую данным аксиомам. Это и есть аксиоматическое определение площади. Все остальные её свойства можно вывести из перечисленных аксиом. Например, формулы для вычисления площадей многоугольников вытекают именно из аксиом A, B, C, D точно так же, как формулы площади круга, эллипса и других фигур.
Заметим, что и в геометрии Лобачевского, и в сферической геометрии площадь определяется теми же аксиомами. Однако палетками пользоваться уже не приходится; за эталон площади принимают не квадрат, а иную фигуру – квадратов на плоскости Лобачевского и сфере просто нет. Интересно, что в обеих геометриях площадь многоугольника пропорциональна разности между суммой его углов и суммой углов плоского многоугольника с тем же числом сторон.
1.2.2 Понятие о многоугольнике
Термин «многоугольник» понимается в математике и, в частности, в школьном курсе математики двояко. Во-первых, многоугольник как линия. В этом случае многоугольник – это простая (т. е. без самопересечения) замкнутая ломаная, лежащая в некоторой плоскости. И, во-вторых, многоугольник, как часть плоскости, ограниченная простой замкнутой ломанной. Эти две трактовки понятия «многоугольник» могут быть использованы самостоятельно в зависимости от характера рассматриваемой задачи. В логическом плане второе понимание термина «многоугольник2 связано с первой теоремой Жордана. В теореме Жордана речь идёт о многоугольнике как о простой замкнутой ломаной.
Каждый многоугольник разбивает все точки плоскости, содержащей этот многоугольник, не принадлежащие самому многоугольнику, на два класса (множества) следующим образом. Любые две точки, принадлежащие одному классу, можно соединить ломаной, не пересекающей многоугольник. И каковы бы ни были две точки, принадлежащие разным классам, — этого сделать нельзя. Один из классов содержит прямые, не пересекающие многоугольник. Множество точек этого класса называют внешней областью многоугольника. Любая прямая, содержащая точки другого класса, пересекает многоугольник и содержит также точки из внешней области многоугольника. Множество точек этого класса называют внутренней областью многоугольника.
Внутренняя область многоугольника вместе с самим многоугольником образует понятие многоугольника во втором смысле (как части плоскости, ограниченной простой замкнутой ломаной).
1.2.3 Понятие о площади многоугольника. Дескриптивное определение
В вопросе о площади многоугольник понимается как часть плоскости, ограниченная простой замкнутой ломаной. В этом смысле понятие «многоугольник» используется в дальнейшем в изложении школьного курса математики, а площадь многоугольника определяется с помощью указания её свойств:
1) численное значение площади любого многоугольника всегда положительно;
2) площади равных многоугольников, т. е. многоугольников, которые можно совместить с помощью движения, одинаковы;
3) площадь многоугольника, полученного объединением двух многоугольников, не имеющих общих внутренних точек, будем называть не перекрывающимися);
4) площадь квадрата со стороной единичной длины равна единице.
В различных учебниках по геометрии для общеобразовательных учреждений определения площади несколько отличаются друг от друга, но суть определений совпадает с указанным выше.
Таким образом, площадь многоугольников можно трактовать как функцию 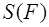
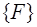
1) неотрицательность площади;
2) аддитивность площади;
3) инвариантность площади;
4) нормированность площади.
Это определение по своему характеру сродни, например, определению арифметического корня 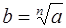
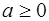
Ведь и в этом случае арифметический корень определяется указанием его свойств. Для корректного определения арифметического корня надо доказать, что такое число b, во-первых, существует и, во-вторых, единственно. Первое следует из того, что множество значений функции
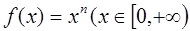
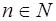
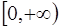
Второе следует из строго монотонного возрастания рассматриваемой функции.
Для корректного определения площади многоугольников – функции 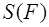
Определения указанного типа носят название дескриптивных (буквально, описательных, от английского слова descriptive – описательный).
Дескриптивные определения отличаются от определений конструктивных (буквально, построительных, от лат. слова construction – построение).
Примером конструктивного определения является, например, определение степени с натуральным показателем: 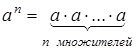
Поборник ознакомления школьников с понятием дескриптивного определения, видный отечественный математик и педагог Я. С. Дубнов, отмечал, что из уравнения, мы имеем дело с дескриптивным определением этого числа, и что концепция дескриптивного определения, как содержащего формулировку некоей задачи, вполне доступна пониманию школьника, стоит только фиксировать его внимание на дескриптивном характере уже знакомых определений. Если этого не делают, то, вероятно, потому, что недооценивают образовательное значение идеи дескриптивного определения, которое одновременно служит инструментом исследования и преддверием к пониманию аксиоматического метода.
Это высказывание более чем сорокалетней давности актуально и сегодня. В школьных учебниках, где фактически программа реализации дескриптивного определения площади многоугольника выполнена полностью (доказаны существование и единственность функции 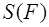
Взгляд на площадь как на первичное понятие сложился ещё в древности. До недавнего времени этого взгляда придерживались и математики. На протяжении многих столетий они видели задачу в вычислении площадей; им не приходило в голову, что «площадь» нуждается в специальном определении.
Между тем их вычисления должны были на чём-то основываться – если не на прямом определении, то на чём-то, его заменяющем, на каких-то принципах, которые позволяли им всякий раз получать в качестве площади определённое число. И такие принципы, конечно, существовали, хотя обычно не формулировались. Это – основные свойства площади. Так, в одних школьных учебниках площадь многоугольников вообще не определяется, но указываются её свойства, соответствующие аксиомам площади. В других же определения носят формально дескриптивный характер, но свойства, определяющие площадь, используются не для построения общей функции 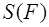
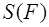
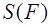
1.3 Различные формулы площадей многоугольников
Площадь прямоугольника со сторонами 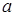
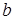
Площадь параллелограмма вычисляется по формулам
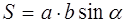
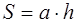
где а – его основание, b – боковая сторона, α – угол между ними, h – высота (рис. 19)
Площадь многоугольника вычисляется по формулам
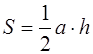
где а – одна из сторон треугольника, h – проведённая к ней высота (рис. 1.10, а );
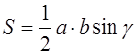
где a , b – стороны треугольника, γ – угол между ними (рис 1.10, а);
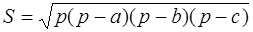
где а, b , с – стороны треугольника, а 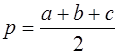
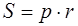
где р – полупериметр, r – радиус вписанной в треугольник окружности (рис. 1.10, в);
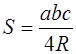
где a , b , c – стороны треугольника, R – радиус описанной около треугольника окружности (рис. 1.10, г);
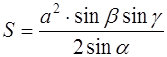
где 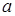
Площадь правильного треугольника вычисляется по формуле
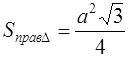
где 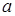
Площадь трапеции вычисляется по формулам
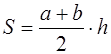
где а и b – основания трапеции, h – высота (рис. 1.11, а);
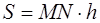
где MN – средняя линия трапеции, h – её высота (рис. 1.11, б);
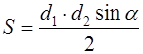
где d 1 , d 2 – диагонали трапеции, α – угол между ними (рис. 1.11);
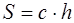
где с – боковая сторона трапеции, 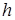
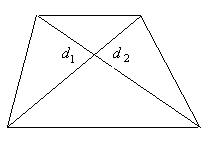
Если даны диагонали e и f и угол α между ними, то площадь произвольного четырёхугольника находят по формуле
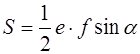
В частности, площадь ромба равна полупроизведению его диагоналей (рис. 1.12):
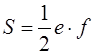
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b , c и сумму 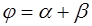

где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника (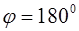
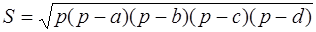
а описанного (рис. 1.14, б) (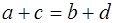
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
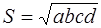
Площадь всякого описанного многоугольника вычисляется по формуле
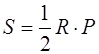
где R – радиус круга, вписанного в многоугольник, а Р – периметр прямоугольника.
Общий метод для нахождения площади произвольного многоугольника состоит в том, что его надо разбить на треугольники, вычислить их площади и сложить результаты. Иногда многоугольник представляют как сумму и разность треугольников. Однако простой и компактной формулы для определения площади произвольного n -угольника нет. Это неудивительно, ведь в ней неизбежно будет слишком много переменных. Чтобы задать n -угольник (его форму и размеры), нужно указать 2n – 3 его элемента: например, длины всех сторон. Кроме одной, и величины n – 2 образованных ими углов.
1.4 Вывод формул площадей многоугольников
1.4.1 Площадь треугольника. Формула Герона
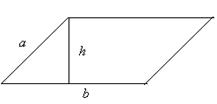
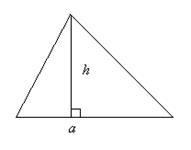
Теорема . Площадь треугольника равна половине произведения его стороны на проведённую к ней высоту:
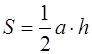
Доказательство проводится очень просто. Данный треугольник АВС (рис. 1.15) достроим до параллелограмма ABDC . Треугольники ABC и DCB равны по трём сторонам, поэтому их площади равны. Значит площадь треугольника АВС равна половине площади параллелограмма ABDC , т. е.
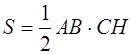
Но здесь возникает следующий вопрос: почему три возможных полупроизведения основания на высоту для всякого треугольника одинаковы? Это, впрочем, легко доказать из подобия прямоугольников с общим острым углом. Рассмотрим треугольник АВС (рис. 1.16):
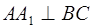
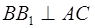
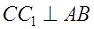
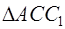
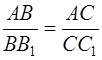
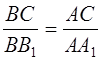
откуда 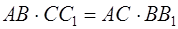
и 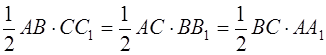
Однако в школьных учебниках так не делается. Наоборот, равенство трёх полупроизведений устанавливается на основе того, что все эти полупроизведения выражают площадь треугольника. Таким образом, неявно используется существование единственной функции 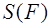
Пользуясь приведённой выше теоремой о площади треугольника очень часто бывает удобно сравнивать площади двух треугольников. Приведём ниже некоторые очевидные, но важные следствия из теоремы.
Следствие 1 . Если вершину треугольника передвигать по прямой, параллельной её основанию, то его площадь при этом не меняется.
На рис. 1.17 треугольники АВС и АВ D имеют общее основание АВ и равные высоты, опущенные на это основание, т. к. прямая а , которая содержит вершины С и D параллельна основанию АВ , а поэтому площади этих треугольников равны.
Следствие 1 можно переформулировать следующим образом.
Следствие 1′ . Пусть дан отрезок АВ . Множество точек М таких, что площадь треугольника АМВ равна заданной величине S , есть две прямые, параллельные отрезку АВ и находящиеся от него на расстоянии 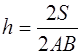
Следствие 2 . Если одну из сторон треугольника, прилежащих к данному его углу, увеличить в k раз, то площадь его также увеличится в k раз.
На рис. 1.19 треугольники АВС и ABD имеют общую высоту В H , поэтому отношение их площадей равно отношению оснований
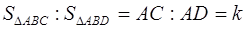
Из следствия 2 следуют важные частные случаи:
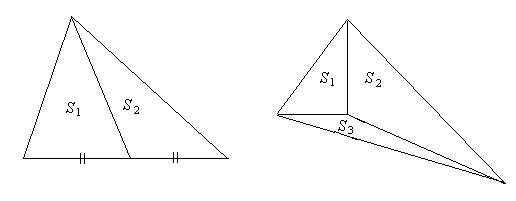
1. Медиана делит треугольник на две рановеликие части.
2. Биссектриса угла треугольника, заключённая между его сторонами а и b , делит его на два треугольника, площади которых относятся как a : b .
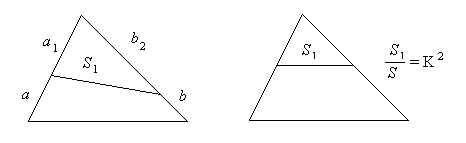
Следствие 3 . Если два треугольника имеют общий угол, то их площади относятся как произведения сторон, заключающих этот угол.
Это следует из того, что (рис. 1.19)
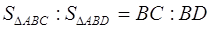
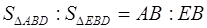
поэтому 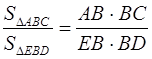
В частности, имеет место следующее утверждение:
Если два треугольника подобны и сторона одного из них в k раз больше соответствующих сторон другого, то его площадь в k 2 раз больше площади второго.
Выведем формулу Герона для площади треугольника следующими двумя способами. В первом используем теорему косинусов:
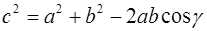
где a , b , c – длины сторон треугольника, γ – угол, противолежащий стороне с .
Из (1.3) находим 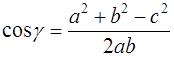
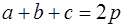
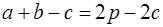
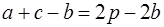
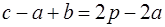
где 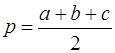
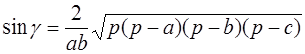
Таким образом, площадь треугольника
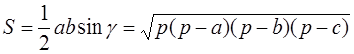
Формулу Герона можно вывести, опираясь только на теорему Пифагора и не используя теорему косинусов.
Рассмотрим произвольный треугольник АВС (рис. 1.20) со сторонами a , b , c .
В нём всегда найдётся высота, основание которой лежит на стороне треугольника, а не на её продолжении. Искомая площадь треугольника АВС :
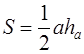
следовательно, для её определения достаточно вычислить 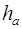
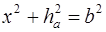

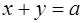
Решаем полученную систему трёх уравнений с тремя неизвестными 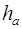
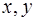
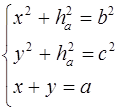
Вычитая из первого уравнения системы (1.4) второе, имеем:
Теперь из первого уравнения системы (1.4) находим 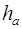
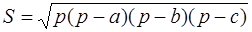
Предложенный вывод формулы Герона отражает межпредметные связи алгебры и геометрии, он доступен учащимся сразу же после изучения теоремы Пифагора.
Теорема . Площадь прямоугольника равна произведению его смежных сторон.
Рассмотрим одно из доказательств этой теоремы, которое в школьном курсе не рассматривается.
Пусть нам дан прямоугольник со сторонами a , b и площадью S (рис. 1.21). Докажем, что
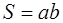
Достроим прямоугольник до квадрата со стороной a + b . Площадь этого квадрата 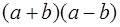
С другой стороны, этот квадрат составлен из данного прямоугольника с площадью S , равного ему прямоугольника с площадью S и двух квадратов с площадями
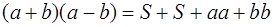
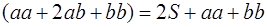
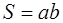
1.4.3 Площадь трапеции
Докажем следующую формулу для вычисления площади трапеции:
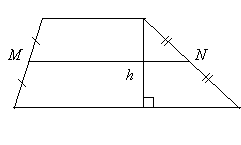
Площадь трапеции равна произведению одной из боковых сторон на длину перепендикуляра, опущенного на неё из середины другой боковой стороны.
Доказательство. Пусть ABCD – данная трапеция (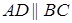
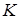
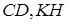
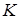
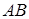
Проведём через точку K прямую, параллельную прямой АВ . Пусть М и Р – точки её пересечения с прямыми ВС и AD . Параллелограмм АВМР равновелик данной трапеции, так как пятиугольник АВСКР является для них общим, а треугольник СМК конгруэнтен треугольнику KPD , т. е. трапеция и параллелограмм составлены из одинаковых частей.
Поскольку площадь параллелограмма равна произведению его основания АВ на высоту КН , утверждение доказано.
Замечание . Последний абзац решения можно (более формально) записать и так:
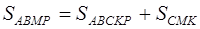
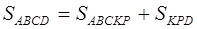
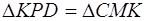
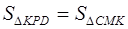
следовательно, 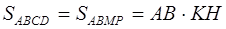
1.4.4 Площадь четырёхугольника
Школьная программа предусматривает вычисление площадей фактически двух видов выпуклых четырёхугольников: параллелограмма и трапеции. Для четырёхугольника, фактически не являющегося параллелограммом или трапецией, формула нахождения его площади не выводится. В то же время применение такой формулы для решения ряда задач было бы удобным. Имеется в виду формула вычисления площади произвольного выпуклого четырёхугольника, которую можно назвать аналогом формулы Герона, учитывая их некоторое внешнее свойство.
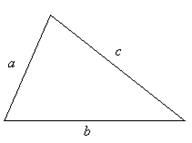
Докажем следующую теорему : площадь произвольного выпуклого четырёхугольника может быть определена по формуле:
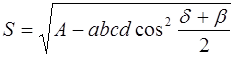
где 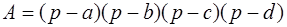
Доказательство. Пусть в четырёхугольнике ABCD АВ = а , ВС = b ,
Из 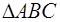
Из 
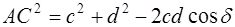
Приравнивая правые части этих выражений, получим:
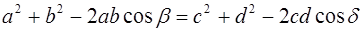
или 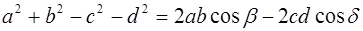
Найдём площадь четырёхугольника ABCD как сумму площадей треугольников ABC и ADC :
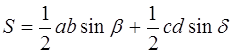
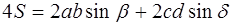
В равенствах (1.5) и (1.6) обе части возведём в квадрат, а затем почленно сложим:
Выполним равносильные преобразования, получим
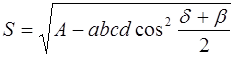
что и требовалось доказать.
Теорема имеет ряд следствий.
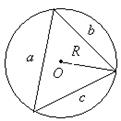
Следствие 1 . Площадь произвольного четырёхугольника, вписанного в окружность, вычисляется по формуле (как было сказано выше) Брахмагупты:
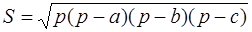
Доказательство сразу следует из теоремы, рассмотренной выше, с учётом того, что сумма противолежащих углов вписанного в окружность четырёхугольника равна 180 0 , т. е.
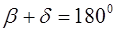
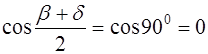
Поэтому 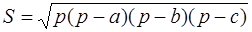
Следствие 2 . Площадь произвольного четырёхугольника, описанного около окружности, вычисляется по формуле:
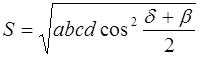
Доказательство. Так как у описанного четырёхугольника суммы противолежащих сторон равны, т. е.
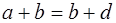
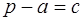
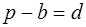
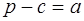
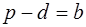
Следствие 3 . Площадь четырёхугольника, вписанного в окружность и описанного около окружности, может быть вычислена по формуле:
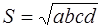
Доказательство. Так как 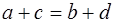
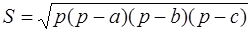
то
1.4.5 Универсальная формула
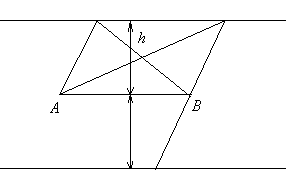
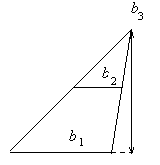
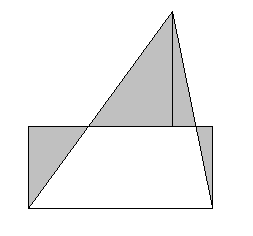
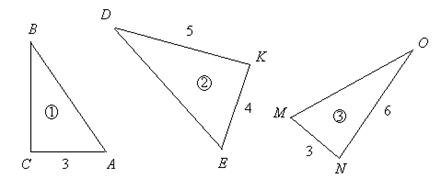
Существует универсальная формула, известная в математике под названием формулы Симпсона, с помощью которой можно вычислять площади плоских фигур: параллелограмма, трапеции и треугольника.
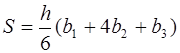
где 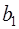
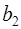
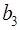
Применяя формулу, имеем:
Для параллелограмма (квадрата, прямоугольника) (рис. 6, а)
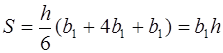
для трапеции (рис 6, б)
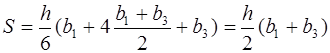
для треугольника (рис 6, в)
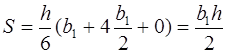
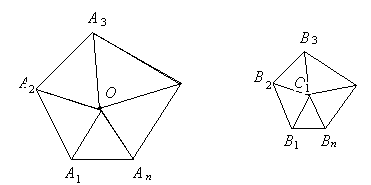
1.4.6 Площадь n -угольника
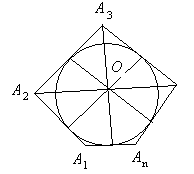
Теорема . Площадь всякого описанного многоугольника равна произведению периметра на половину радиуса.
Доказательство. Соединив центр О (рис. 1.25) со всеми вершинами описанного многоугольника, разделим его на треугольники, в которых за основания можно взять стороны многоугольника, а за высоты – радиус круга.
Обозначив этот радиус через R , будем иметь:
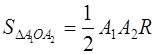
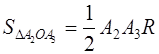
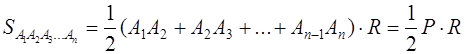
где Р – периметр прямоугольника.
Следствие . Площадь правильного многоугольника равна произведению периметра на половину апофемы, т. к. всякий правильный многоугольник можно рассматривать как описанный около круга, у которого радиус есть апофема.
Для нахождения площади какого-нибудь неправильного многоугольника нужно его разбить на треугольники, вычислить площадь каждого треугольника в отдельности и результаты сложить. Но здесь возникает следующий вопрос: почему при различных разбиениях многоугольника на треугольники соответствующие суммы окажутся одинаковыми? Если бы это было доказано, то при условии единственности площади прямоугольника (произведения длин его сторон) тем самым была бы построена единственная функция 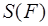
Метод, о котором далее пойдёт речь был впервые применён французским математиком Жераром в 1895 году и усовершенствован Лебегом.
Отыскание функции 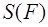
I. Выбираем на плоскости произвольную точку О . Указываем выражение 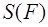
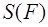
Пусть 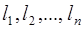
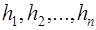
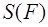
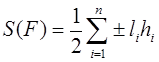
где ставится знак «+», если прилегающая к стороне 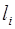
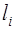
Отметим, что значение 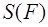
Так, например (рис. 1.26),
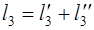
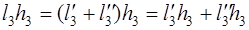
причём знаки перед выражениями 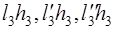
Формула (1.7) может быть записана в векторной форме. Обозначим через 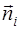
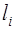
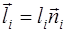
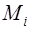
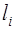
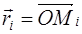
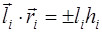
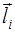
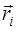
Доказательство проведём для двух сторон прямоугольника, у которых произведение 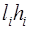
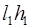
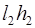
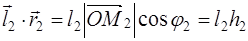
Для остальных сторон соотношение 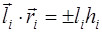
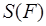
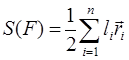
II. Докажем, что величина 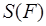
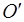
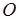
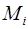
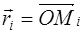
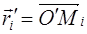
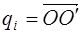
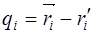
Для произвольного многоугольника найдём разность значений функции 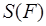
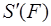
Введём вектор 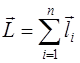
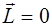
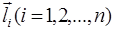


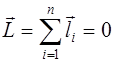
Из полученного равенства следует, что
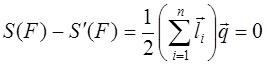
Таким образом, величина 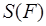
III. Покажем, что значения 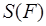
Пусть точка О находится в одной из вершин прямоугольника F со сторонами a и b , тогда сумма (1.7) состоит из двух положительных слагаемых 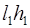
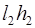
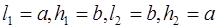
В частности, если 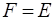
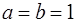
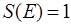
Если точку О поместить в вершину А треугольника F , равного треугольнику АВС , то получим обычную формулу площади треугольника
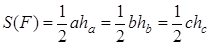
IV. Покажем, что 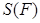
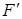
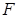
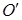
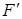
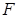
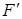
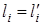
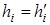
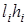
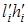
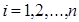
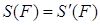
V. Докажем, что 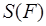
Возьмём прямоугольник 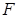
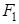
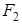
Общей частью многоугольников 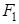
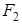
Используем формулу (1.7′). Вклады отрезка АВ в суммы 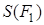
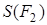
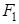
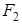
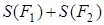
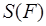
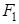
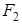
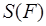
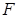
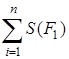
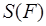
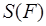
Итак, функция 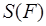
1.4.7 Вычисление площади многоугольника по координатам его вершин
Метод координат, предложенный в XVII веке французскими математиками Р. Декартом (1596-1650) и П. Ферма (1601-1665), является мощным аппаратом, позволяющем переводить геометрические понятия на алгебраический язык. В основе этого метода лежит понятие – система координат. Мы будем рассматривать вычисление площади многоугольника по координатам его вершин в прямоугольной системе координат.
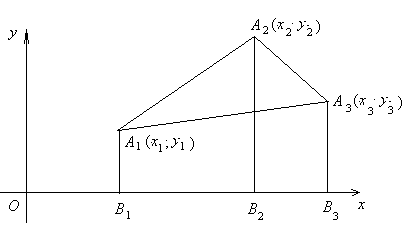
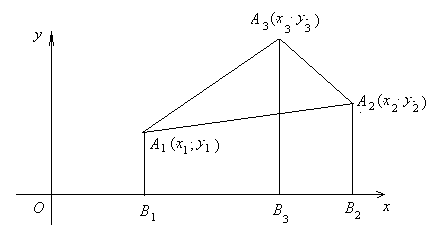
Теорема 1 . Если 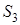
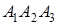
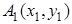
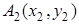
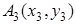
то справедливо равенство
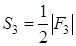
где 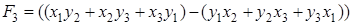
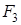
Доказательство. Пусть вершины 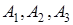
Случай 1 . Направление 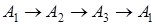
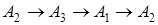
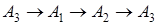
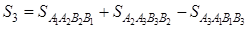
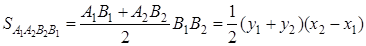
Так как фигура 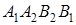
Аналогично находим, что
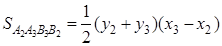
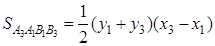
Выполнив алгебраические преобразования
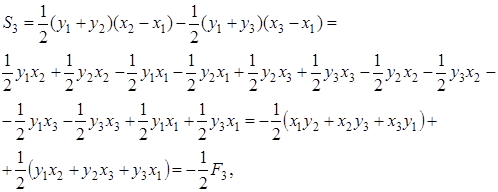
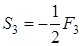
В равенстве (1.9) определитель площади 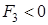
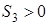
Покажем, что 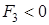
(площадь прямоугольника с основанием 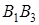
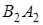
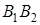
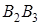
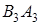
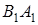
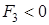
Случай 2 . Указанные направления в случае 1 противоположны направлению движения конца часовой стрелки (рис. 1.31)
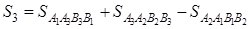
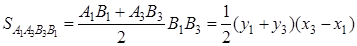
так как фигура 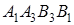
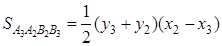
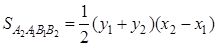
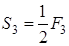
где 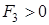
Теорема доказана, когда вершины треугольника расположены в первой координатной четверти.
Воспользовавшись понятием модуля, равенства (1.9) и (1.10) можно записать так:
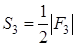
Замечание 1 . Мы вывели формулу (1.8), рассматривая простейшее расположение вершин 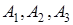
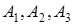
Рассмотрим случай, изображённый на рисунке 1.32.
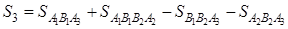
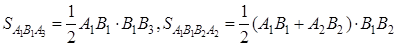
где
Поэтому, выполнив несложные геометрические преобразования:
получим снова, что 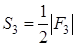
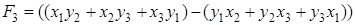
Многоугольник может быть выпуклым или невыпуклым, порядок нумерации вершин считается отрицательным, если вершины нумеруются по направлению движения конца часовой стрелки. Многоугольник, не имеющий самопересечения сторон, будем называть простым. Для простого именно n -угольника справедлива следующая
Теорема 2 . Если 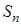
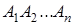
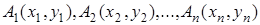
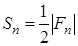
где
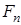
Доказательство. Возможны два случая.
Случай 1 . n -угольник – выпуклый. Докажем формулу (1.11) методом математической индукции.
Для 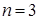
Добавим к многоугольнику 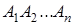
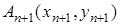
Таким образом, формула справедлива для (n +1)-угольника, и, значит, условия математической индукции выполнены, т. е. формула (1.11) для случая выпуклого n -угольника доказана.
Случай 2 . n -угольник – невыпуклый.
В любом невыпуклом n -угольнике можно провести диагональ, лежащую внутри него, и поэтому доказательство случая 2 для невыпуклого n -угольника аналогична доказательству для выпуклого n -угольника.
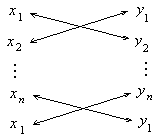
Замечание 2 . Выражения для 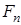
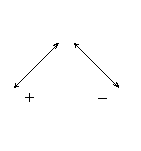
Знаки в столбце (1.12) надо расставить так, как указано в схеме (1.13).
Замечание 3 . При составлении столбца (1.12) для треугольника можно начать с любой вершины.
Замечание 4 . При составлении столбца (1.12) для n -угольника (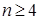
1.4.8 Формула Пика
Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, 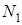
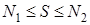
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где 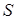
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
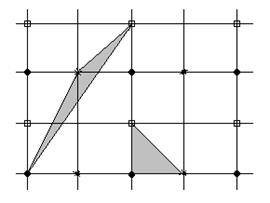
Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Проделав это, например, для треугольников, изображённых на рисунке 1.34, можно убедиться, что площадь получается всегда равной «полученному» числу – числу вида 
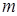
Назовём треугольник простым, если ни внутри него, ни на его сторонах нет узлов сетки, за исключением вершин. Все простые треугольники на рис. 1.34 имеют площадь 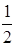
Задача . Три кузнечика (три точки) в начальный момент времени сидят в трёх вершинах одной клетки, а затем начинают «играть в чехарду»: каждый может прыгнуть через одного из двух других, после чего оказывается в симметричной относительно его точке (рис. 1.35, ясно, что после любого числа таких прыжков кузнечики будут попадать в узлы клетчатой бумаги). В каких тройках точек могут через несколько прыжков оказаться кузнечики?
Назовём треугольник достижимым, если в его вершинах могут одновременно оказаться три кузнечика, которые вначале были в трёх вершинах одной клетки; прыжком будем называть преобразование треугольника, заключающееся в том, что одна из вершин переходит в точку, симметричную относительно любой из двух других вершин (эти две вершины остаются на месте).
Теорема 1 . Следующие три свойства треугольников с вершинами в узлах клетчатой бумаги эквивалентны друг другу:
1) треугольник имеет площадь 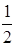
2) треугольник прост,
3) треугольник достижим.
Познакомимся со следующими свойствами простого треугольника, которые и приводят к справедливости данной теоремы.
1. Площадь треугольника при прыжке не меняется.
2. Любой достижимый треугольник имеет площадь 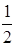
3. Если достроить простой треугольник АВС до параллелограмма ABCD , то ни внутри, ни на сторонах этого параллелограмма не будет узлов (не считая вершин).
4. Из простого треугольника при прыжке получается простой.
5. Из простого треугольника один из углов – тупой или прямой (причём последний случай возможен только для треугольника, у которого три вершины принадлежат одной клетке, такой простой треугольник – со сторонами 1, 1, 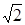
6. Из любого простого не минимального треугольника можно одним прыжком получить треугольник, у которого наибольшая сторона меньше, чем наибольшая сторона исходного.
7. Любой простой треугольник можно конечным числом прыжков перевести в минимальный.
8. Любой простой треугольник достижим.
9. Любой простой треугольник имеет площадь 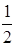
10. Любой треугольник можно разрезать на простые.
11. Площадь любого треугольника равна 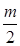
12. Любой треугольник площади 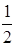
13. Для любых двух узлов А и В решётки, на отрезке между которыми нет других узлов, найдётся узел С такой, что треугольник АВС – простой.
14. Узел С в предыдущем свойстве можно всегда выбрать так, что угол АСВ будет тупым или прямым.
15. Пусть клетчатая плоскость разрезана на равные параллелограммы так, что все узлы являются вершинами параллелограммов. Тогда каждый из треугольников, на которые один из этих параллелограммов разрезается своей диагональю – простой.
16. (Обратное 15). Треугольник АВС – простой тогда и только тогда, когда всевозможные треугольники, полученные из АВС параллельными переносами, переводящими узел А в различные узлы решётки, не накладываются друг на друга.
17. Если решётку – узлы клетчатой бумаги – разбить на четыре подрешётки с клетками 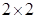
Следующие два свойства дают ответ к задаче о трёх кузнечиках.
18. Три кузнечика могут одновременно попасть в те и только те тройки точек, которые служат вершинами простого треугольника и имеют тот же знак, что и соответствующие вершины начального треугольника.
19. Два кузнечика могут одновременно попасть в те и только те пары узлов соответствующих знаков, на отрезке между которыми нет других узлов.
Мы рассмотрим частный вид многоугольников на клетчатой бумаге, которому в формуле Пика соответствуют значения 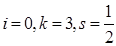
Пусть на плоскости задан некоторый многоугольник и некоторое конечное множество К точек, лежащих внутри многоугольника и на его границе (причём все вершины многоугольника принадлежат множеству К ).
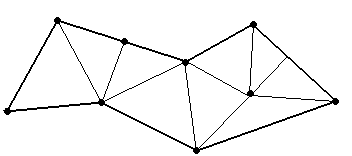
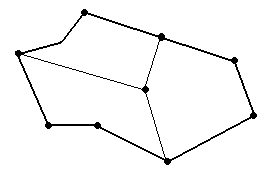
Триангуляцией с вершинами К называется разбиение данного многоугольника на треугольники с вершинами в множестве К такое, что каждая точка из К служит вершиной каждому из тех треугольников триангуляции, которым эта точка принадлежит (то есть точки из К не попадают внутрь или на стороны треугольников, рис. 1.37).
Теорема 2 . а) Любой n -угольник можно разрезать диагоналями на треугольники, причём количество треугольников будет равно n – 2 (это разбиение – триангуляция с вершинами в вершинах n -угольника).
б) Пусть на границе многоугольника отмечено r точек (включая все вершины), внутри – ещё i точек. Тогда существует триангуляция с вершинами в отмеченных точках, причём количество треугольников такой триангуляции будет равно 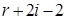
Разумеется, а) – частный случай б), когда 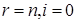
Справедливость этой теоремы следует из следующих утверждений.
1) Из вершины наибольшего угла n -угольника (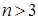
2) Если n -угольник разрезан диагональю на р -угольник и q -угольник, то 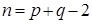
3) Сумма углов n -угольника равна 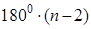
4) Любой n -угольник можно разрезать диагоналями на 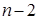
5) Для любого треугольника, внутри и на границе которого отмечены несколько точек (в том числе и все три его вершины), существует триангуляция с вершинами в отмеченных точках.
6) То же самое верно и для любого n -угольника.
7) Число треугольников триангуляции равно 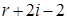
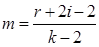
9) Если 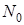
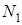
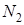
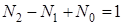
Из теорем 1 и 2 и вытекает формула Пика:
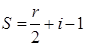
1.5 Теорема Пифагора о сумме площадей квадратов, построенных на катетах прямоугольного треугольника
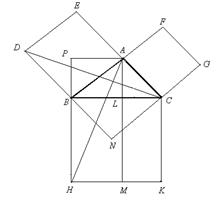
Теорема . Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе этого треугольника .Доказательство. Пусть АВС (рис. 1.39) – прямоугольный треугольник, а BDEA , AFGE и BCKH – квадраты, построенные на его катетах и гипотенузе; требуется доказать, что сумма площадей двух первых квадратов равна площади третьего квадрата.
Проведём 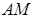
Проведём вспомогательные прямые DC и АН . Рассмотрим треугольники DCB и ABH . Треугольник DCB , имеющий основание BD , общее с квадратом BDEA , а высоту С N , равную высоте АВ этого квадрата, равновелик половине квадрата. Треугольник АВН , имеющий основание ВН , общее с прямоугольником BLMH , и высоту АР , равную высоте BL этого прямоугольника, равновелик его половине. Сравнивая эти два треугольника между собой, находим, что у них BD = ВА и ВС = ВН (как стороны квадрата);
Сверх того, ÐDCB = ÐАВН , т. к. каждый из этих углов состоит из общей части — ÐАВС и прямого угла. Значит, треугольники АВН и ВС D равны. Отсюда следует, что прямоугольник BLMN равновелик квадрату BDEA . Точно также доказывается, что прямоугольник LGKM равновелик квадрату AFGC . Отсюда следует, что квадрат ВСКН равновелик сумме квадратов BDEA и AFGC .
1.6 Равносоставленность треугольников. Теорема Больяя-Гервина
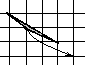
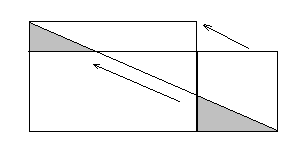
Немало формул и теорем в геометрии доказывается с помощью разрезания фигур, а затем перекладывания их частей – вспомним, например, теорему Пифагора. Если две фигуры можно разрезать на одинаковые наборы частей (т. е. между частями из таких наборов можно установить взаимнооднозначное соответствие, при котором соответственные части равны), то эти фигуры называются равносоставленными. Равносоставленные фигуры, разумеется, равновелики – они имеют равные площади. Для многоугольников верна и обратная теорема: любые два равновеликих многоугольников равносоставлены. В 1832 г. Её доказал венгерский математик Фаркаш Больяй, а годом позже, но независимо от него, немец П. Гервин. Ключ к доказательству – перекройка прямоугольника, показанная на рисунке 1.40: разрезав «низкий» прямоугольник на два треугольника и пятиугольник, сдвинув треугольники вдоль наклонной линии разреза, мы получаем другой, «высокий» прямоугольник.
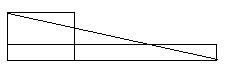
Этим способом данный прямоугольник не трудно превратить почти в любой другой равновеликий ему – надо только, чтобы новый прямоугольник был «выше» исходного, но не более, чем вдвое. Если же отношение высот прямоугольников больше двух (рис. 1.41, а), «низкий» можно «сделать повыше» с помощью простого преобразования (рис. 1.41, б), применённого нужное число раз.
Теперь любой многоугольник мы сумеем перекроить в прямоугольник какой-то фиксированной высоты h : разрежем его на треугольники, каждый треугольник превратим в прямоугольник (рис. 1.42), приведём полученные прямоугольники к некоторой постоянной высоте h и состыкуем вертикальными сторонами.
Если два треугольника равновелики, то соответствующие им прямоугольники к некоторой постоянной высоте h равны. Таким образом, эти многоугольники равносоставлены с одной и той же фигурой, а отсюда уже заключаем, что они равносоставлены между собой.
1.7 Отношение площадей подобных треугольников
Теорема 1 . Площади двух треугольников, имеющих по равному углу, относятся, как произведения сторон, заключающих эти углы.
Доказательство. Пусть в треугольниках АВС и 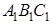
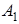
Проведя высоты 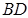
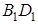
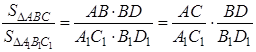
Треугольники 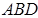
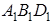
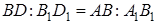
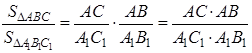
Теорема 2 . Площади подобных многоугольников относятся как квадраты сходственных сторон.
Доказательство. 1) Если 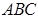
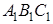
Применим к ним предыдущую теорему:
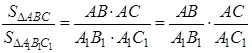
Но из подобия треугольников следует:
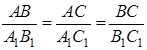
Поэтому в равенстве (1.14) мы можем каждое из отношений 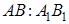
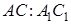
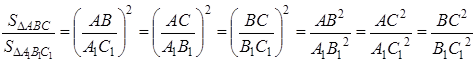
2) Если 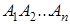
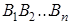
Пусть эти треугольники будут:
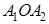
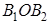
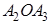
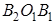
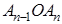
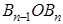
Согласно доказанному в первой части этой теоремы, получим пропорции:
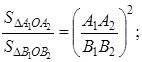
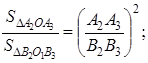
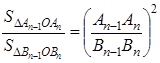
Но из подобия многоугольников следует:
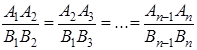
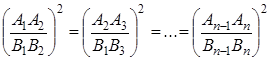

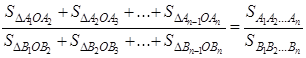
Следствие . Площади правильных одноимённых многоугольников относятся как квадраты сторон, или как квадраты радиусов апофем.
1.8Фигуры с наибольшей площадью
1.8.1 Трапеция или прямоугольник
Рассмотрение этого пункта начнём с решения задачи.
Задача . В роковой в своей жизни день Пахом прошёл 40 вёрст, идя по сторонам трапеции площадью 78 квадратных вёрст. Его первоначальным намерением было идти по сторонам прямоугольника, трапеция же получилась случайно, в результате плохого расчёта. Интересно определить: выгадал он или прогадал от того, что участок его оказался не прямоугольником, а трапецией? В каком случае должен он был получить большую площадь земли?
Решение. Прямоугольников с обводом в 40 вёрст может быть очень много, и каждый имеет другую площадь.
Вот ряд примеров:
14 × 6 = 84 кв. вёрст
13 × 7 = 91 кв. вёрст
12 × 8 = 96 кв. вёрст
11 × 9 = 99 кв. вёрст
Мы видим, что у всех этих фигур при одном и том же периметре в 40 вёрст площадь больше, чем у нашей трапеции. Однако возможны и такие прямоугольники с периметром в 40 вёрст, площадь которых меньше, чем у трапеции:
18 × 2 = 36 кв. вёрст
19 × 1 = 19 кв. вёрст
19,5 × 0,5 = 9,75 кв. вёрст.
Следовательно, на вопрос задачи нельзя дать определённого ответа. Есть прямоугольники с большей площадью, чем трапеция, но есть и с меньшей, при одном и том же обводе. Зато можно дать вполне определённый ответ на вопрос: какая из всех прямоугольных фигур с заданным периметром заключает самую большую площадь? Сравнивая наши прямоугольники, замечаем, что чем меньше разница в длине сторон, тем площадь прямоугольника больше. Естественно заключить, что когда этой разницы не будет вовсе, т. е. когда прямоугольник превратится в квадрат, площадь фигуры достигнет наибольшей величины. Она будет равна тогда 10 × 10 = 100 кв. вёрст. Легко видеть, что этот квадрат действительно превосходит по площади любой прямоугольник одинакового с ним периметра. Пахому следовало идти по сторонам квадрата, чтобы получить участок наибольшей площади, — на 22 квадратной версты больше, чем он успел охватить.
Замечательное свойство квадрата – заключать в своих границах наибольшую площадь по сравнению со всеми другими прямоугольниками того же периметра. Приведём строгое доказательство.
Обозначим периметр прямоугольной фигуры через Р . Если взять квадрат с таким периметром, то каждая сторона его должна равняться 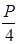
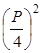
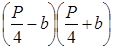
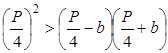
Так как правая сторона этого неравенства равна 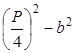
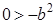
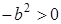
Но последнее неравенство очевидно: квадрат всякого количества, положительного или отрицательного, больше нуля. Следовательно, справедливо и первоначальное равенство, которое привело нас к этому.
Итак, квадрат имеет наибольшую площадь из всех прямоугольников с таким же периметром.
Отсюда следует и то, что из всех прямоугольных фигур с одинаковыми площадями квадрат имеет наименьший периметр. В этом можно убедиться следующим рассуждением. Допустим, что это не верно и что существует такой прямоугольник А , который при равной с квадратом В площади имеет периметр меньший, чем у него. Тогда, начертив квадрат С того же периметра, как у прямоугольника А , получим квадрат имеющий большую площадь, чем у А , и, следовательно, большую, чем у квадрата В . В итоге получили, что квадрат С имеет периметр меньший, чем квадрат В , а площадь большую, чем он. Это, очевидно, невозможно: раз сторона квадрата С меньше, чем сторона квадрата В , то и площадь должна быть меньше. Значит нельзя было допустить существование прямоугольника А , который при одинаковой площади имеет периметр меньший, чем у квадрата. Другими словами, из всех прямоугольников с одинаковой площадью наименьший периметр имеет квадрат.
Знакомство с этими свойствами квадрата помогло Пахому правильно рассчитать свои силы и получить прямоугольный участок наибольшей площади. Зная, что он может пройти в день без напряжения, например, 36 вёрст, он пошёл бы по границе квадрата со стороной 9 вёрст и к вечеру был бы обладателем участка в 81 квадратную версту, — на 3 квадратные версты больше, чем он получил со смертельным напряжением сил. И, наоборот, если бы он наперёд ограничился какой-нибудь определённой площадью прямоугольного участка, например, в 36 квадратных вёрст, то мог бы достичь результата с наименьшей затратой сил, идя по границе квадрата, сторона которого — 6 вёрст.
1.8.3 Участки другой формы
Но, может быть, Пахому ещё выгоднее было бы выкроить себе участок вовсе не прямоугольной формы, а какой-нибудь другой – четырёхугольной, треугольной, пятиугольной и т. д.
Познакомимся со следующими утверждениями, которые и отвечают на поставленный вопрос.
Во-первых, из всех четырёхугольников с одинаковым периметром наибольшую площадь имеет квадрат. Поэтому, желая иметь четырёхугольный участок, Пахом никакими ухищрениями не мог бы овладеть более чем 100 квадратными вёрстами (считал, что максимальный дневной пробег его – 40 вёрст).
Во-вторых, квадрат имеет большую площадь, чем всякий треугольник равного периметра. Равносторонний треугольник такого же периметра имеет сторону 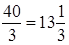
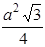
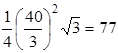
Но если будем сравнивать площадь квадрата с площадью пятиугольника, шестиугольника и т. д. равного периметра, то здесь неравенство его прекращается: правильный пятиугольник обладает наибольшей площадью, правильный шестиугольник – ещё большей, и т. д. Легко убедиться в этом на примере правильного шестиугольника. При периметре в 40 вёрст его сторона 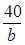
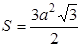
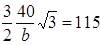
Избери Пахом для своего участка форму правильного шестиугольника, он при том же напряжении сил овладел бы площадью на 115 -78, т. е. на 37 квадратных вёрст больше, чем в действительности, и на 15 квадратных вёрст больше, чем дал бы ему квадратный участок.
1.8.4 Треугольник с наибольшей площадью
Мы уже заметили раньше, что из всех треугольников с равными периметрами равносторонний обладает наибольшей площадью. Докажем это.
Площадь S треугольника со сторонами а, b , с и периметром 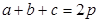
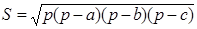
Площадь S треугольника будет наибольшей тогда же, когда станет наибольшей величиной и её квадрат 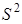
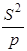
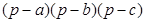
заключаем, что произведение их достигает наибольшей величины тогда, когда множители станут равны, т. е. когда осуществится равенство
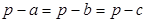
откуда 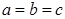
Итак, треугольник имеет при данном периметре наибольшую площадь тогда, когда стороны его равны между собой.
Глава 2. Методические особенности изучения площадей многоугольников в математических классах
2.1 Тематическое планирование и особенности преподавания в классах с углубленным изучением математики
| № | Содержание изучаемого материала | Кол-во часов |
| Площади многоугольников. | 26 | |
| 1 | Вычисление площадей в древности. | 1 |
| 2 | Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника». | |
| Понятие о площади. Свойства площади. | 1 | |
| Понятие о многоугольнике. | 1 | |
| Понятие о площади многоугольника. Дескриптивное определение. | 1 | |
| 3 | Различные формулы площадей многоугольников. | 1 |
| 4 | Вывод формул площадей многоугольников | |
| Площадь треугольника. Формула Герона. | 2 | |
| Площадь прямоугольника. | 1 | |
| Площадь трапеции. | 1 | |
| Площадь четырёхугольника. | 2 | |
| Универсальная формула. | 1 | |
| Площадь n -угольника. | 3 | |
| Вычисление площади многоугольника по координатам его вершин. | 2 | |
| Формула Пика. | 3 | |
| 5 | Теорема Пифагора. | 2 |
| 6 | Равносоставленность многоугольников. Теорема Больяя-Гервина. | 1 |
| 7 | Отношение площадей подобных многоугольников | 1 |
| 8 | Фигуры с наибольшей площадью | 2 |
В углубленном изучении математики выделяются два этапа, отвечающие возрастным возможностям и потребностям и потребностям школьников и соответственно различающимся по целям.
Первый этап углубленного изучения математики является в значительной мере ориентационным. На этом этапе ученику надо помочь осознать степень своего интереса к предмету и оценить возможности овладения им, с тем, чтобы по окончании IX класса он смог сделать сознательный выбор в пользу дальнейшего углубленного выбор в пользу дальнейшего углубленного либо обычного изучения математики. Интерес и склонность учащегося к математике должны всемерно подкрепляться и развиваться. В случае же потери интереса, изменения его в другом направлении ученику должна быть обеспечена возможность перейти от углубленного изучения к обычному.
Углубленное изучение на втором этапе предполагает наличие у учащихся более или менее устойчивого интереса к математике и намерение выбрать после окончания школы связанную с ней профессию. Обучение на этом этапе должно подготовить подготовку к поступлению в вуз и продолжению образования, а также к профессиональной деятельности, требующей достаточно высокой математической культуры.
При углубленном изучении математики учащиеся должны приобрести умения решать задачи более высокой по сравнению с обязательным уровнем сложности, точно и грамотно формулировать изученные теоретические положения и излагать доказательства теорем, правильно пользоваться математической терминологией и символикой.
Следует иметь в виду, что требования к знаниям и умениям учащихся при углубленном изучении математики не должны быть завышены. Чрезмерность требований порождает перегрузку, что ведёт, особенно на первом этапе, к угасанию интереса к математике. Поэтому требования к результатам углубленного изучения математики на первом этапе ненамного превышает требования общеобразовательной программы. Требования на втором этапе в соответствии с его целями согласуются со средним уровнем требований, предъявляемых вузами к математической подготовке абитуриентов. Заметим, что минимальный обязательный уровень подготовки, достижение которого учащимися является необходимым и достаточным условием выставления ему положительной оценки, при углубленном и обычном изучении математики один и тот же. Однако тем учащимся классов с углубленным изучением математики, успехи которых в течении длительного времени не поднимаются выше минимального обязательного уровня.
Успешность решения задач углубленного изучения математики во многом зависит от организации учебного процесса. Учителю предоставляется возможность свободного выбора методических путей и организационных форм обучения, проявления творческой инициативы. Однако при этом следует иметь в виду ряд общих положений, изложенных ниже.
— Учебно-воспитательный процесс должен строится с учётом возрастных возможностей и потребностей учащихся.
— Основной причиной отсева школьников из классов с углубленным изучением математики является перегрузка, поэтому не следует стремиться к чрезмерному насыщению программы дополнительными вопросами.
— Углубленное изучение математики предполагает прежде всего наполнение курса разнообразными, интересными и сложными задачами, овладение основным программным материалом на более высоком уровне.
— Для поддержания и развития интереса к предмету следует включать в процесс обучения занимательные задачи, сведения из истории математики. Это особенно важно на первом этапе, когда интерес учащихся ещё недостаточно устойчив.
— На втором этапе возрастает роль теоретических знаний, становятся весьма значимыми такие их качества, как системность и обобщённость. Значительное место должно быть уделено решению задач, отвечающих требованиям для поступающих в вузы, где математика является профилирующим предметом.
— В связи с тем, что в классы с углубленным изучением приходят школьники с разным уровнем подготовки, в процесс обучения на каждом этапе должны быть включены повторение и систематизация опорных знаний.
— Учебный процесс должен быть ориентирован на усвоение учащимися прежде всего основного материала; при проведении текущего и итогового контроля знаний качество усвоения этого материала проверяется в обязательном порядке.
— Значительное место в учебном процессе должно быть отведено самостоятельной математической деятельности учащихся – решению задач, проработке теоретического материала, подготовке докладов, рефератов и т. д.
— Очень важно организовать дифференцированный подход к учащимся, позволяющий избежать перегрузки и способствующий реализации возможностей каждого из них.
2.2 Методика проведения уроков
Тема: «Решение задач с использованием свойств площадей»
Цель : Освоение различных путей поиска решения задач с использованием свойств площадей.
Оборудование : Таблица «Свойства площадей».
Сегодня мы на уроке будем решать задачи с использованием свойств площадей.
Двух учеников приглашают к доске.
I. Запишите на доске все формулы площади треугольника.
II. Запишите на доске формулы площади трапеции.
I. 1).
2)
3) 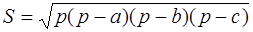
где
4)
5) 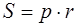
r – радиус вписанной в треугольник окружности
6)
II. 1).
2) 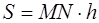
3) 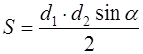
где d 1 , d 2 – диагонали трапеции, α – угол между ними
4) 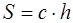
где с – боковая сторона трапеции, h –перпендикуляр из середины другой боковой стороны на первую или её продолжение
Пока ученики записывают формулы, спросить учеников с мест правила «Свойства площадей».
1). Каждая фигура имеет положительную площадь.
2). Площадь квадрата со стороной равной единице длины равна единице площади.
3). Если фигура разбивается на две части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.
Рассмотрите площади треугольника, написанные на доске.
Вопрос . Какая из формул является основной?
Ответ . 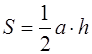
Назовите следствия из этой формулы, используя таблицу «Свойства площадей».
С–1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не изменится.
С–2. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
С–3. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
С–4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
С–5. Медиана треугольника делит его на 2 равновеликие части.
С–6. Медианы треугольника делят его на три равновеликие части.
С–7. Медианы треугольника делят его на 6 равновеликих частей.
С–8. Средняя линия треугольника площади 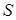
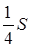
Задача 1 . Дано 
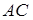
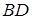
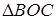
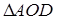
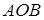
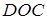
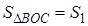
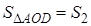
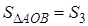
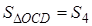
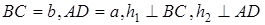
Найдите связь между площадями треугольника.
Выразите площадь трапеции через 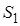
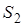
Так как 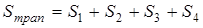
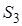
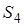
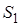
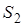
Вопрос . Что можно сказать про площади 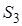
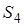
Ответ . 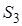
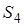
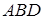
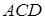
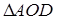
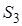
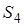
Выразите 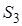
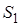
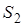
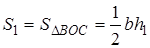
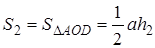
Докажите, что 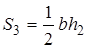
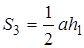
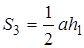
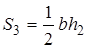
Перемножив (2.1) и (2.2), получим
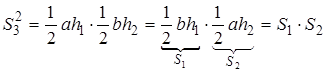
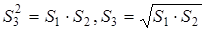
Вопрос . Как сформулировать правило, которое мы вывели?
Ответ . Площадь треугольника, прилегающего к боковой стороне трапеции есть среднее геометрическое между площадями треугольников, прилегающих к основаниям трапеции.
Вопрос . Как вывести соотношение 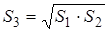
Ответ . 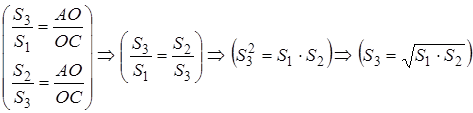
Вопрос . Какое свойство площадей здесь использовались?
Ответ . С – 3, С – 2 (ученики отвечают устно).
Вопрос . Как можно ещё вывести соотношения 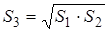
Ответ . 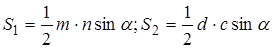
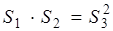
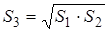
Найдите площадь трапеции (рис. 2.3)
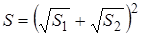
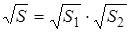
Таким соотношением связана площадь трапеции с площадями треугольников, прилегающих к её основаниям. Итак, для трапеции
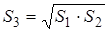
Вопрос . Справедливо ли это соотношение для любого четырёхугольника?
Ответ . Нет, т. к. 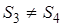
Основания у треугольников 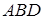
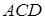
Вопрос . А какое соотношение между 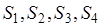
Ответ . 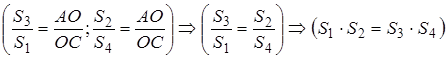
т. е. произведения площадей треугольников, прилегающих к противоположным сторонам четырёхугольника равны.
Задача 2 . (обратная).
Дано : выпуклый четырёхугольник
Докажите, что этот четырёхугольник есть трапеция.
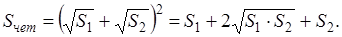
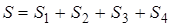
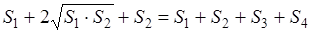
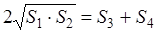
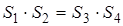
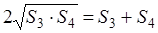
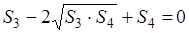
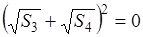
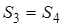
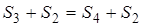
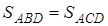
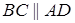
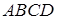
Задача 3 . Через некоторую точку, взятую внутри треугольника проведены 3 прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют треугольник на 6 частей, из которых три треугольника с площадями 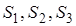
Дано : 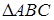
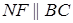
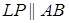
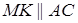
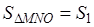
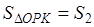
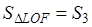
Найдите 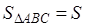
1)
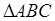
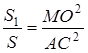
2) 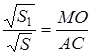
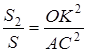
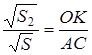
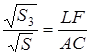
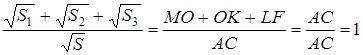
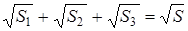
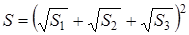
Повесить таблицу «Итог урока» (сделать из достаточно плотной бумаги, с магнитами на обратной стороне, прикрепляется мгновенно на обратную доску).
Вопрос . Мысленно вернитесь ко всем задачам, которые были рассмотрены на уроке. Попытайтесь вспомнить из всех свойств площадей, какие свойства мы применяли на уроке.
Ответ . 1) Равные фигуры имеют одинаковые площади.
2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.
3) Если от равных отнять равные, то получим равные.
Вопрос . Какие следствия из формулы 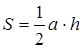
Ответ . С – 1, С – 2, С – 3, С – 4, С – 5 все следствия ученики рассказывают.
Вопрос . Из множества формул для нахождения площади простых фигур какие бы вы использовали?
Ответ . 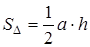
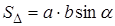
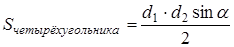
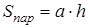
1. Диагонали делят трапецию на 4 треугольника. Площади двух из них равны 1 см 2 и 2 см 2 . Какой может быть площадь трапеции?
2. Точки 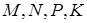
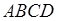
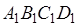
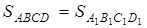
3. Дано: 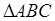
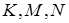
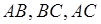
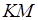
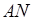
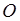
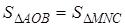
4. В параллелограмме 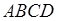
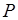
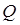
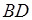
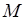
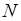
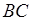
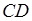
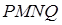
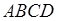
5. На одной стороне угла с вершиной 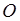
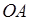
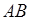
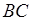

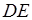
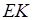
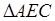
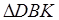
Домашнее задание выдаётся каждому ученику на листке.
Тема: «Понятие площади. Площадь квадрата»
Цели урока : 1) учащиеся должны понять практическую необходимость измерения площадей;
2) усвоить: свойства простой фигуры; формулу вычисления площади квадрата и уметь её доказывать с учётом того, каким числом измеряется длина стороны квадрата – рациональным или иррациональным.
Вспомните известные ранее единицы измерения площади (1 мм 2 , 1 см 2 , 1 дм 2 , 1 м 2 , 1 км 2 , 1 ар, 1 га), равносильность этих единиц:
1) 1 см 2 = 100 мм 2 ;
2) 1 дм 2 = 100 см 2 = 10 000 мм 2 ;
3) 1 м 2 = 100 дм 2 = 10 000 см 2 = 1 000 000 мм 2 ;
4) 1 ар = 100 м 2 ;
5) 1 га = 100 ар = 10 000 м 2 ;
6) 1 км 2 = 100 га;
7) 1 см 2 = 0, 01 дм 2 ;
8) 1 м 2 = 0, 000001 км 2 ;
9) 1 дм 2 = 0, 01 м 2 ;
10) 1 ар = 0, 01 га;
11) 1 м 2 = 0, 01 ар = 0, 0001 га.
2. Проверка задания на дом
Опрос по домашнему заданию, которое заключалось в следующем: узнайте из литературы, как появилась необходимость измерения площадей в древности в различных странах (Египте, Китае, Индии, России и др.); приведите примеры необходимости вычисления площадей в настоящее время.
1-й ученик . Геометрия возникла ещё в глубокой древности в связи с практическими потребностями человека. Измерения расстояний, изготовление орудий труда определённых размеров, нахождение площади земельного участка, вместимость сосудов и т. д. Слово геометрия – греческого происхождения ( гео – земля, метрио – меряю) и означает землемерие .
2-й ученик . Ещё 4-5 тыс. лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Для вычисления площади произвольного четырёхугольника древние египтяне четыре тысячи лет назад использовали формулу
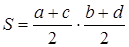
где 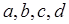
3-й ученик . Практический характер имела и древнеиндийская геометрия, развитие которой связано как с повседневными жизненными потребностями, так и с религиозными обрядами, с культом жертвоприношения. В труде «Сульва-Сутра» встечаются вопросы вычисления площадей, деления площадей прямоугольников, квадратов и трапеций с помощью прямых.
4-й ученик . В произведении «Патиганита» — руководству по арифметике и измерению фигур – предложена формула:
где 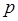
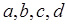
5-й ученик . В древней Руси уже в XVI в. нужды землемерия, строительства, военного дела привели к созданию сочинений по геометрии. Первое дошедшее до нас сочинение такого рода, называется «О земном верстании», написано при Иване IV в 1556 г. В этой рукописи все геометрические сведения сводятся к вычислению площадей квадрата, прямоугольника, треугольника и равнобочной трапеции.
6-й ученик . Практическая необходимость измерения площадей возникает в быту и на производстве и в настоящее время. Так, например, площадь зеркала водохранилища нужно знать проектировщикам, чтобы определить, как будет испаряться вода из заполненного водохранилища.
7-й ученик . Площадь поверхности стен помещения нужно знать строителям до того, чтобы рассчитать необходимое для их покрытия количество краски, обоев и кафеля.
8-й ученик . Площадь поверхности дороги нужно знать при расчёте необходимого для её покрытия количества асфальта.
3. Объяснение нового материала
Будем рассматривать площадь многоугольника. Можно сказать, что площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.
1 см 2 – площадь квадрата со стороной 1 см;
1 м 2 – площадь квадрата со стороной 1 м и т. д.
Площадь многоугольника – это положительное число, которое показывает, сколько раз единица измерения и её части укладываются в данном многоугольнике.
На плакатах рисунки
Нецелые квадраты со стороной 1 см можно разбить на квадраты с ещё меньшей длиной стороны. Любой многоугольник можно разбить на квадраты и треугольники. Но такой способ измерения площадей неудобен. Существуют формулы для вычисления площадей, которые учитывают следующие свойства площадей.
1. Равные многоугольники имеют равные площади.
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
3. Площадь квадрата равна квадрату его стороны.
Докажем третье свойство.
Случай 1 . Длина стороны квадрата выражается целым числом 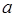
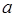
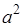
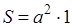
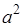
Случай 2 . Длина стороны выражается дробным числом
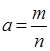
где 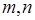
Примем 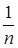
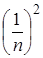
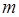
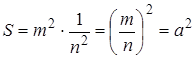
Случай 3 . Дина стороны квадрата выражается иррациональным числом или бесконечной десятичной непереодической дробью, 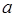
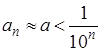
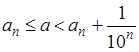
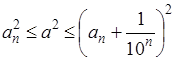
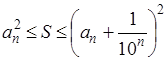
(На доске плакат с рисунком и выводом формулы.)
Будем неограниченно увеличивать число 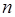
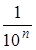
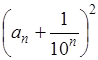
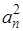
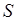
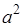
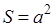
4. Решение задач
(Условия задач заранее написаны на доске.)
1 . (Устно.) вычислите площадь сечения дорожной трубы, изображённой на рисунке.
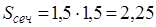
2 . Железная проволока, сечение которой 1 мм 2 , разрывается под действием груза в 40 кг. Какой нагрузкой разорвётся железный стержень, поперечное сечение которого – квадрат со стороной 24 мм.
Решение . 1. Найдём площадь поперечного сечения:
24 24 = 576 (мм 2 ).
2. Найдём массу груза, от которого разорвётся стержень:
576 40 = 23 040 (кг).
3 . Стороны двух участков земли квадратной формы соответственно равны 120 м и 50 м. Определите сторону квадратного участка земли, равновеликого двум участкам.
1) 120 2 = 14 400 (м 2 ) – площадь первого участка.
2) 50 2 = 2500 (м 2 ) – площадь второго участка.
3) 14 400 + 2500 = 16 900 (м 2 ) – площадь двух участков.
4) 16 900 = 130 2 – 130 – сторона квадратного участка, равновеликого первым двум участкам.
4 . Площадь квадратного участка земли (масштаб 1: 10 000) равна
552, 25 м 2 . Найдите площадь участка в натуре.
552, 25 × 10 000 = 5 522 500 (см 2 ) = 552, 25 (м 2 ) – площадь участка в натуре.
5. Задание на дом
1. Определите площадь квадрата по его диагонали 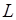
2. Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза? В 1,5 раза?
1 . Само возникновение геометрии говорит о практической направленности этой науки.
2 . Площадь квадрата выражается формулой 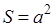
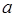
3 . Понятие площади является основополагающим не только в математике, но и в окружающем нас мире.
Тема: «Измерение площади фигуры с помощью палетки»
Цели: Научить выполнять приближённое вычисление площадей; познакомить с вычислением площади с помощью палетки по алгоритму; повторить единицы длины и единицы измерения площади; развивать мышление, внимание и память.
Оборудование . Учебник «Математика» (4-й класс, часть 1, авт. М. И. Моро и др.), таблица алгоритма, палетки, индивидуальные карточки, экран, эпидиаскоп, плёнки с фигурами.
I. Организационный момент
II. Сообщение темы урока
Учитель . Сегодня на уроке вы научитесь выполнять приближённое вычисление площади и познакомитесь с приспособлением для этого.
I. Знакомство с новым материалом
У. Рассмотрите фигуру на экране.
— Сколько места занимает фигура 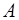
Выслушиваются ответы детей.
— Ответ на этот вопрос мы можем дать лишь приблизительно, указав границы, в которых находится площадь фигуры 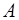
— Как мы будем рассуждать, чтобы вычислить площадь данной фигуры? Внутри фигуры 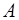
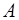
6 + 10 : 2 = 6 + 5 = 11 ед.
— Значит площадь нашей фигуры приблизительно 11 квадратных единиц.
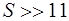
Всё это мы смогли вычислить благодаря тому, что фигура 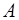
Дети . Самим расчертить фигуру на квадраты.
У. Правильно, но на это уйдёт много времени. Чтобы ускорить работу, люди придумали приспособление для определения площади фигур.
Учитель раздаёт детям прозрачные палетки, расчерченные на квадратные сантиметры и карточки с фигурами.
— Перед вами такое приспособление. Откройте учебники на странице 49 и прочитайте, как оно называется.
Д. Для приблизительного определения площади фигуры используется палетка.
Палетка – прозрачная плёнка, разделённая на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры.
У. Посмотрите на ваши палетки. Как они разделены?
Д. На квадратные сантиметры.
У. В учебнике на странице 49 на цветные фигуры также наложена палетка, разделённая на квадратные сантиметры. Прочитайте, как находили площадь фигуры голубого цвета.
Дети читают текст, отмеченный красной чертой.
— Чему равна площадь этой фигуры?
Д. Примерно 31 квадратный сантиметр.
У. Попробуем вывести формулу, по которой приблизительно считается площадь.
Дети вместе с учителем выводят и записывают формулу.
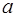
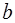
— Найдите площадь фигур зелёного и розового цветов.
Д. Площадь зелёной фигуры приблизительно равна 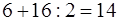
— Площадь розовой фигуры приблизительно равна 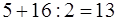
У. Возьмите в руки карточки с изображёнными на них фигурами. С помощью палетки найдите их площадь.
Дети выполняют задание.
— Попробуем вывести алгоритм нахождения площади фигуры при помощи палетки.
Учитель записывает каждый шаг на доске.
1. Наложить палетку на фигуру.
2. Сосчитать число 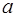
3. Сосчитать число 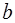
4. Сосчитать приближенное значение площади.
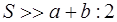
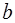
V. Практическая работа
У. Нарисуйте на листе бумаги какую-нибудь замкнутую линию и найдите площадь фигуры, ограниченной этой линией.
Дети выполняют задание в тетради, находят площадь, называют свои ответы.
— Начертите циркулем окружность радиусом 4 сантиметра, найдите с помощью палетки площадь получившегося круга.
Дети находят площадь.
VI. Закрепление пройденного материала
У. Найдите задание 265 на странице 50. Задание выполняем по вариантам: вариант 1 – первая часть номера, вариант 2 – вторая часть.
Дети самостоятельно выполняют задание.
— Поменяйтесь тетрадями и проверьте работу ваших соседей.
Дети делают проверку.
— Вычислите периметр и площадь многоугольника.
Ученики выполняют задание по вариантам: вариант 1 – находят периметр, вариант 2 – находят площадь.
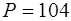
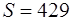
— Решите логическую задачу. Для каждой фигуры объясните, почему она лишняя.
Д. сначала уберём фигуру 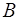
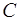
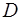
VII. Самостоятельная работа
У. Выполните упражнения 267 и 262.
Дети выполняют работу и сдают тетради.
VIII. Итог урока
У. С помощью какого инструмента вы научились находить приближённое значение площади фигуры?
Д. С помощью палетки.
У. Какой формулой вы пользовались?
Д. 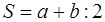
У. Кто из вас научился выполнять приближённое вычисление площади фигуры?
Дети поднимают руки.
IX. Домашнее задание
Учитель раздаёт карточки с цифрой 5.
У. Дома вычислите площадь цифры и решите задачи 261 и 263.
Тема: «Площадь прямоугольного треугольника»
Цели урока : 1) научить находить площадь прямоугольного треугольника; применять формулу для решения практических задач;
2) развивать познавательный интерес учащихся;
3) воспитывать ответственность за достигнутый результат.
Класс делится на четыре группы. Для работы на уроке каждой группе необходимы:
а) цветные жетоны для «светофора» («светофор» — это сигнал обратной связи, в конце урока ученики с его помощью сигнализируют учителю: красный – ничего не понял; жёлтый – понял, но не очень хорошо; зелёный – всё хорошо понял);
б) две большие одинаковые модели прямоугольного треугольника;
в) карточки с изображениями прямоугольных треугольников для самостоятельной работы;
г) конверт с деталями для практической работы;
д) доски и пластилин.
Тема: «Площадь прямоугольного треугольника»
а) 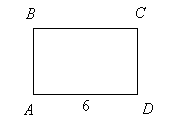
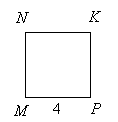
| А | Н | У | Е | Р | Т |
| 9 | 12 | 6 | 20 | 10 | 18 |
Жили-были два брата:
треугольник с квадратом.
Стал расспрашивать квадрат:
«Почему ты злишься брат?»
Тот кричит ему: «Смотри,
Ты полней меня и шире.
У меня улов лишь три,
У тебя их все четыре».
Но квадрат ответил: «Брат!
Я же старше, я – квадрат».
И сказал ещё нежней:
«Незвестно, кто нужней!»
2. Постановка вопроса : так кто же нужней, кто важней?
Вспомним, что мы знаем о квадрате, прямоугольнике и прямоугольном треугольнике.
3. Опрос в форме викторины.
За правильный ответ группа получает жетон.
1. Какой четырёхугольник называется прямоугольником?
2. Какой четырёхугольник называется квадратом?
3. Какой треугольник называется прямоугольным?
4. Как называется сторона прямоугольника?
5. Как называются стороны прямоугольного треугольника?
6. Назовите катеты и гипотенузу прямоугольного треугольника, изображённого на доске?
7. Как называется отрезок, соединяющий противолежащие вершины прямоугольника?
8. Как быстро вырезать два равных прямоугольных треугольника?
9. Как найти площадь прямоугольника, квадрата?
10. Найдите площадь прямоугольника, квадрата, изображённых на доске.
11. Знаете ли вы, как найти площадь прямоугольного треугольника?
4. Нахождение площади прямоугольного треугольника .
Перед учениками модели двух равных прямоугольных треугольников. Как найти площадь каждого из них? (Ученики догадываются, что нужно площадь прямоугольника разделить пополам.)
Площадь прямоугольного треугольника равна половине произведения катетов: 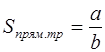
6. Проверяем, как ученики поняли эту формулу ?
а) Найдите площадь 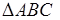
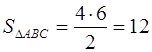
б) Найдите площадь моделей, выполнив необходимые измерения:
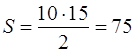
в) найдите площади прямоугольных треугольников, изображённых на карточках.
Для этого нужно измерить катеты, найти их произведение и разделить его на 2.
Найдите площадь треугольника
7. Отвечаем на вопрос : Зачем нужно уметь находить площади фигур, в частности, площадь прямоугольного треугольника? (В строительстве, швейном деле и т. д.)
8. Ролевая игра . Известный художник Половинкин прославился своими работами-мозаиками.
Придумайте свой узор. С помощью пластилина на досках из различных деталей ребята составляют свою мозаику (работа в группах).
Узнайте, сколько «материала» потребуется для мозаики. Для этого найдите площади треугольников, из которых состоит мозаика.
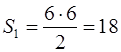
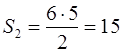
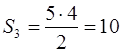
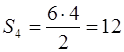
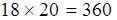
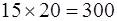
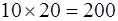
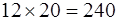
9. а) Как же разрешить спор между квадратом и треугольником?
б) Подведение итогов. Награждение команд и отличившихся учеников вымпелами.
в) Ответный сигнал «Светофор».
2.3 Результаты опытно-экспериментальной работы
С целью практического обоснования выводов, полученных в ходе наблюдения за деятельностью учащихся двух восьмых классов нами был проведён частичный психолого-педагогический эксперимент в средней общеобразовательной школе № 10 с. Бурлацкого Благодарненского района Ставропольского края.
Работа предусматривала несколько этапов. На первом этапе проводился констатирующий эксперимент, направленный на выяснение уровня сформированности методов научного познания у учащихся восьмых классов.
На следующем этапе была проведена сери экспериментальных занятий, направленных на формирование у учащихся основ методов научного познания.
Заключительный этап исследования проводился теми же методами, что и первый. Затем следовало подведение итогов опытно-экспериментальной работы. Рассмотрим подробнее каждый из этапов.
1. Констатирующий этап эксперимента
Опытно-экспериментальная работа велась в двух восьмых классах средней общеобразовательной школы № 10 с. Бурлацкого Благодарненского района Ставропольского края. В экспериментальном классе участвовало 20 человек, а в контрольном – 18 человек, таким образом, участвовало 38 человек. В рамках данного этапа были использованы следующие методы:
1. Невключённые наблюдения;
3. Метод математической и статистической обработки данных.
На данном этапе эксперимента нами были апробированы задания. Цель их состояла в выявлении уровня общей сформированности методов решения геометрических задач. На этом этапе принимало участие два восьмых класса, каждому из которых были предложены задания, содержащие приёмы: классификация, аналогия, анализ, обобщение.
1. Дан равнобедренный треугольник 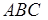
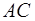
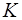
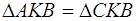
2. В треугольнике 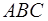
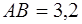
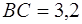
3. Начертите фигуру так, чтобы её можно было разбить на 2 равных треугольника.
4. Дан параллелограмм. Проведите два отрезка так, чтобы получилось четыре пары равных треугольников.
5. Известно, что в параллелограмме 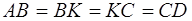
Проанализировав работы, мы получили следующие результаты:
Результаты выполнения работы в экспериментальном классе
| Полностью верно | Частично верно | Не верно | Не приступили к выполнению задания | ||||
| чел. | % | чел. | % | чел. | % | чел. | % |
| 6 | 30 | 3 | 15 | 9 | 45 | 2 | 10 |
Результаты выполнения заданий в контрольном классе
| Полностью верно | Частично верно | Не верно | Не приступили к выполнению задания | ||||
| чел. | % | чел. | % | чел. | % | чел. | % |
| 5 | 28 | 6 | 29 | 5 | 28 | 2 | 15 |
Как видно из таблиц на данном этапе работы нет существенных отличий экспериментального класса и контрольного. По полученным данным можно судить, что сформированность методов решения геометрических задач находится на уровне ближе к среднему.
Анализ детских работ также показал, что наиболее сложными оказались задания №1 и №5. Остальные задания не вызвали особых затруднений.
2. Поисковый этап исследования
На данном этапе мы изучали тему теоретически и подбирали задания для работы с учащимися для получения результатов исследования.
С этой целью были проанализированы более 15 источников научной литературы по проблеме исследования, отобраны, систематизированы и дополнены задания, упражнения, игры, которые бы помогли освоить методы решения геометрических задач учащимися средней школы. Также на данном этапе эти задания проходили частичную апробацию для отбора наиболее эффективных.
3. Нормирующий этап эксперимента
Эксперимент длился с января по март 2004 года. В течение этого времени экспериментальный класс в ходе учебно-воспитательного процесса получал дополнительные задания на уроках математики на овладение методами решения геометрических задач.
Цель этого этапа заключалась в проверке эффективности подобранной системы заданий в реальной практике.
На данном этапе использовались такие методы, как и на констатирующем, то есть:
1. Невключённое наблюдение;
3. Метод математической и статистической обработки данных.
Второй срез был проведён в начале формирующего этапа эксперимента. Участникам были предложены задания, которые были видоизменены и дополнены по сравнению с 1 срезом.
1. В некотором четырёхугольнике диагонали равны, а он не прямоугольник, диагонали взаимно перпендикулярны, а он не ромб. Что это за фигура?
2. На взаимно перпендикулярных прямых 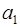
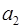
3. В некотором четырёхугольнике известен один из углов. Какого вида может быть этот четырёхугольник, чтобы было возможно вычислить все остальные углы этого четырёхугольника?
4. Дан равносторонний треугольник. Что нужно знать, чтобы вычислить его сторону?
Проанализировав выполнение работы, мы получили следующие результаты.
Таблица 3. Результаты выполнения работ в экспериментальном классе
| Полностью верно | Частично верно | Не верно | Не приступили к выполнению задания | ||||
| чел. | % | чел. | % | чел. | % | чел. | % |
| 7 | 35 | 12 | 60 | 1 | 5 | 0 | 0 |
Таблица 2.Результаты выполнения заданий в контрольном классе
| Полностью верно | Частично верно | Не верно | Не приступили к выполнению задания | ||||
| чел. | % | чел. | % | чел. | % | чел. | % |
| 6 | 33 | 11 | 61 | 1 | 6 | 0 | 0 |
По данным таблиц 3 и 4 можно сделать вывод, что результаты проведённого II тестирования незначительно отличаются от I. Дети достаточно владеют методами решения геометрических задач, с охотой принимаются за выполнение заданий. Нужно отметить, что предложенные задания не вызвали затруднений у учащихся обоих классов, т. к. ни в экспериментальном, ни в контрольном классах не было учащихся, которые не приступили к выполнению предложенных заданий. Третий срез был проведён в конце формирующего этапа эксперимента. Целью этого среза было выявление уровня эффективности проводимой опытно-экспериментальной работы по развитию логического мышления школьников на основе овладения ими методов решения геометрических задач. Предложенные задания для 3 среза были повышенной трудности по сравнению с 1 и 2 срезами. 1. Какую часть площадь заштрихованной фигуры
составляет от площади треугольника (рис. 2.7)
2. что больше: площадь одного правильного треугольника со стороной 10 см или сумма площадей десяти правильных треугольников со стороной 1 см? После анализа детских работ нами были получены следующие показатели, которые внесены в таблицу 5.
Сравнительная таблица полученных результатов в экспериментальном и контрольном классах
| Полностью верно | Частично верно | Не верно | Не приступили к выполнению задания | |
| Экс., % | 85 | 15 | 0 | 0 |
| Контр.,% | 44 | 30 | 22 | 0 |
Из таблицы видно, что в экспериментальном классе значительно больше учащихся полностью верно выполняют предложенные задания, нет учащихся, которые бы вообще не приступили к выполнению. Результаты каждого класса позволяют сделать вывод, что уровень сформированности методов решения геометрических задач увеличился в рамках собственного класса.
Таким образом, в данной главе мы исследовали на теоретическом и практическом уровнях возможности применения различных заданий на приёмы умственных действий. Нами были разработаны системы заданий на приёмы мыслительных действий.
В главе освещён вопрос о таких методах как анализ и синтез. Эти методы нами рассмотрены вместе, так как в чистом виде анализ и синтез практически не встречаются. В частности, выясним, что ведущим звеном всякой мыслительной деятельности является анализ через синтез. Это основной нерв процесса мышления. Способность к аналитико-синтетической деятельности находит своё выражение не только в умении выделять элементы того или иного объекта, его различные признаки или соединять элементы в единое целое, но и умении включать их в новые связи, увидеть их новые функции.
Также нами рассмотрен мыслительный приём обобщения, отмечена зависимость обобщения от анализа. Выделены особенности эмпирического и содержательного обобщения. В частности отметим, что результатом эмпирического обобщения являются житейские понятия в науке. А провести содержательное обобщение – значит, открыть некоторую закономерность, взаимосвязь особенных и единичных явлений с общей основой целого. Так как приём обобщения является достаточно сложным для детей школьного возраста, нами предложены дидактические задачи, используемы при обобщении знаний учащихся. Они способствуют лучшему усвоению материала и облегчают информационную нагрузку на мозг при обобщении.
Также в данной главе мы рассмотрели приём абстрагирования, который заключается в отвлечении от несущественных признаков и выведение на первый план существенных.
Полученные в результате опытно-экспериментальной работы данные позволили нам судить об эффективности применения мыслительных операций: анализа, синтеза, обобщения, сравнения и других в развитии логического мышления школьников. Несмотря на то, что сроки проведения психолого-педагогического эксперимента были ограничены, а исследуемая проблема требует более длительного изучения, как в теоретическом, так и в практическом отношении, мы смогли , мы смогли получить необходимые данные, подтверждающие гипотезу о том, что если в процессе изучения раздела геометрии обращать внимание на освоение методов решения геометрических задач, то это повысит эффективность обучения математике и будет способствовать развитию логического мышления учащихся.
Заключение
Результаты исследования по теме квалификационной работы, и проведённый эксперимент позволяют сделать следующие выводы:
1. Разработана методика занятий в математических классах по теме «Площади многоугольников».
2. В классах с углубленным изучением математики учащиеся познакомились с новыми для них формулами площадей многоугольников и выводами некоторых из них. Основная сложность изучения материалам состоит в том, что не существует единого универсального метода в нахождении площади n -угольника.
3. Особое внимание в работе уделено выводам формул площадей многоугольников, не рассматриваемых в школьном курсе математики.
4. Разработана система упражнений, способствующая сознательному усвоению учащимися предлагаемого материала по теме квалификационной работы.
5. Представленный в работе материал апробирован в средней общеобразовательной школе № 10 с. Бурлацкого Благодарненского района Ставропольского края на занятиях в 8-9 классах. Материал вполне доступен учащимся и вызывает у них должный интерес, лучше развивает их логическое мышление.
Таким образом, в результате проведённой работы видим, что целесообразно углубить в школьном курсе математики изучение темы «Площади многоугольников».
Литература
1. Александров А. Д., Вернер А. Л., Рыжик В. И. Геометрия 7-9. Учебник для общеобразовательных учреждений.- М.: Просвещение, 1995.
2. Александров А. Д., Вернер А. Л., Рыжик В. И. Геометрия 8/9. Учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1996.
3. Атанасян Л. С., Базылев В. Т. Геометрия. Для студентов педагогических институтов. – М.: Просвещение, 1987.
4. Атанасян Л. С. Геометрия 7-9. учебник для общеобразовательных учреждений.- М.: Просвещение, 2000.
5. Бевз Г. П., Бевз В. Г., Владимирова Н. Г. Геометрия 7-11. Учебник для общеобразовательных учреждений.- М.: Просвещение, 1996.
6. Березина Л. Ю., Мельникова И. Б. Геометрия в 7-9 классах – М., 1990.
7. Блок А. Я. Методика преподавания в школе. – М.: Просвещение, 1987.
8. Воропаева Р. Н. Методические советы из опыта преподавания//Математика, 2001, №35, с. 25-28.
9. Гильберт Д. Основания геометрии. – М. – Л.: Гостехиздат, 1948.
10. Глейзер Г. И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1964.
11. Еникеева О. Б., Крупич В. И. Учить школьников учиться математике. – М., 1990.
12. Ефимова А. И. Проблемы преподавания математики в школе. – С. – П., 1984.
13. Киселев А. И., Рыбкин Н. А. Геометрия: Планиметрия: 7-9 кл.:Учебник и задачник. – М.: Дрофа, 1995.
14. Колмогоров А. Н. Математика в её историческом развитии. – М.: Наука, 1991.
15. Корешкова Т. А., Цукерман В. В. Многоугольники и их площадь в шеольном курсе математики// Математика в школе, 2003, №9, с. 10-18.
16. Макарова Н. Д. Площадь. Единицы площади// Математика, 2002, №10, с. 30-31.
17. Математический энциклопедический словарь. – М. «Советская энциклопедия», 1988.
18. Перельман Я. И. Занимательная геометрия. Гос-ное изд-во технико-теоретической литературы. Москва – 1950. Ленинград.
19. Погорелов А. В. Геометрия 7-11. Учебник для общеобразовательных учреждений. – М.: Просвещение, 1999.
20. Прицнер Б. С. Площадь четырёхугольника// Математика в школе, 1989, №5, с. 21-22.
21. Рохлин В. А. Площади и объём. Энциклопедия элементарной математики. – М.: Наука, 1966.
22. Рыбников К. А. История математики. – М.: МГУ, 1994.
23. Сефибеков С. Р. Внеклассная работа по математике: кн. Для учителя. – М.: Просвещение, 1988.
24. Шевченко И. Н. Методы обучения математике // Минск. Высшая школа, 1977.
25. Энциклопедический словарь юного математика для старшего и среднего школьного возраста. – М.: Педагогика, 1989.
26. Юшкевич А. П. История математики. – М., 1970.





 ,
,














































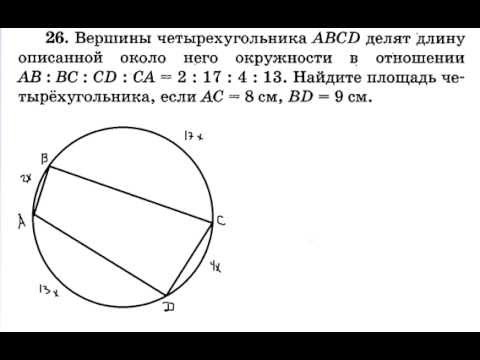





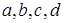 (рис. 1.1) применялась формула
(рис. 1.1) применялась формула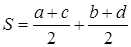 (1.1)
(1.1)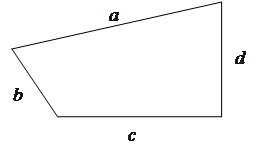

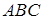 (рис. 1.2), в котором
(рис. 1.2), в котором 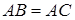 , египтяне пользовались приближенной формулой:
, египтяне пользовались приближенной формулой: