На основании свойств параллельных проекций кривых второго порядка можно утверждать, что в общем случае ортогональной проекцией окружности служит эллипс.
При проецировании окружности г на плоскость П’ (рис. 133) любая пара ее взаимно перпендикулярных диаметров проецируется в пару сопряженных диаметров эллипса /. Большая ось А’В’ эллипса / является проекцией такого диаметра окружности, который параллелен плоскости П’ и проецируется на нее без искажения. На рис. 133: АВ || П’ => А’В’ = АВ = 2R. Диаметр АВ расположен на линии уровня плоскости Т.
Остальные диаметры окружности проецируются отрезками меньшей длины. Наименьшим диаметром эллипса / служит его малая ось C’D’, которая является проекцией диаметра CD, перпендикулярного к диаметру АВ. Диаметр CD расположен на линии ската s плоскости Т. Угол ОБО’ между линией s и ее проекцией s’ является линейным углом двугранного угла а (а = П’, Л Т), поэтому C’D’=CD • cosa = 2R cosa.
Рассмотрим примеры построения на комплексном чертеже проекций окружности с центром О и радиусом R.
Пример 1 (рис. 134). Окружность г расположена в плоскости уровня Н (Н || Па).
В этом случае фронтальной проекцией окружности служит отрезок гг (длиной 2R), а горизонтальной проекцией является окружность п(п = г).
Пример 2 (рис. 135). Окружность г расположена в проецирующей плоскости Т; Т1 Пг.
Фронтальной проекцией окружности служит отрезок гг (гг с Тг), а горизонтальной проекцией является эллипс п.
Окружность г проецируется без искажения своего вида на дополнительную плоскость проекций Ш (Щ || Т) => Г4 = г.
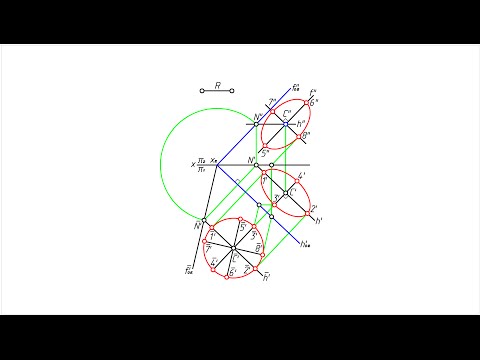
Пример 3 (рис. 136). Окружность г расположена в плоскости общего положения Т; Т = ; hnf = 0.
Окружность г проецируется на IIi и на Пг в виде эллипсов п и гг. Большая ось эллипса п расположена на линии hi и равна отрезку 11У—2г = 2R; большая ось эллипса гг расположена на линии /г и равна отрезку 132—42 = 2R.
Диаметры 11 —2| и |3—4 окружности г расположены соответственно на линиях уровня Ли/ плоскости Т. Малые оси эллипсов п и гг — отрезки 17у—5,| и 152—621 можно найти, используя проецирование окружности на дополнительные плоскости проекций Щ (П51П1; П51Т) и П4 (П4±П2; ЩЛТ).
Эту задачу можно решить, используя вращение окружности г вокруг линий уровня Л. Решите этот вариант самостоятельно.
Видео:ЗАДАЧИ НА НАКЛОННУЮ ПЛОСКОСТЬ - не ГРОБ! КАК ТАКИЕ РЕШАТЬ?Скачать

Проецирование окружности
Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.
Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.
Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к2, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л2. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п2 определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.
Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс4, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс4 описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л2. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.
Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.
Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.
Построение в плоскости общего положения а(Иа п /а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /га, и с радиусом, равным /?, начинают с определения проекций осей эллипса.
На горизонтальной проекции окружности по прямой /га‘ вправо и влево от точки О‘ откладывают радиус окружности Л, получая при этом точки А’ я В’. Сделав замену плоскостей проекций щ/л2 —> п/щ, где п4_1_ Иа, и построив новую проекцию окружности в виде отрезка С ,У /) |У , равного диаметру окружности, строят с помощью точек С’ и /)’ малую ось эллипса на горизонтальной проекции (направления построений указаны стрелками).
Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п5 Е/а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.
Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.
Видео:Задание 21 Проецирование окружностиСкачать

Построение проекций окружности
При выполнении чертежей деталей нередко возникает необходимость изображения окружностей, плоскости расположения которых не параллельны плоскостям проекций. Например, на рис. 7.13 окружность расположена в пространстве в плоскости β. В этом случае окружность проецируется в эллипс, а любая пара ее взаимно перпендикулярных диаметров проецируется парой сопряженных диаметров эллипса. Диаметр (1–2) окружности, параллельной плоскости проекций, проецируется без искажения и является для эллипса-проек-
ции большой осью (отрезок Iй2°). Остальные диаметры проецируются отрезками меньшей длины. Диаметр 3–4, перпендикулярный диаметру 1–2, проецируется как малая ось 3°4° эллипса: (1–2) 1 (3–4), (1–2) | π, следовательно, (3°4°) J.(I02°).
Пример построения горизонтальной проекции окружности, расположенной во фронтально проецирующей плоскости, приведен на рис. 7.14. Фронтальная проекция Г’0″2″ окружности совпадает с фронтальной проекцией а» фронтально проецирующей плоскости. Фронтальная проекция 3” ≡ 4″ диаметра окружности, перпендикулярного плоскости проекции π2, совпадает с фронтальной проекцией О « центра окружности. Горизонтальная проекция 3 ‘4’ этого диаметра, проецирующегося без искажения, является большой осью эллипса-проекции. Диаметр с фронтальной проекцией 7 «2» на горизонтальной проекции является малой осью 1 ‘2’ эллипса-проекции. На горизонтальной проекции показано построение одной из произвольных точек эллипса-проекции.
Пример построения проекций окружности, расположенной в плоскости общего положения, приведен на рис. 7.15. Плоскость задана проекциями А «О « и А ‘0’фронтали и В»О” и В’О’ горизонтали, пересекающимися в центре окружности с проекциями О «, О
🔥 Видео
Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Как начертить овал во фронтальной плоскостиСкачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Проекции окружности расположенной в плоскости общего положения. Метод вращенияСкачать
ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Изометрическая проекция окружности в плоскости ХУСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Урок 88. Движение по наклонной плоскости (ч.2)Скачать

2 3 проекция точки на конусеСкачать

Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Движение тела по наклонной плоскостиСкачать







