Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- Как рассчитать площадь четырехугольника
- Через диагонали и угол между ними
- Через стороны и противолежащие углы
- Площадь вписанного четырехугольника в окружность
- Площадь описанного четырехугольника около окружности через радиус
- Калькулятор расчета площади четырехугольника
- Расчет площади
- 1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 🎦 Видео
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат |  | S = a 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | ||
 | ||
 | ||
 | ||
| Параллелограмм | ||
 | ||
 | ||
 | ||
| Квадрат | ||
 | S = a 2 где | |
 | S = 4r 2 | |
 | ||
 | ||
| Ромб | ||
 | ||
 | ||
 | ||
 | ||
 | ||
| Трапеция | ||
 | ||
 | ||
 | ||
 | ||
| Дельтоид | ||
 | ||
 |  где | |
 | ||
 | ||
| Произвольный выпуклый четырёхугольник | ||
 | ||
| Вписанный четырёхугольник | ||
 | ||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
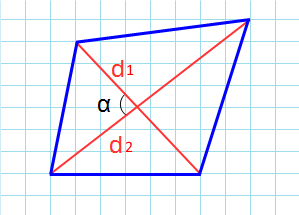
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
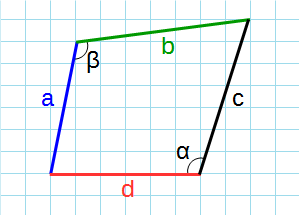
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
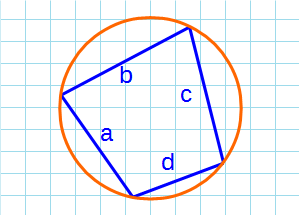
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
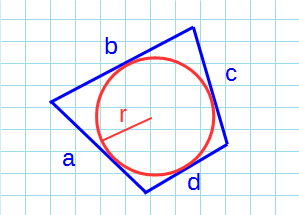
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Видео:✓ Площадь через диагонали | Ботай со мной #122 | Борис ТрушинСкачать

Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
🎦 Видео
Площадь четырёхугольника через диагоналиСкачать

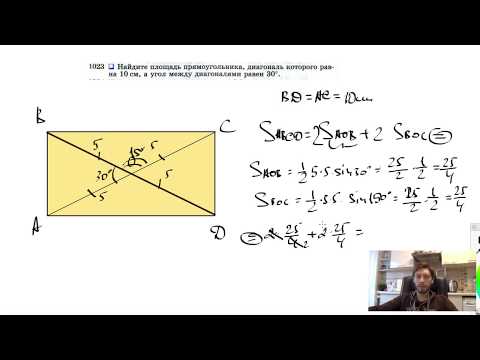
№1023. Найдите площадь прямоугольника, диагональ которого равна 10 см, а уголСкачать
Доказательство площади произвольного четырехугольника.Скачать

Все базовые формулы площади за 10 минут. Теперь ты их никогда не забудешьСкачать

Формула площадь четырехугольникаСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 6)Скачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

ОГЭ - 2023 И. В. Ященко. 50 вариантов. Вариант 12, задание 12. Найдите длину диагонали d первое.Скачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Четырехугольники. ПлощадиСкачать

Геометрия Как найти площадь четырехугольника, если нет формулыСкачать

Запомни: все формулы для площади треугольникаСкачать






 ,
,