Десятиугольник, вписанный в окружность
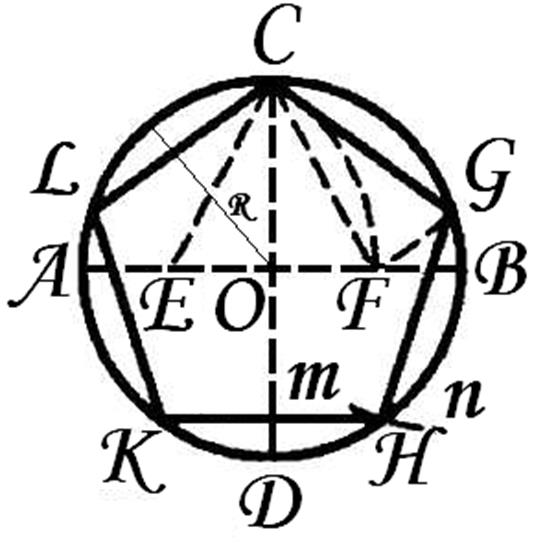
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.
Десятиугольник, описанный около окружности
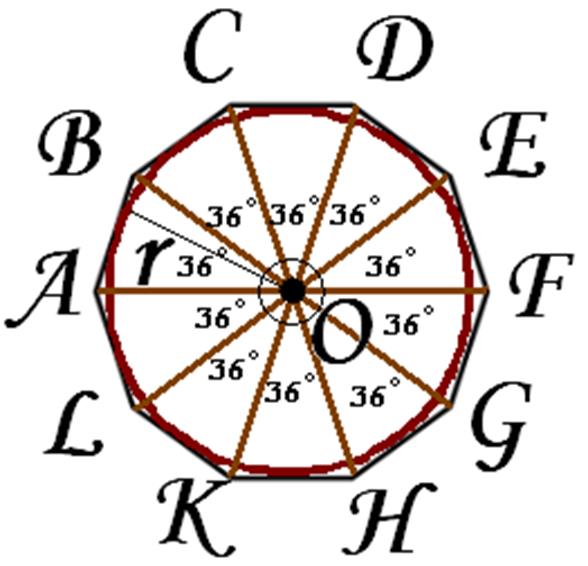
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
- Как начертить десятиугольник
- Как начертить угол без транспортира
- Как построить правильный восьмиугольник
- – циркуль;
- – линейка.
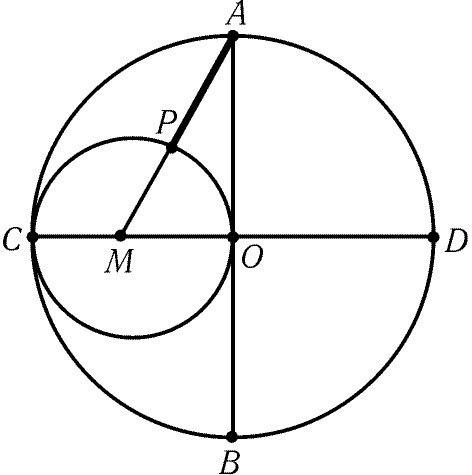
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.
Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.
| Правильный десятиугольник | |
|---|---|
 | |
| Сторон и вершин | 10 |
| Символ Шлефли | |
| Внутренний угол | 144° |
| Симметрия | Диэдрическая ( D 10 >  ), порядок 20. ), порядок 20. |
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
- Содержание
- Правильный десятиугольник [ править | править код ]
- Построение [ править | править код ]
- Разбиение правильного десятиугольника [ править | править код ]
- Пространственный десятиугольник [ править | править код ]
- Многоугольники Петри [ править | править код ]
- Объясни, как начертить десятиугольник. Составь план: с чего надо начать, что делать потом. Построй эту фигуру.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Построение правильного десятиугольника
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📺 Видео
Видео:Построение пятиугольника циркулемСкачать

Содержание
Видео:Построение пятиугольника циркулем и линейкойСкачать

Правильный десятиугольник [ править | править код ]
У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.
Площадь правильного десятиугольника равна (t — длина стороны):
A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>
Альтернативная формула A = 2.5 d t 
d = 2 t ( cos 3 π 10 + cos π 10 ) , >+cos >
ight),>
и может быть представлен в радикалах как
d = t 5 + 2 5 . >>>.>
Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> 

Радиус описанной окружности десятиугольника равен
R = 5 + 1 2 t , >+1> >t,>
а радиус вписанной окружности
r = 5 + 2 5 2 t . >>> >t.>
Построение [ править | править код ]
По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.
Иначе его можно построить следующим образом:
- Построить сначала правильный пятиугольник.
- Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
- Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.
Видео:Построение 10 угольника циркулемСкачать

Разбиение правильного десятиугольника [ править | править код ]
Гарольдом Коксетером было доказано, что правильный 2 m 


| Разбиение правильного десятиугольника |
|---|
Видео:Построение 12 угольника циркулемСкачать

Пространственный десятиугольник [ править | править код ]
| Правильные пространственные десятиугольники | ||
|---|---|---|
| # | # | # |
 | ||
Пентаграммная антипризма с перекрёстом
Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.
У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D5d [2 + ,10] симметрией порядка 20.
Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.
| Ортогональные проекции многогранников | |||
|---|---|---|---|
 Додекаэдр Додекаэдр | 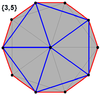 Икосаэдр Икосаэдр |  Икосододекаэдр Икосододекаэдр |  Ромботриаконтаэдр Ромботриаконтаэдр |
Многоугольники Петри [ править | править код ]
Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.
Видео:Геометрия - Построение десятиугольникаСкачать

Объясни, как начертить десятиугольник. Составь план: с чего надо начать, что делать потом. Построй эту фигуру.
Видео:Построение девятиугольника циркулем, приближенноеСкачать

Ваш ответ
Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать
![ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]](https://i.ytimg.com/vi/YKbgCquokWg/0.jpg)
решение вопроса
Видео:Деление окружности на 5 частей с помощью циркуляСкачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,036
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:4K Как построить десятиугольник, regular decagon constructionСкачать
Построение правильного десятиугольника
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Построение правильного
десятиугольника
Геометрия 9 класс
Правильные многоугольники
Авторы презентации: учителя информатики Приволжского района г.Казани -Талызина Л.К. ,Ларина А.У
Компьютерное тестирование
Задачи на построение
Построение правильного десятиугольника
Творческое задание на компьютере: «Математические человечки»;
Творческое домашнее задание
Используемая литература
Верно ли утверждение: если в многоугольнике все углы равны, то он правильный?
Найти число сторон правильного многоугольника, если его центральный угол равен 200.
Найти углы правильного десятиугольника.
Чему равна сумма внешних углов правильного n –угольника?
Пчелиные соты имеют форму многоугольника, сумма внутренних углов которого равна 7200.Найти число сторон этой соты.
Определить вид многоугольника., если каждая сторона его равна радиусу описанной окружности?
Найти отношение сторон правильного треугольника и шестиугольника, вписанных в окружность.
Вопросы компьютерного тестирования
Задачи на построение
Задача о построении циркулем и линейкой правильных многоугольников изучалась еще древнегреческими геометрами, а окончательно была решена лишь в 1801 году великим немецким математиком Карлом Гауссом.
На рисунке изображена лишь небольшая часть правильного многоугольника. Как узнать, сколько у него сторон? Закончить построение многоугольника.
2. Около правильного шестиугольника описана окружность. Предложить три способа нахождения центра этой окружности
Построение правильного десятиугольника
Алгоритм построения
1.Провести окружность O радиуса OA.
2.Из точки O1, как из центра, провести окружность, радиуса OO1.
3.Соединить точки A и O1.
4. Точку пересечения отрезка OA1 с окружностью обозначить B
5.AB- будет равен стороне искомого десятиугольника.
6.Из точки A , как из центра, провести окружность радиуса AB
7. Соединить точку пересечения окружности с точкой A
8.Полученный отрезок будет 1 стороной десятиугольника
и т.п.
Задание выполнено на компьютере в среде Free Hand
Математические человечки
Игра – шутка
Нарисовать на компьютере в среде Free Hand несколько человечков с помощью математических фигур. Затем подсчитать количество треугольников, квадратов, окружностей. По результатам можно определить какое качество преобладает в человеке: треугольник – ум, окружность – доброта, квадрат – интеллигентность. Затем можно выбрать самого умного, доброго, интеллигентного.
Творческое домашнее задание
Сделать паркет из правильных многоугольников
Используемая литература
Б. А. Кордемский. «Великие жизни в математике»
Н. Л. Вадченко «Проверьте свои знания»
С. Коваль «От развлечения к знаниям»
А. В. Погорелов «Геометрия. 7-11 классы»
Справочная литература
Дополнительная литература
Курс повышения квалификации
Охрана труда
- Сейчас обучается 99 человек из 45 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 350 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 219 человек из 53 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Деление окружности на равные части с помощью циркуляСкачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 532 222 материала в базе
Другие материалы
- 23.12.2020
- 104
- 0
- 23.11.2020
- 44
- 0
- 07.11.2020
- 49
- 0
- 07.10.2020
- 60
- 0
- 04.09.2020
- 58
- 0
- 28.08.2020
- 52
- 0
- 02.08.2020
- 63
- 0
- 01.08.2020
- 52
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 25.09.2020 321
- PPTX 1.1 мбайт
- 1 скачивание
- Оцените материал:
Настоящий материал опубликован пользователем Черных Лариса Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 20617
- Всего материалов: 200
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Курганской области школьников переведут на дистанционное обучение с 4 февраля
Время чтения: 1 минута
Рязанских школьников с 5 по 8 классы переведут на дистанционное обучение
Время чтения: 1 минута
Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Томске студентов вузов перевели на дистанционное обучение до конца февраля
Время чтения: 1 минута
Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📺 Видео
Построение 7 угольника циркулем, приближенноеСкачать

Построение 8 угольника циркулемСкачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

Построение пятиугольникаСкачать
Как разделить окружность на 10 частей How to divide a circle into 10 partsСкачать

Как нарисовать правильный пятиугольник | Видеоурок MATHANIMATIONСкачать

Построение шестнадцатиугольника циркулемСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать