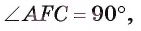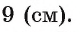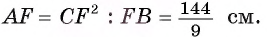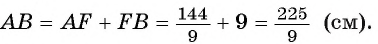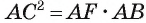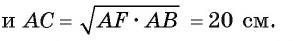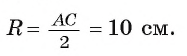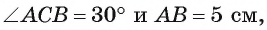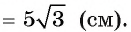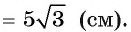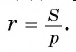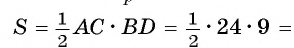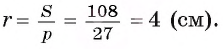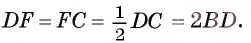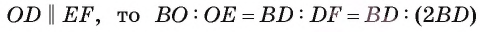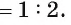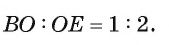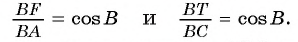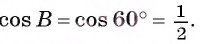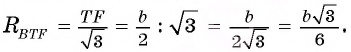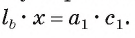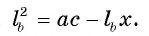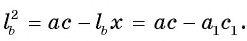Как решать задачи с окружностью вписанной в треугольник (5 видео)

Классификация задач на вписанные в треугольник и описанные около треугольника окружности

Разделы: Математика

Задачи на вписанные в треугольник и описанные около треугольника окружности вызывают даже у сильных учащихся затруднения при их решении. Попытка провести классификацию этих задач по содержанию и методам решения привела к положительным результатам. Учащиеся полюбили этот тип задач. Хотим поделиться нашим опытом.

Замечательное открытие: люди изобрели колесо.
Окружность, описанная около треугольника.
Окружность, вписанная в треугольник.
Задачи на вписанные и описанные окружности.

На востоке от Аравийского полуострова с севера на юг текут две большие реки – Евфрат и Тигр. Между ними тянется узкая длинная полоса земли. В древности она называлась Месопотамией, что в переводе означает “ Междуречье’’. Самым известным государством Месопотамии был Вавилон. Земля в Междуречье плодородная, но там не было ни металлов, ни камня, ни леса, чтобы строить дома. Всё это вавилонянам приходилось покупать у других народов. Поэтому Вавилон раньше других стран стал вести большую торговлю. Торговля помогала науке. В математике вавилонские учёные добились больших успехов.

Около шести тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо. Колесо? Что же тут замечательного? Но так кажется только на первый взгляд. Представьте себе на секунду, что вдруг случилось чудо, и на земле исчезли все колёса. Это было бы настоящей катастрофой! Остановятся автомобили и поезда, замрут заводы и фабрики, перестанут давать ток электростанции. Выходит, что неизвестный вавилонский изобретатель первого колеса действительно сделал великое открытие.

Вавилонские инженеры и мастера стали пользоваться блоками. Они поднимали и перетаскивали такие тяжести, справиться с которыми без колеса было бы не под силу. Колесо и рычаг стали первыми настоящими помощниками человека в работе с большими тяжестями.Так изобретение колеса сыграло очень большую роль в истории Вавилона.

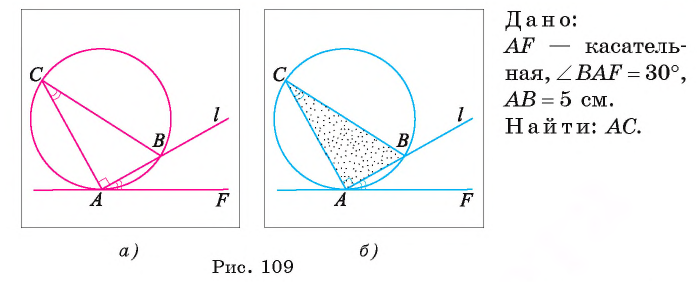
Окружность называется описанной около многоугольника, если все вершины многоугольника лежат в окружности.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. Около любого треугольника можно описать окружность.

Доказательство: Рассмотрим произвольный В треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=ОВ=ОС. Поэтому окружность с центром О радиуса ОА проходит через О все три вершины треугольника и, значит, является описанной около треугольника АВС.

Вывод: Центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:

а) в треугольнике, если он остроугольный;

б) на середине гипотенузы, если он прямоугольный;

в) вне треугольника, если он тупоугольный.

Рассмотрим задачи на нахождение радиуса описанной около треугольника окружности. (См. Приложение1.)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. В любой треугольник можно вписать окружность.

Доказательство: Рассмотрим произвольный треугольник АВС и обозначим М буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры А К В ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.

Так как точка О равноудалена A k B от сторон треугольника АВС то ОК = ОL=ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М.

Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ.

Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС.

Выводы. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника. Касательная к окружности (стороны треугольника) перпендикулярна к радиусу, проведённому в точку касания.

Рассмотрим задачи на нахождение радиуса вписанной в треугольник окружности.

Задачи на вписанную и описанную окружность. (См. Приложение 3.)

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Треугольники и окружность — задачи с примерами решения

Пример:

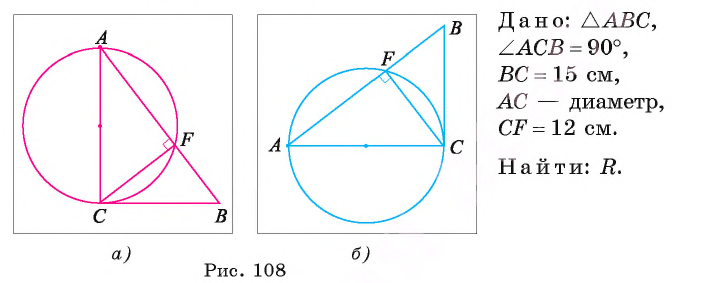
Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.

Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что

1) В треугольнике

2) Воспользовавшись равенством 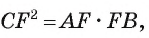найдем

3) Теперь

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,

Таким образом,

Пример:

Решение:

По теореме об угле между хордой и касательной 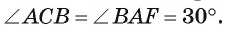Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как

Ответ

Пример:

Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 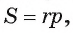где S — площадь треугольника, р — его полупериметр. Отсюда получим

1) Площадь треугольника

2) В прямоугольном треугольнике ADB длина катета

3) Теперь полупериметр

4) Таким образом, найдем

Пример:

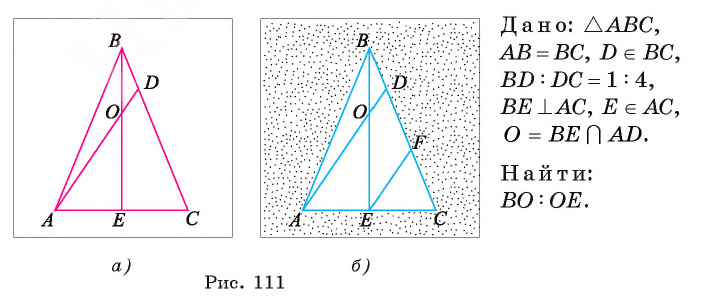
В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 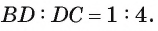В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

Решение:

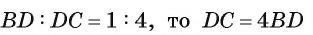
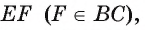
1) Так как (рис. 111, а, б). Проведем отрезок , параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,

4) Так как

Ответ:

Пример:

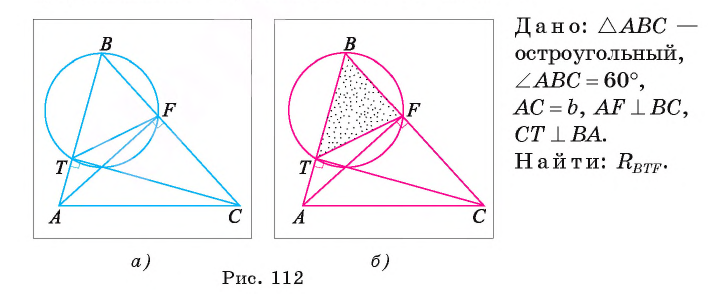
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.

Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

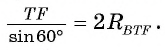
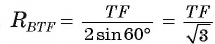
1) В треугольнике BTF по теореме синусов выполняется равенствоСледовательно, (рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,

Следовательно,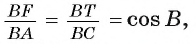т.е. треугольники подобны с коэффициентом подобия

3) Из подобия треугольников ABC и FTC следует, что 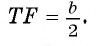Таким образом,

Ответ:

Пример:

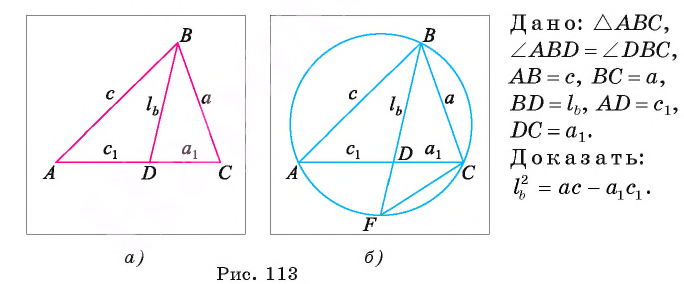
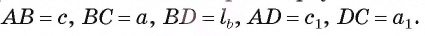
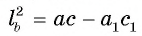
Отрезок BD — биссектриса треугольника ABC. Известно, что Докажите, что (рис. 113, а).

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство

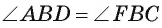
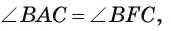
2) Треугольники ABD и FBC подобны, так как по условию и поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что 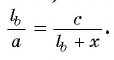Отсюда

3) Таким образом,

Что и требовалось доказать.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Площадь треугольника
Соотношения между сторонами и углами произвольного треугольника
Окружность и круг
Описанные и вписанные окружности
Пространственные фигуры — виды, изображения, свойства
Взаимное расположения прямых на плоскости
Треугольник
Решение треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.