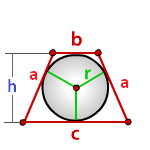
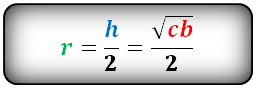
Формула для радиуса вписанной окружности равнобедренной трапеции (7 видео)

Радиус вписанной окружности в трапецию, формула

Радиус вписанной окружности в трапецию равен половине высоты трапеции.

Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:

Иначе в данную трапецию нельзя вписать окружность.

бедро трапеции выражается через высоту по теореме Пифагора:

Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).

после небольших преобразований получим

используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим

И соответственно радиус вписанной окружности в трапецию

Содержание

Радиус вписанной окружности в трапецию
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Признаки равнобедренной трапеции
Основные свойства равнобедренной трапеции
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
📹 Видео

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Радиус вписанной окружности в трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

Формула радиуса вписанной окружности равнобочной трапеции ( r ):

Калькулятор — вычислить, найти радиус вписанной окружности в равнобочную трапецию

Видео:Формулы для радиуса окружности #shortsСкачать

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Формула для радиуса вписанной окружности равнобедренной трапеции

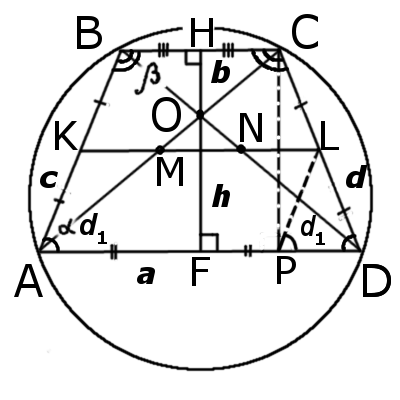Рис.1

Видео:Радиус описанной окружности трапецииСкачать

Признаки равнобедренной трапеции

∠ABC = ∠BCD и ∠BAD = ∠ADC

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Основные свойства равнобедренной трапеции

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

Видео:Задача про трапецию, описанную около окружностиСкачать

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

a = b + 2 h ctg α = b + 2 c cos α

b = a — 2 h ctg α = a — 2 c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d ₁ 2 — c 2	b =	d ₁ 2 — c 2	c = √ d ₁ 2 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b b =	2S	— a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	( a + b ) sin α

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√ 4 c 2 — ( a — b ) 2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Диагонали равнобедренной трапеции

Формулы длины диагоналей равнобедренной трапеции:

d ₁ = √ a 2 + c 2 — 2 ac cos α

d ₁ = √ b 2 + c 2 — 2 bc cos β

4. Формула длины диагонали через высоту и основания:

d ₁ =	1	√ 4 h 2 + ( a + b ) 2
	2

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√ 4 c 2 — ( a — b ) 2
	4

2. Формула площади через стороны и угол:

S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = ( a + b ) · r = √ ab ·c = √ ab ·m

6. Формула площади через диагонали и угол между ними:

S =	d ₁ 2	· sin γ	=	d ₁ 2	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
	4√ p ( p — a )( p — c )( p — d ₁)

где

p =	a + c + d ₁
	2

a — большее основание

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.