· Представление синусоидальных функций вращающимися векторами
Расчет переменных токов и напряжений с помощью алгебраических операций их мгновенных значений по исходным выражениям (1.1а) − (1.1в) весьма неудобен из-за громоздких вычислений. Графическое представление синусоидальных величин (см. рис.1.3) достаточно наглядно для одной, двух синусоид, но для сложных цепей практически не используется, ввиду трудности построения и анализа нескольких синусоидальных величин.
Представления синусоидальных функций при помощи вращающихся векторов (векторных диаграмм), как показано на рис 1.4, позволяет наглядно показать количественные и фазовые соотношения между разными напряжениями, токами и широко используется при объяснении процессов в цепях переменного тока.
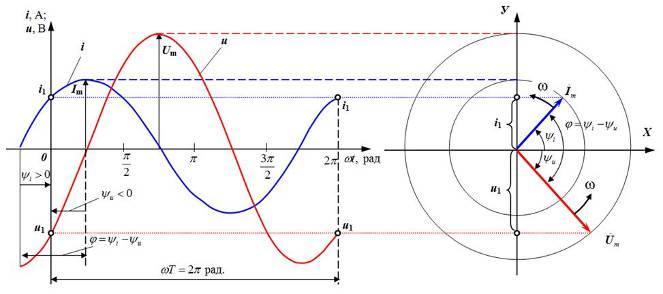
Мгновенное значение синусоидальной функции времени t или угла поворота wtможно представить в виде изменяющейся проекции на вертикальную ось вращающегося с угловой скоростью wвектора, как показано на рис 1.4. Векторы, изображающие синусоидальные функции времени, обозначаются, как и комплексные величины, точками вверху. Сравнивая рисунки 1.4,а и 1.4,б, можно видеть что длины векторов 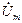
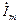
Рис.1.4. Соответствие синусоидальных функций u, i
и вращающихся векторов 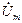
а) – графики мгновенных значений синусоидальных величин напряжения и тока; б)–вращающиеся с угловой скоростью ω векторы 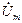
Проекции вращающихся с угловой скоростью ω векторов 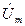
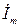
Углы наклона к оси абсцисс Х векторов 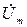
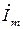
Начальные фазы yu и yi будут соответствовать углам наклона векторов 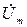
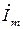
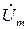
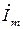
Так как фазовые сдвиги между напряжениями, токами и ЭДС одной частоты w остаются неизменными в течение времени, то от системы вращающихся векторов можно перейти к эквивалентной системе неподвижных векторов для момента времени t = 0.
В электротехнике принято оперировать действующими значениями величин напряжений U , ЭДС Е и токов I. Поэтому длины векторов на векторных диаграммах соответствуют не амплитудным, а действующим значениям, которые, как было выше сказано в 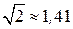
Углы наклона векторов напряжения 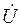
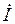
За положительное направление вращения векторов с угловой скоростьюw принято направление вращения против часовой стрелки (см. рис 1.4,б). Первый по вращению вектор считается опережающим следующий за ним вектор нафазовый угол j, который, в свою очередь, считается отстающим на тот же угол j относительно первого вектора. Например, на рис. 1.4,а вектор напряжения 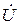
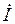
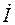
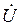
Если для синусоидальных величин одной частоты начальные фазы одинаковы, то векторы этих величин направлены в одну сторону, фазовый угол между ними равен нулю (j=0) и говорят, что эти величины совпадают по фазе (синфазны). Когда для синусоидальных величин разность фаз j = ±p, то векторы этих величин направлены в противоположные стороны и говорят, что эти величины противоположны по фазеили находятся в противофазе.
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, относящиеся к одной цепи, называют векторной диаграммой.
Применение векторных диаграмм делает наглядным анализ электрический цепи. В этом методе сложение и вычитание мгновенных значений синусоидальных величин можно заменить геометрическим сложением и вычитанием их векторов, по правилам, представленным в Приложении 4.
· Представление синусоидальных функций комплексными числами
Применение векторных диаграмм для анализа цепей переменного тока, несмотря на простоту и наглядность, не всегда дает достаточную точность при расчетах. Метод представления синусоидальных функций комплексными величинами и оперирование с ними как с комплексными числами, называемый комплексным методом [1], объединяет в себе простоту векторных диаграмм с возможностью производить расчеты с любой заданной степенью точности.
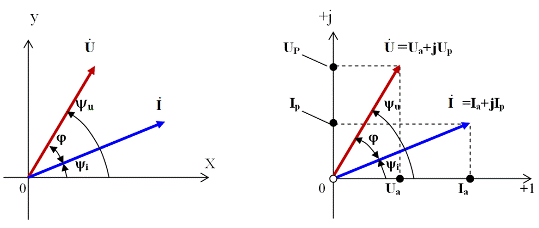
Комплексный метод основан на представлении векторов из декартовой системы координат (рис. 1.5,а) в комплексной плоскости (см. рис. 1.5,б) и на записи их комплексными числами. Это позволяет для цепей синусоидального тока применять законы Ома и Кирхгофа и методы расчета этих цепей в той же форме, что и для цепей постоянного тока, конечно с учетом специфики оперирования с комплексными величинами.
Рис. 1.5. Соответствие векторов и комплексных чисел
а) – векторы действующих значений тока I и напряжения U на векторной диаграмме;
б) – представление векторов тока и напряжения на комплексной плоскости
Синусоидальную функцию тока или напряжения можно однозначно изобразить соответствующим вектором в декартовых координатах (см. рис. 1.5,а) или на комплексной плоскости (рис. 1.5,б). В свою очередь, каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое можно записать в алгебраической, тригонометрической или показательной форме. Например, комплексы тока 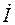
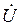
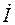
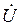
в тригонометрической форме:
и показательной форме:
где 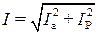
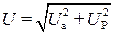
yi = arctgIр/Iа и yu = arctgUр/Uа – аргументы комплексовтока и напряжения, равные их начальным фазам; 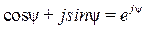
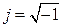
Примечание В электротехнике мнимая единица обозначается буквой j, в отличие от математики, где мнимая единица – i(а в электротехнике i– это принятое обозначение тока).
Таким образом, комплексное число или просто комплекс тока или напряжения в любой из выше перечисленных форм записи является отображением соответствующей синусоидальной функции тока или напряжения.
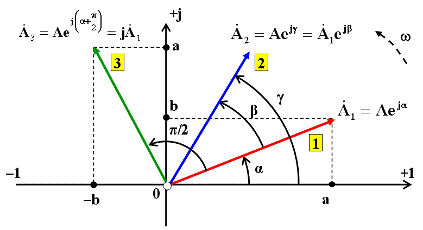
· Правила операций с векторами и комплексными величинами
Если исходный вектор 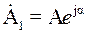
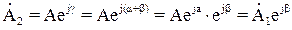
Рис. 1.6. Операция поворота вектора на комплексной плоскости
Следовательно, умножение комплексного числа 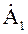
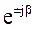
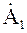
Если угол b = p/2= 90°, то из формулы Эйлера следует:
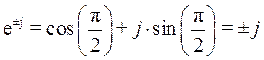
То есть умножение комплексного числа на мнимую единицу ±j соответствует повороту вектора на комплексной плоскости на угол ±p/2.
Если взять, например, комплекс в алгебраической форме 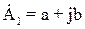
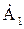
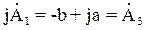
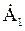
Считая угол поворотного множителя функцией времени, когда b = wt, получаем множитель или оператор вращения 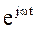
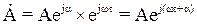
Комплексное число 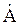
Операции сложения, вычитания, умножения и деления синусоидальных функций времени производят путем тех же алгебраических действий с соответствующими комплексными числами или векторами на комплексной плоскости. Переход от алгебраической формы записи комплексного числа к показательной форме, и наоборот, соответствует переходу от декартовых координат к полярным и от полярных координат – к декартовым. При этом операции алгебраического сложения и вычитания комплексных чисел, записанных в алгебраической форме, заменяются эквивалентными операциями геометрического сложения и вычитания соответствующих комплекс-векторов, записанных в показательной форме. Выбор той или иной формы записи комплексных чисел определяется простотой и удобством оперирования для определенной математической операции. Так, при сложении и вычитании комплексных чисел более удобна алгебраическая форма записи, а при умножении и делении – показательная.
Дата добавления: 2016-04-11 ; просмотров: 8383 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Лекция по электротехнике 3.2 - Изображение синусоидальной функции векторомСкачать

№14 Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы.
Пусть в прямоугольной системе координат имеется вектор длиной Im, расположенный под углом ψ к горизонтальной оси (рис. 14.1). Заставим этот вектор вращаться против часовой стрелки c угловой скоростью ω. Тогда за время t он повернется на угол ωt.
Проекцию вектора на вертикальную ось обозначим i. Из треугольника oab она равна i=Imsin(ωt+ψ), т.е. представляет собой функцию, определяющую мгновенное значение тока. Таким образом, последняя может быть представлена как проекция на вертикальную ось вращающегося вектора. Изображение тока с помощью вектора называется его векторной диаграммой. Длина вектора может быть равна амплитудному Im, либо действующему значению I.
Рис. 14.1 — Вращающийся вектор
Обычно вектор при этом показывается не в произвольный момент времени t, а в начальный (t = 0), когда его угол наклона к горизонтальной оси равен начальной фазе.
Теперь по уравнениям (2.3) построим векторную диаграмму двух векторов – тока и напряжения (2.4).
Длины векторов равны действующим значениям, углы их наклона к горизонтальной оси – начальным фазам, а угол между векторами, равный разности начальных фаз ψu и ψi, в соответствии с уравнением (2.4) определяет сдвиг фаз напряжения и тока.
Подчеркиваем, что на диаграмме стрелка, отмечающая угол φ, всегда направляется от вектора тока к вектору напряжения. Сейчас она направлена в положительном направлении – против часовой стрелки.
Рис. 14.2 — Векторная диаграмма тока и напряжения
Векторная диаграмма дает наглядное представление об отставании одних величин и опережении других. Если вращать картинку, показанную на рис. 14.2, против часовой стрелки, то вектор тока будет отставать от напряжения на угол φ. Так как при вращении длины векторов и угол между ними не меняются, то в том случае, когда начальные фазы напряжения и тока нас не интересуют, мы можем изображать диаграмму без осей и располагать ее так, как нам удобно (рис. 14.3).
Рис. 14.3 — Варианты построения векторной диаграммы
Видео:ТОЭ 26. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.Скачать

Часть III. Цепи синусоидального тока
Тема 3. Цепи синусоидального тока
- Общие сведения и определения
- Комплексная амплитуда
- Действующие значения синусоидальной функции
- Изображение синусоидальных функций векторами. Векторная диаграмма
- Изображение синусоидальной функции комплексными числами
- Закон Ома в комплексной форме
- Уравнения элементов в комплексной форме
- § 3.1. Общие сведения и определения:
Переменный ток имеет большее распространение, чем постоянный.
- конструкция электродвигателей и генераторов переменного тока гораздо проще;
- генераторы переменного тока могут быть выполнены для более высокого напряжения;
- переменный ток легко преобразовывается с помощью трансформатора, что необходимо при распределении электроэнергии и т.д.
Переменный ток – ток, периодически меняющий свое значение и направление. Наибольшее значение переменного тока – его амплитуда.
Переменный ток характеризуется:
Амплитуда – наибольшие (положительные или отрицательные) величины.
Период – время, в течение которого происходит полное колебание тока в проводнике.
Частота – обратно периоду.
Фаза – характеризует состояние переменного тока в любой момент времени.
Основным видом переменного тока является синусоидальный (гармонический) ток. Закон изменения такого тока описывается синусоидальной функцией.
В линейных электрических цепях, в которых действуют синусоидальные источники, все электрические параметры изменяются по синусоидальному закону.
ЭДС: 
Напряжение: 
Ток: 
e(t), u(t), i(t) – мгновенные значения;
ω = 2π – угловая частота, [рад/с];
ƒ = 1 Т – циклическая частота, [Гц];
Любую синусоидальную функцию можно изобразить в виде графика, который называется графиком временных значений или временной диаграммой.
- § 3.2. Комплексная амплитуда:
Расчет цепей синусоидального тока с использованием мгновенных значений требует громоздкой вычислительной работы и применим для простейших электрических цепей.
Для расчета цепей синусоидального тока синусоидальную функцию заменяют эквивалентной величиной.
где j = √ — 1 – мнимая единица.



Последняя запись означает, что синусоидальное напряжение можно представить на комплексной плоскости в виде двух векторов, длина которых равна Um и которые равномерно вращаются со скоростями, равными ω в противоположные стороны.
- § 3.3. Действующие значения синусоидальной функции:
Действующее значение синусоидальной функции – ее количественная оценка.
Действующие значения – среднеквадратичные за период значения синусоидальной функции, то есть, если:
то действующее значение:
Аналогично и для тока I и ЭДС ε .
Часто используются выражения, связывающие между собой амплитуду и действующее значение:
Действующее значение – это постоянная величина, которую обычно обозначают той же буквой, что и амплитуду, только без индекса m.
Действующее значение тока оказывает такое же тепловое действие на проводник с сопротивлением R , что и переменный ток, в течение времени, равном периоду. Поэтому большинство электроизмерительных приборов фиксируют и реагируют на действующие значения.
- § 3.4. Изображение синусоидальных функций векторами. Векторная диаграмма:
где a – проекция вектора на ось y в момент времени t.

Любому равномерно вращающемуся радиус-вектору соответствует некоторая синусоидальная функция, и наоборот.
Посмотрим, как условный графический образ синусоидальной функции – радиус-вектор – может быть применим при расчетах цепей переменного тока. Определим ток:
если: 

Как известно, сумма двух синусоид одинаковой частоты ω представляет собой также синусоиду частотой ω , то есть i = Imsin (ωt + ψ ) и, следовательно, задача сводится к нахождению амплитуды Im и начальной фазы Ψ суммарного тока i. Искомые параметры Im и Ψ можно найти, воспользовавшись известными тригонометрическими преобразованиями.
Проведем решение задачи с помощью радиус-векторов I1m и I2m , вращающихся с частотой ω, положение которых для момента времени t = 0 показаны на рисунке ниже и осуществим геометрическое суммирование этих радиус-векторов по правилу параллелограмма. Результирующий радиус-вектор Im будет вращаться с частотой ω и является изображением некоторой синусоидальной функцией времени.
Следовательно, i = i1 + i2 – геометрическое изображение искомого тока.
Измерив дугу суммарного радиус-вектора и, зная выбранный масштаб, можно определить амплитуду Im тока. Непосредственно по чертежу определяется и начальная фаза Ψ.
Рассмотренная совокупность радиус-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой.
- § 3.5. Изображение синусоидальной функции комплексными числами:

Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:
- алгебраической:
- тригонометрической:
- показательной:
( e – основание натурального логарифма).
Все три формы записи в соответствии с формулой Эйлера равнозначны:
Переход от одной формы записи к другой:
где a1 – действительная часть;
Запишем в трех формах выражение для единичных действительных и мнимых комплексных чисел ( A = 1 ):
где C = AB .
Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением:
Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока, а аргумент Ψ комплексного сопротивления – разности начальных фаз напряжения и тока:
Закон Ома в комплексной форме соответственно для амплитудных и действительных значений:

Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
🌟 Видео
Представление комплексных чисел синусоидальными величинамиСкачать

Лекция 040-2. Комплексные числа. Представление синусоид комплексными числамиСкачать

Лекция по электротехнике 3.1 - Получение синусоидальной ЭДССкачать
Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Синусоидальный однофазный переменный токСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Видеолекция «Электрические цепи однофазного синусоидального тока»Скачать

Частотное и временное представление сигналов. Спектр. МодуляцияСкачать

Теоретические основы электротехники 30. Символический расчёт схем синусоидального тока.Скачать
AGalilov: Преобразование Фурье "на пальцах"Скачать
Векторная диаграммаСкачать

Урок 32 (осн). Сила. Единицы силы. Изображение силСкачать

Лекция 040-1. Основные понятия цепей синусоидального токаСкачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Расчет цепей переменного синусоидального тока | Метод комплексных амплитуд | Часть 3Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

3 2 Форма записи электротехнических величин переменного синусоидального токаСкачать

Построение векторной диаграммы. Цепь RLCСкачать

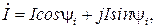
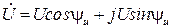
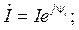
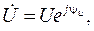
















 ( e – основание натурального логарифма).
( e – основание натурального логарифма).






