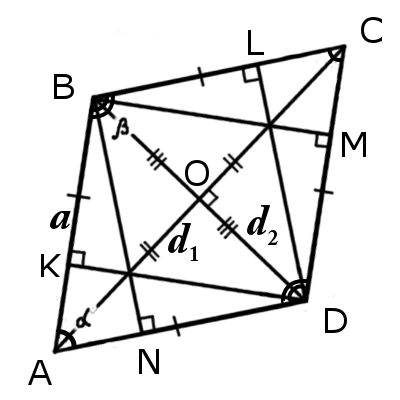
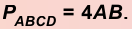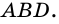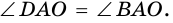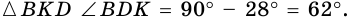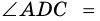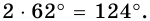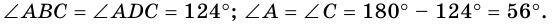 | 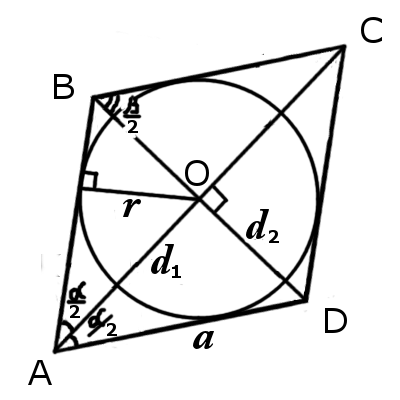 |
| Рис.1 | Рис.2 |
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- Диагонали ромба делят его углы пополам центром окружности
- Ромб и его свойства, определение и примеры с решением
- 🎦 Видео
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

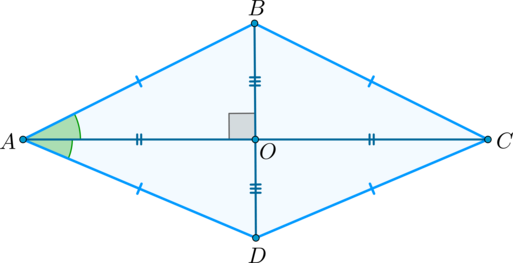
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:Геометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать

Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:Диагонали ромба пересекаются под прямым угломСкачать

Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:Площадь ромба. Легче понять...Скачать
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:Задание 24 ОГЭ по математике #9Скачать
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:Диагонали ромба точкой пересечения делятся пополам. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать

Диагонали ромба делят его углы пополам центром окружности
Определение
Ромб – это параллелограмм, у которого все стороны равны.
Таким образом, ромб обладает всеми свойствами параллелограмма:
(sim) противоположные углы ромба попарно равны;
(sim) соседние углы ромба в сумме дают (180^circ) ;
(sim) диагонали точкой пересечения делятся пополам.
Теорема: свойство ромба
Диагонали ромба перпендикулярны и делят его углы пополам.
Доказательство
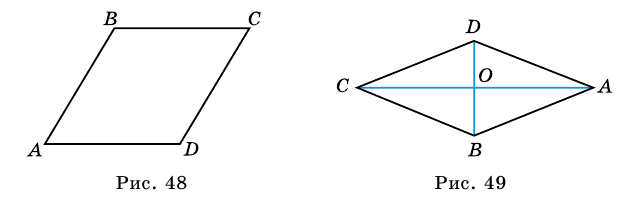
Рассмотрим ромб (ABCD) .
По определению ромба (AB = AD) , поэтому треугольник (BAD) равнобедренный. Так как ромб – параллелограмм, то его диагонали точкой (O) пересечения делятся пополам. Следовательно, (AO) – медиана равнобедренного треугольника (BAD) , а значит, высота и биссектриса этого треугольника. Поэтому (ACperp BD) и (angle BAC = angle DAC) .
Теорема: признаки ромба
1. Если в параллелограмме диагонали перпендикулярны, то это – ромб.
2. Если в параллелограмме диагонали делят его углы пополам, то это – ромб.
3. Если в выпуклом четырехугольнике все стороны равны, то он – ромб.
Доказательство
1) Рассмотрим параллелограмм (ABCD) . Пусть (ACperp BD) .
Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – высота (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD) . Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.
2) Пусть (AC) – биссектриса угла (angle A) .
Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – биссектриса (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD) . Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.
3) Пусть (ABCD) – произвольный четырехугольник и (AB=BC=CD=AD) .
Т.к. противоположные стороны четырехугольника попарно равны, то он – параллелограмм. Т.к. у него все стороны равны, то по определению это ромб.
Видео:Диагонали ромбаСкачать

Ромб и его свойства, определение и примеры с решением
Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).
Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.
1. Сумма любых двух соседних углов ромба равна 180°.
2. У ромба противолежащие углы равны.
3. Диагонали ромба точкой пересечения делятся пополам.
4. Периметр ромба
Кроме того, ромб имеет еще и такое свойство.
5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Доказательство:
Пусть 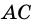
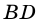
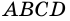
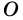
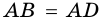
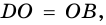
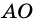
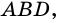
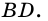
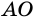
Следовательно, 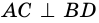
Аналогично можно доказать, что диагональ АС делит пополам угол 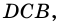
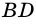
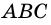
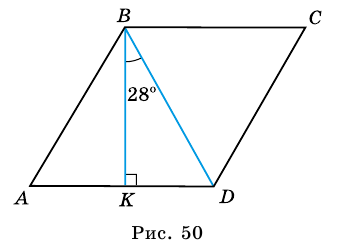
Пример:
Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.
Решение:
Пусть 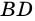
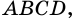
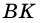
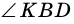
1) В
2) Так как 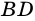
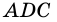
3) Тогда
Ответ. 124°, 56°, 124°, 56°.
Рассмотрим признаки ромба.
Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.
Доказательство:
1) Пусть 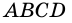
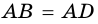
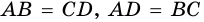
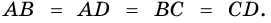
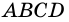
2) Пусть 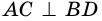
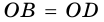
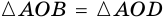
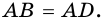
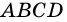
3) Диагональ 
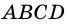
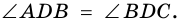
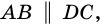
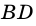
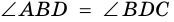
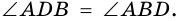
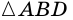
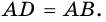
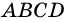
Пример:
Докажите, что если в четырехугольнике все стороны равны, то этот четырехугольник — ромб.
Доказательство:
Пусть 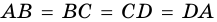
1) Так как противолежащие стороны четырехугольника 
2) У параллелограмма 
Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.
В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
- Площадь параллелограмма
- Прямоугольник и его свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
№408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимноСкачать

Задание 24 РомбСкачать

ОГЭ Задание 24 Диагонали ромбаСкачать

Диагонали ромбаСкачать

№477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромбаСкачать

Геометрия Признак ромба Если диагональ параллелограмма является биссектрисой его угла, то этотСкачать

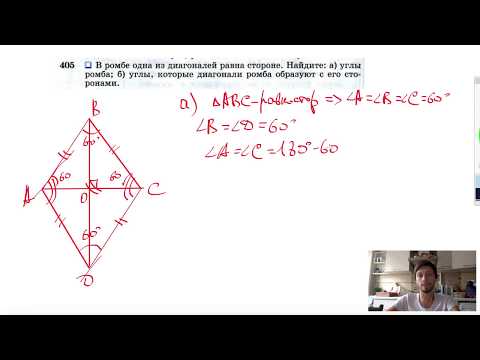
№405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы,Скачать
№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать

№1040. Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба.Скачать

8 класс, 8 урок, Ромб и квадратСкачать

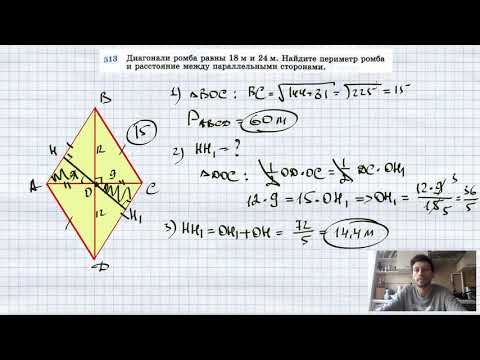
№513. Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба и расстояние между параллельными стоСкачать