- Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
- Детали машин
- Геометрические параметры эвольвентного зацепления
- Начальные окружности
- Делительная окружность
- Окружной шаг зубьев
- Основной шаг
- Окружная толщина зуба и окружная ширина впадины
- Окружной модуль зубьев
- Высота головки и ножки зуба
- Длина активной линии зацепления
- Коэффициент торцового перекрытия
- Модуль зубьев зубчатого колеса: расчет, стандартные, определение
- Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
- Зубчатые передачи
- Типы зубчатых передач
- Эвольвентное зацепление
- Форма зубьев
- Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
- Коррегирование зубчатого зацепления
- Зубчатые передачи с точно заданным межосевым расстоянием
- Зубчатые передачи с изменяемым межосевым расстоянием
- Расчетные формулы для зубчатых передач
- Степени точности зубчатых передач (DIN 3961…..3964)
- Зубчатые передачи стартера
- Модули зубчатых передач стартеров
- Стандарты зубчатых передач США
- Полная высота зуба
- Ножка зуба
- Система обозначений и преобразований
- Расчет наибольшего допустимого давления зубчатых передач
- Величины и единицы измерения для расчета наибольшего допустимого давления
- Коэффициент срока службы ф
- Расчет зубчатого зацепления на изгиб и разрушение зуба
- Коэффициент профиля зуба YFa
- Скоростной фактор fv
- Примерный расчет элементов зубчатого колеса
- Вычерчивание контура зуба
- Определение основных геометрических параметров зубчатых колес
- Модуль зуба – Модуль шестерни. Формулы расчёта
- Как определить модуль шестерни с прямым и косым зубом
- Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
- Смотреть что такое “Модуль зубчатого колеса” в других словарях:
- Модуль зуба что такое
- Модуль зубьев зубчатого колеса
- Что такое модуль зубчатого колеса
- Что же такое модуль шестерни?
- Формула расчета параметров прямозубой передачи
- Исходные данные и замеры
- Результаты расчетов
- Расчет параметров колеса и шестерни косозубой передачи
- Расчёт модулей зубчатых колёс
- 🎦 Видео
Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
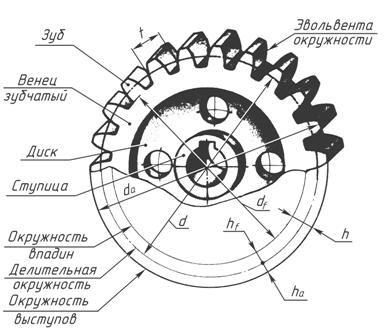
где z – число зубьев;
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
где t – шаг зацепления.
где h a – высота головки зуба, h a = m ; h f – высота ножки зуба, h f = 1,25 m .
Диаметр окружности выступов зубьев :
Диаметр окружности впадин :
Служит для передачи вращения при параллельных осях валов.
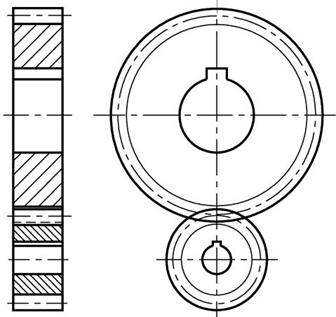
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2 .
Служит для преобразования вращательного движения в возвратно-поступательное.
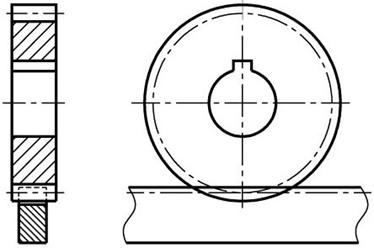
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
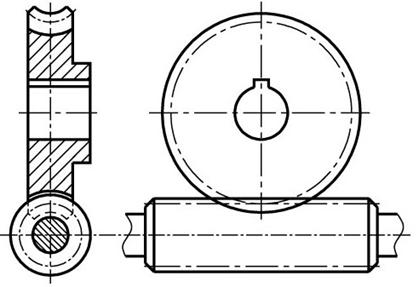
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
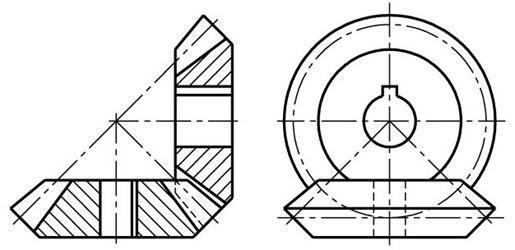
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Видео:Физика - движение по окружностиСкачать

Детали машин
Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Геометрические параметры эвольвентного зацепления
Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.
В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:
- w – начальной;
- b – основной;
- a – вершин зубьев;
- f – впадин зубьев.
Параметрам, относящимся к делительной окружности, индекс не присваивается.
При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу.
Начальные окружности
Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О1 и О2 до полюса П ) при неизменном межосевом расстоянии О1О2 тоже остается неизменным.
При изменении межосевого расстояния aw меняются и диаметры dw начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.
Межосевое расстояние определяется по формуле:
Делительная окружность
Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.
Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.
У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:
Исключение составляют передачи с угловой модификацией.
Окружной шаг зубьев
Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.
Основной шаг
Этот параметр, обозначаемый pb , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу pb .
Из треугольника О2ВП (см. рис. 1) диаметр основной окружности db2 = 2 rb2 = d2 cos αw , откуда основной шаг может быть определен по формуле:
Окружная толщина зуба и окружная ширина впадины
Окружная толщина зуба st и окружная ширина впадины et по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер st назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда st + et = p .
Окружной модуль зубьев
Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,
Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:
d = mz или m = d/z .
Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.
Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).
При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.
Высота головки и ножки зуба
Делительная окружность делит зуб по высоте на головку ha и ножку hf . Для создания радиального зазора с (см . рис. 1) необходимо
Для передачи без смещения ha = m .
Длина активной линии зацепления
При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S’S» линии зацепления называют длиной активной линии зацепления и обозначают gα . Длину gα легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S» и замеряют gα .
Коэффициент торцового перекрытия
Коэффициентом торцового перекрытия εα называют отношение длины активной линии зацепления к основному шагу:
где z1 и z2 – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.
Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.
За период работ пары зубьев точка их зацепления проходит путь, равный по длине gα (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу pb . При gα > pb необходимое перекрытие зубьев обеспечивается.
По условию непрерывности зацепления должно быть εα > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия εα .
Видео:Вращательное движение. 10 класс.Скачать

Модуль зубьев зубчатого колеса: расчет, стандартные, определение
Видео:Зубонарезание для чайников за 6 минут. Часть I - теорияСкачать

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:
- d = m × z,
- где z – число зубьев;
- m – модуль.
- Модуль зацепленияm – это часть диаметра делительной окружности, приходящейся на один зуб:
- m = t / π,
- где t – шаг зацепления.
- Высота зуба:
- h = ha + hf,
- где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
- Диаметр окружности выступов зубьев:
- da = d + 2ha = m(z + 2).
- Диаметр окружности впадин:
- df = d – 2hf = m(z – 2,5).
- Служит для передачи вращения при параллельных осях валов.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для преобразования вращательного движения в возвратно-поступательное.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращательного движения между валами со скрещивающимися осями.
- ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
- Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
- Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращения при пересекающихся осях валов.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Видео:Как определить шестернюСкачать

Зубчатые передачи

Типы зубчатых передач
Эвольвентное зацепление
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
 |  |
Форма зубьев

Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
 |  |
Коррегирование зубчатого зацепления

Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач
Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модули зубчатых передач стартеров
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением.
Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х.
(Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
- Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
- Р = z/d = z/(z • m/25,4) =25,4/m
- Для перевода стандарта США в европейский стандарт служит зависимость:
- m = 25,4 мм / P
- Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
- CP = (25,4 мм / P) π.
- Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
- Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
- Обозначение (пример): Р 5 /7
- Р = 7 для расчета головки зуба,
- Р = 5 для расчета других параметров.
Система обозначений и преобразований
- Диаметр окружности выступов: OD = da.
- Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
- Диаметр окружности впадин: RD = df
- Начальный диаметр:
- LD =(N+2x) / P (в дюймах)
- или
- LD= (N+2x)·m (в мм).
- LD ≈ dw,
- где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1.
В случае зубчатого зацепления с z1 Читайте также: Приспособление для снятия пружин подвески своими руками
При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
- Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1).
Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
В следующей статье я расскажу об электрических свойствах материалов.
Видео:Геометрические параметры зубчатых колёс. Перекрытие. Смещение.Скачать

Примерный расчет элементов зубчатого колеса
Длина всякой окружности равна ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой Πd,.
Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.
Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,
Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.
Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.
Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.
Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m. Выразим через модуль правую часть формулы:
- De = mz + 2m = m (z + 2) следовательно
- m = De : (z +2)
Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.
- Di = d — 2h»
- Высоту h» ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для Di получим
- Di = mz — 2 × 1,25m = mz — 2,5m или
- Di = m (z — 2,5m)
- Вся высота зуба h = h’ + h» т.е
- h = 1m + 1,25m = 2,25m
- Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.
Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) — равной приблизительно половине шага t зацепления, т. е. 1,57m.
Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t = s + sв) (Величину шага t определяем по формуле t/Π = m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.
- sв = 3,14m — 1,53m = 1,61m A для колес с обработанными зубьями.
- sв = 3,14m — 1,57m = 1,57m
Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:
Толщина обода e = t/2
Диаметр отверстия для вала Dв ≈ 1/в De Диаметр ступицы Dcm = 2Dв Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t Толщина диска К = 1/3b Длина ступицы L = 1,5Dв : 2,5Dв
Размеры t1 и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).
Модули (согласно ГОСТ 9563-60) Таблица №42.
Нормальные линейные размеры. Таблица №43. (Выдержка из ГОСТ 6636-60)
Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.
Вычерчивание контура зуба
Видео:6.3 Зубчатые цилиндрические передачиСкачать

Определение основных геометрических параметров зубчатых колес
- Лабораторная работа 10
- Цель работы — ознакомиться с практическими методами определения основных параметров зубчатых колес.
- Краткие теоретические сведения
Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль т, число зубьев z, угол зацепления а, величина смещения инструментальной рейки при нарезании зубчатого колеса.
Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.
Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты: нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 2.5.1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.
Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку А0, точка В — в точку В0 и точка D — в точку D0. Тогда
Таким образом, измерив вначале длину общей нормали Wzn (мм), соответствующей числу зубьев z„, а затем размер Wzn+ь охватив губками штангенциркуля на один зуб больше, рь
шаг по основной окружности — определим как разность двух измерений:
Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.
Рис. 2.5.1. Схема замера
Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 2.5.1).
| Число зубьев колеса | 12-18 | 19-27 | 28-36 | 37-45 | 46-54 | 55-63 | 64-72 | 73-81 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Модуль зацепления определим по формуле
Полученное значение модуля сопоставим со стандартным значением (табл. 2.5.2) и примем его ближайшее значение.
| т, мм | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 | 3,25 |
| Рь, мм | 5,904 | 6,642 | 7,380 | 8,818 | 8,856 | 9,954 |
| т, мм | 3,50 | 3,75 | 4,00 | 4,50 | 5,00 | 5,50 |
| Рь, мм | 10,33 | 11,07 | 11,808 | 13,28 | 14,76 | 16,84 |
По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям.
Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для колеса, нарезанного без смещения, и найти коэффициент смещения инструментальной рейки:
где sb = Wzn+l — znpb — толщина зуба по основной окружности данного колеса; sb = mcosa(^ + zinva) — толщина зуба по основной окружности зубчатого колеса, нарезанного при х = 0; a = 20°; inv 20° = 0,0149.
При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.
Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2.5.2, а) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 2.5.2, б.
Рис. 2.5.2. Определение диаметров при четном (а) и нечетном (б) числе зубьев
Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни ((/0Тв) и размер//’. Тогда диаметр окружности выступов
Аналогично измеряется диаметр окружности впадин:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент — штангенциркуль.
Порядок выполнения работы
- 1. Подсчитать число зубьев колеса z.
- 2. По табл. 2.5.1 определить число зубьев z„, которые следует охватить штангенциркулем.
- 3. Измерить штангенциркулем Wzn и Wzn+ (рис. 2.5.1). Для большей точности обмерять нужно трижды на разных участках зубчатого венца. Окончательные значения Wzn и Wzn+ есть среднеарифметическое трех обмеров. По формуле (2.5.1) определить величину шага рь по основной окружности.
- 4. По формуле (2.5.2) найти модуль зацепления в миллиметрах, округлив его величину до ближайшего стандартного значения согласно табл. 2.5.2. В формуле 2.5.2 угол исходного контура а = 20°.
- 5. Учитывая, что есть колеса с углом а = 15°, выполнить проверочный расчет модуля по выражению
измерив диаметр da окружности вершин.
6. Измерить d/диаметр окружности впадин.
Примечание: da и df при четном числе z измерить штангенциркулем (рис. 2.5.2, а), при нечетном числе — найти в соответствии с рис. 2.5.2, б по формулам:
- 7. Определить:
- а) шаг по делительной окружности
б) диаметр делительной окружности
в) диаметр основной окружности
г) делительную высоту головки зуба
д) делительную высоту ножки зуба
е) коэффициент высоты головки зуба
ж) толщину зуба по основной окружности
- 8. По формуле (2.5.3) рассчитать коэффициент смещения х исходного контура, с которым нарезалось данное колесо.
- 9. Определить толщину зуба по основной окружности:
Контрольные вопросы и задания
- 1. Что такое модуль зубчатого колеса?
- 2. Как определить шаг зубчатого колеса?
- 3. Дайте понятие основной и делительной окружностей.
- 4. Какова зависимость между числом зубьев и диаметром зубчатого колеса?
- 5. Что называется коэффициентом смещения исходного контура?
- 6. Как изменяются основные параметры зубчатого колеса при смещении исходного контура?
- 1. Число зубьев z = …
- 2. Определение шага и модуля зацепления:
| Номер измерения | Wz,,+ь мм | Wzn, мм |
| Среднее |
* число zn выбирается по табл. 2.5.1.
Шаг зацепления по основной окружности pb = WZfJ+1 — Wzn = … мм.
Модуль т = ——— = … мм.
Модуль, уточненный по табл. 2.5.2, т = … мм.
Шаг зацепления по делительной окружностир = пт = … мм.
Шаг по основной окружности (уточненный)рь=р cos а= … мм.
- 3. Диаметр делительной окружности d = mz= … мм.
- 4. Диаметр основной окружности db = d cos а= … мм.
- 5. Определение действительной толщины зуба по основной окружности sb = Wzn +1 -znpb = … мм.
- 6. Расчет толщины зуба по основной окружности нулевого колеса:
7. Определение коэффициента смещения:
9. Определение диаметров окружностей вершин da и впадин df колеса:
| Номер измерения | doiB | Н’ | da | Н» | df | Расчётные формулы при нечётном числе z |
| Среднее |
10. Учитывая, что есть колеса с углом зацепления а = 15°, в и. 2 выполнить проверочный расчет модуля по выражению (для нормального колеса)
11. Определение коэффициента высоты головки зуба колеса, зубья которого нарезаны без смещения:
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Модуль зуба – Модуль шестерни. Формулы расчёта
Шаг зубьев ρ так же, как и длина окружности, включает в себя трансцендентное число π, а потому шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число ρ/π, которое называют модулем зубьев т и измеряют в миллиметрах:
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезного инструмента значения m регламентированы стандартом (табл. 8.1).
Высота головки и ножки зуба. Делительная окружность рассекает зуб по высоте на головку ha и ножку hf. Для создания радиального зазора с (см. рис. 8.19)
Для нормального (некорригированного) зацепления ha = m. Длина активной линии зацепления. При вращении зубчатых колес точка зацепления S (см. рис. 8.9) пары зубьев перемещается по линии зацепления NN.
Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S” пересечения линии зацепления с окружностью вершин шестерни. Отрезок S’S” линии зацепления называется длиной активной линии зацепления и обозначается ga.
Длину ga легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S” и замеряют ga.
Коэффициент торцового перекрытия. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи.
Как определить модуль шестерни с прямым и косым зубом
Часто мне задают вопрос: Как определить модуль косозубой шестерни. Один из самых простых вариантов — обкатать фрезой, то есть методом подбора, вставить в шестерню фрезу и посмотреть совпадает ли шаг! Этот вариант подходит для шестернь малого модуля, для более больших шестернь требуются формулы расчёта.
Давайте определим модуль косозубой шестерни. В качестве примера я возьму небольшую шестерню. Данный метод идентичен и для более больших шестернь и больших модулей.
- Есть вот такая шестерня:
- Допустим что фрезы обкатать у нас на данный момент нет и вообще хочется просто посчитать по формуле!
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
- Можно использовать и другой вариант — высота зуба делится на 2,25.
- Я обычно или обкатываю фрезой или считаю по формуле — модуль = De/Z+2.
- Таким образом можно определить модуль как косозубой шестерни, так и шестерни с прямым зубом.
- Поделится, добавить в закладки!
- zuborez.info
Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
Модуль зубчатого колеса геометрический параметр зубчатых колёс.
Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π.
Для косозубых цилиндрических колёс различают: окружной модуль ms = dд/z = ts/π, нормальный модуль mn = tn/π, осевой модуль ma = tа/π, где ts, tn и ta— соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к.
стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Модуль высокоэластический
- Модуль расстояния
Смотреть что такое “Модуль зубчатого колеса” в других словарях:
- МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
- модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
- нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
- нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
- окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
- расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
- Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
- Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Модуль зуба что такое
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня».
За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки.
Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
- Для расчета этого параметра применяют следующие формулы:
- m=t/π,
- где t — шаг.
- Параметры зубчатых колес
- Модуль зубчатого колеса можно рассчитать и следующим образом:
- m=h/2,25,
- где h — высота зубца.
- И, наконец,
- m=De/(z+2),
- где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
- Расчет модуля зубчатого колеса
- Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
- π×D=t×z,
- проведя преобразование, получим:
- D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
- t/π=m,
- размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
- В=m×z;
- выполнив преобразование, находим:
- m=D / z.
- Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
- De=d+2× h’,
- где h’- высота головки.
- Высоту головки приравнивают к m:
- h’=m.
- Проведя математические преобразования с подстановкой, получим:
- De=m×z+2m = m(z+2),
- откуда вытекает:
- m=De/(z+2).
- Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
- Di=D-2h“,
- где h“- высота ножки зубца.
- Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
- h’ = 1,25m.
- Устройство зубчатого колеса
- Выполнив подстановку в правой части равенства, имеем:
- Di = m×z-2×1,25m = m×z-2,5m;
- что соответствует формуле:
- Di = m(z-2,5m).
- Полная высота:
- h = h’+h“,
- и если выполнить подстановку, то получим:
- h = 1m+1,25m=2,25m.
- Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
- Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
- Для более крупных потребуются измерения и вычисления.
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Видео:Центростремительное ускорение. 9 класс.Скачать

Расчёт модулей зубчатых колёс
Перейти к загрузке файла
| № зубчатого колеса | Число зубьев | Модуль, мм | Диаметр делительной окружности, мм | Ширина зубчатого венца, мм |
| 1 | 18 | 2 | 36 | 52 |
| 2 | 36 | 2 | 72 | 52 |
| 3 | 20 | 2 | 40 | 52 |
| 4 | 50 | 2 | 100 | 52 |
| 5 | 35 | 2 | 70 | 52 |
| 6 | 35 | 2 | 70 | 52 |
| 7 | 20 | 2 | 40 | 65 |
| 8 | 64 | 2 | 128 | 65 |
| 9 | 56 | 2 | 112 | 65 |
| 10 | 28 | 2 | 56 | 65 |
Расчёт на контактную выносливость рабочих поверхностей зубьев
Действующие в передаче контактные напряжения определяют по формуле
где ун — контактные напряжения, МПа; zН — коэффициент, зависящий от угла наклона зубьев, для x=0 применяем zН=1,76; zМ — коэффициент, учитывающий механические свойства материалов сопряжённых колёс, для стальных колёс zМ=275; zе — коэффициент, учитывающий суммарную длину контактных линий:
Коэффициент торцевого перекрытия:
где z1 и z2 — числа зубьев шестерни и колеса, знак «+» принимают для наружного зацепления.
Удельную расчётную окружную силу щHt определяют по формуле
где Pt — исходная окружная сила, Н:
где щHV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм.
Допускаемое контактное напряжение [ун] определяем по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kHL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kHL=1.
- Для стали 45 с улучшением =750 МПа.
- 532,25 МПа ? 750 МПа
- Условие контактной выносливости выполняется.
- Расчёт на изгибную выносливость зубьев
- Действующее в передаче напряжение изгиба сравнивается с допустимыми, с учётом коэффициента долговечности.
- Действующее напряжение изгиба:
Коэффициент yе — учитывает перекрытие зубьев. Для прямозубых колёс применяют yе=1. Коэффициент yв учитывает наклон зуба. Для прямозубых применяют yв=1.
Удельную расчётную окружную силу щFt определяем по формуле
где Pt — расчётная окружная сила в зубчатом зацеплении, Н; bщ — рабочая ширина венца, мм
Окружная сила Pt=2•103•M1/d1, где M1 — крутящий момент, Н•м; d1 — диаметр делительной окружности, мм.
Коэффициент kFa учитывает распределение нагрузки между зубьями. Для прямозубых передач приметаем kFa=1. Коэффициент kFв учитывает распределение нагрузки по ширине венца, можно принять kFв=1.1.
Коэффициент kFv учитывает динамическую нагрузку, возникающую в зацеплении.
где щFV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм; для прямозубых передач д=0.016; коэффициент g =47, учитывает влияние разности шагов зацепления.
Допускаемое изгибное напряжении [уF] определяется по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kFL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kFL=1.
Для стали Для стали 45 с улучшением у‘F=450 МПа, условие изгибной выносливости выполняется.
265.49 МПа ? 450 МПа
Условие на изгибную выносливость выполняется.
🎦 Видео
Лекция 4. Конические зубчатые передачиСкачать

шестерни для Philips определение коррекции, модуля и основные понятияСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Механические передачи. Часть 1. История. Геометрия зубчатых колесСкачать

3d печать ШЕСТЕРНИ. ТЕОРИЯ И ПРАКТИКА. Модульная и питчевая системыСкачать

Ременная передача. Урок №3Скачать

Лекция «Цилиндрические зубчатые передачи. Основные параметры»Скачать

Лекция 5. Червячные передачиСкачать

Координаты вектора. 9 класс.Скачать

Штангензубомер ШЗН-18. Как измерить зуб шестерни?Скачать

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.





 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
 Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:
Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:









