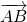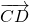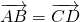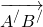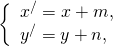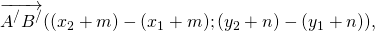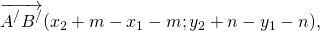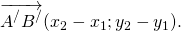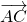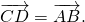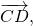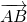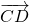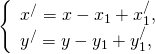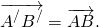Если векторы равны тогда верно что (2 видео)

Равные вектора

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

рис. 1

Содержание

Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
Примеры пространственных задач на равенство векторов
Векторы, имеющие равные длины
Равные векторы
Противоположно направленные векторы
Физика, равные по модулю противоположно направленне векторы
Равные векторы
🔥 Видео

Видео:№752. Верно ли утверждение: а) если вектор a = вектору b, то a⇈bСкачать

Примеры задач на равенство векторов

Примеры плоских задач на равенство векторов

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2 n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2 n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Векторы, имеющие равные длины

Рассмотрим векторы, имеющие равные длины. Если такие векторы сонаправлены, их называют равными.

У равных векторов совпадает и длина и направление.

Векторы, направленные в противоположные стороны, даже, если у них будут равные длины, равными назвать не получится.

Если совпадает только одна характеристика — длина, то векторы называют равными по модулю.

Видео:№750. Докажите, что если векторы АВ и СD равны, то середины отрезков AD и ВС совпадают.Скачать

Равные векторы

Если два вектора равны (т. е. одинаковые), то у них одинаковые:

Рассмотрим рисунок 1. На рисунке представлены векторы, обозначенные красным и зеленым цветом. Видно, что векторы имеют равные координаты — проекции на оси. Длины проекций для этих векторов: на ось Ox = 2, на ось Oy = 3. Если векторы имеют равные соответственные проекции (координаты), то эти векторы равны.

Примечание:

Когда векторы равны, вместо одного из них мы можем использовать второй вектор. Если нам будет удобнее работать со вторым вектором.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Противоположно направленные векторы

Вектор можно развернуть в противоположную сторону. С точки зрения математики, для этого достаточно перед вектором дописать знак минус.

Пример 1:

Векторы ( vec ) и ( -vec ) развернуты в противоположные стороны.

Когда векторы обозначают двумя буквами, то:

Векторы ( overrightarrow ) и ( left( -overrightarrowright) ) направлены в противоположные стороны.

Вектор ( left(-overrightarrow right) ) — это вектор ( overrightarrow ).

На языке математики это записывают так: ( left(-overrightarrowright) = overrightarrow ).

Для вектора ( overrightarrow ): точка A — начальная, B — конечная.

А для вектора (overrightarrow ) наоборот: точка B — начальная, A — конечная.

Когда даны координаты вектора, то, чтобы его развернуть в противоположную сторону, нужно изменить знак каждой его координаты на противоположный.

Пример 2:

Примечание:

Если равны только длины векторов, а направлены они в противоположные стороны, знак равенства между ними записать не получится. Такие векторы не равны!

Видео:Равенство векторов. 9 класс.Скачать

Физика, равные по модулю противоположно направленне векторы

В физике, в третьем законе Ньютона, идет речь о равных по модулю и противоположно направленных векторах.

Вспомним третий закон Ньютона: ( vec<F_> = -vec< F_> ) – длины векторов равны, а направления противоположны.

Чтобы приравнять такие векторы, необходимо перед одним из них записать знак минус:

Видео:Угол между векторами. 9 класс.Скачать

Равные векторы

В различных школьных учебниках определение равных векторов даётся по-разному.

В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.

Два вектора называются равными, если они совмещаются параллельным переносом.

(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Например, изображенные на рисунке

Равенство векторов обозначают так:

(Свойства равных векторов)

1) Равные векторы сонаправлены и имеют равные длины.

2) Равные векторы имеют равные координаты.

3) От любой точки можно отложить вектор, равный данному, и притом только один.

1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.

2) Пусть дан вектор

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂).

По определению равных векторов, вектор

равный данному, получен из

Если этот параллельный перенос задан формулами

Найдём координаты каждого из векторов:

То есть координаты равных векторов

Что и требовалось доказать.

Таким образом, координаты задают длину и направление вектора, но не фиксируют его.

3) Пусть даны вектор

и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор

При таком параллельном переносе вектор

переходит в вектор

По определению равных векторов,

Что и требовалось доказать.

На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).

Например,

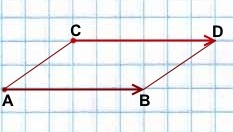
отложенный от точки C, равен вектору

(Признаки равенства векторов)

1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.

2) Если у векторов соответствующие координаты равны, то векторы равны.

1) Пусть векторы

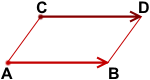
сонаправлены и имеют одинаковые длины.

Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор