Окружности радиусов 4 и 60 касаются

Геометрия | 5 — 9 классы

Окружности радиусов 4 и 60 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D — на второй.

При это AC и BD — общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

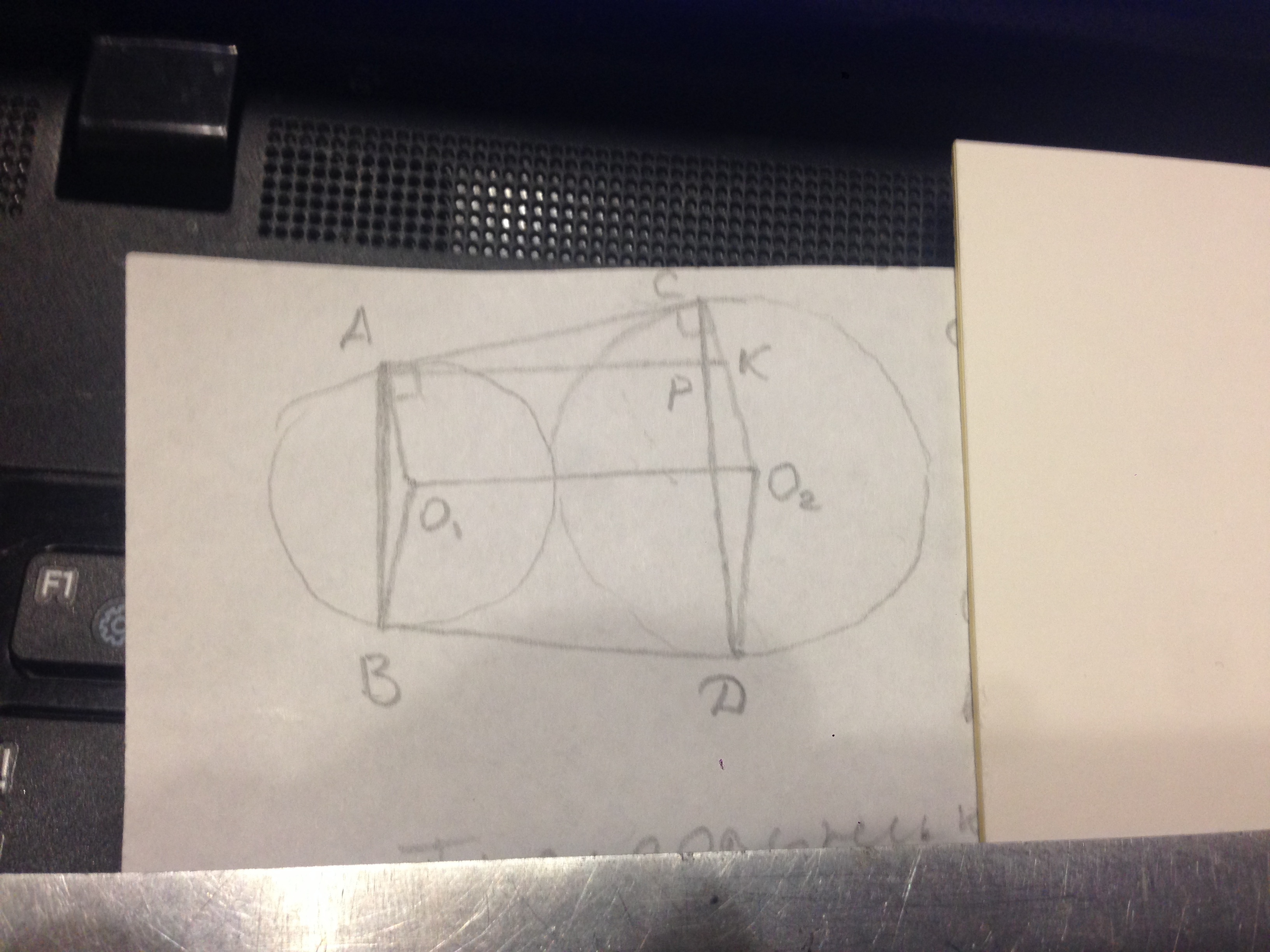
АО1 = 4, СО2 = 60, Найти АР.

О1О2 = 4 + 60 = 64.

Тр — ки АСК и CHR подобны, так как∠К — общий и оба прямоугольные, значит АК / СК = СК / РК⇒ РК = СК² / АК.

СК = СО2 — КО2 = 60 — 4 = 56.

АР = АК — РК = 64 — 49 = 15 — это ответ.

Видео:Радиус и диаметрСкачать

Две окружности касаются друг друга внешним образом в точке M?

Две окружности касаются друг друга внешним образом в точке M.

Общая внешняя касательная к этим окружностям касается их в точках A и B, причем MA = 8 ; MB = 6.

Определите радиусы окружностей.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность радиуса 2 внешне касается окружности меньшего радиуса?

Окружность радиуса 2 внешне касается окружности меньшего радиуса.

К этим окружностям проведена общая касательная, расстояние между точками касания равно 3.

Найдите радиус меньшей окружности.

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Окружности радиусов 3 и 6 с центрами соответственно в точках и O1 и O2 касаются внешним образом в точке A?

Окружности радиусов 3 и 6 с центрами соответственно в точках и O1 и O2 касаются внешним образом в точке A.

К окружностям проведены общая внешняя касательная и общая внутренняя касательная.

Эти касательные пересекаются в точке B, а L — общая точка внешней касательной и окружности радиуса 3.

Найдите R радиус окружности, вписанной в четырёхугольник ABLO2.

В ответ записать R(корень из 2 + 1).

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Две окружности с радиусами 5 и 3 касаются в точке О?

Две окружности с радиусами 5 и 3 касаются в точке О.

Их общая касательная, проходящая через точку О, пересекает внешние касательные этих окружностей в точках А и В соответственно.

Видео:Три окружности касаются прямой и друг друга внешним образомСкачать

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С, Найдите радиус окружности, описанной около треугольника АВС.

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

2 окружности радиусы которых 4 и 6 , касаются внешним образом, их общие внешние касательные пересекаются в точке М найдите расстояние до центра меньшей из окружностей?

2 окружности радиусы которых 4 и 6 , касаются внешним образом, их общие внешние касательные пересекаются в точке М найдите расстояние до центра меньшей из окружностей.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Две окружности касаются внешним образом в точке К?

Две окружности касаются внешним образом в точке К.

Прямая касается первой окружности в точке А, а второй – в точке В.

Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.

А) Докажите, что прямые AD и BC параллельны.

Б) Найдите площадь треугольника DКС, если известно, что радиусы окружностей равны 1 и 4.

Видео:Думаю... ( ° ͟ʖ °)Скачать

Окружность радиуса 4 касается внешним образом второй окружности в точке B общая касательная к этим окружностям проходящая через точку B пересекаются с некоторой другой их общей касательной в точке A н?

Окружность радиуса 4 касается внешним образом второй окружности в точке B общая касательная к этим окружностям проходящая через точку B пересекаются с некоторой другой их общей касательной в точке A найдите радиус окружности если AB равно 6.

Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Две окружности радиусами R и r касаются внешним образом в точке M?

Две окружности радиусами R и r касаются внешним образом в точке M.

К окружностям проведена общая внешняя касательная NK, где N и K — точки касания.

В криволенейный треугольник MNK вписана окружность.

Найдите ее радиус.

Видео:Геометрия В острый угол, равный 60, вписаны две окружности, извне касающиеся друг друга. РадиусСкачать

Окружности с радиусамии 6 и 2 касаются внешне?

Окружности с радиусамии 6 и 2 касаются внешне.

Найдите расстояние от точки касания до общей касательной к окружностям.

Перед вами страница с вопросом Окружности радиусов 4 и 60 касаются внешним образом?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

В основании правильной треугольной пирамиды лежит правильный (равносторонний) треугольник со стороной (a), а боковые грани пирамиды — равные равнобедренные треугольники. Площадь боковой поверхности пирамиды (Sбок)равна сумме площадей боковых граней ..

1миля(географическая) = 1 / 15 градуса земного экватора ≈ 7, 42км 1верста(путевая, или пятисотная) = 500 саженей ≈ 1066, 8м 1аршин(шаг) = 4 четверти = 28 дюймов = 16 вершков ≈ 71, 12см.

Посмотри внизу таблицу, по твоему вопросу не понятно, что надо.

Углы при меньшем основании : 35, 35. Углы при большем основании : 145, 145.

Нужно взять транспортир. И.

AD = AK + KD = 5 + 15 = 20 Д. П. CH (перпендкуляр AD) BC = KH AK = HD = 5 BC = KH = AD — AK — HD = 20 — 5 — 5 = 10 Ответ AD = 20 ; BC = 10.

AD = AK + KD = 20 BC = AD — 2AK = 10.

Sin B = cos A = 7 / 14 = 1 / 2.

Построй параллелограм и нарисуй указанные вектора. Получаем : BM = 1 / 2 * BO = 1 / 2 * (BA + AO) = 1 / 2 * (BA + 1 / 2 * AO) = 1 / 2 * BA + 1 / 4 * AO = — 1 / 2 * m + 1 / 4 * n.

Так как трапеция равнобокая, то проекция боковой стороны трапеции на большее основание равно (15 — 5) / 2 = 10 / 2 = 5 см. Отсюда косинус острого угла трапеции равен : cos A = 5 / 10 = 1 / 2. Тогда острый угол трапеции равен arc cos(1 / 2) = 60°. ..

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

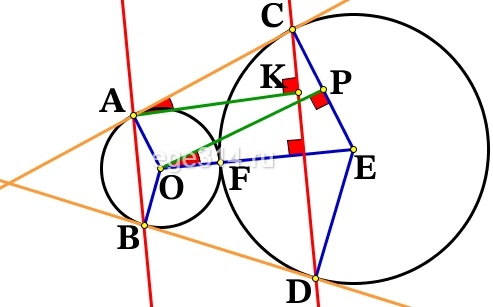
Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Окружности радиусов 4 и 60 касаются

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Разделы

Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Дополнительно

Задача по математике — 6823

На стороне $AB$ выпуклого четырёхугольника $ABCD$ отмечены точки $E$ и $F$, на стороне $BC$ — точки $K$ и $L$, на стороне $CD$ — точки $M$ и $N$, на стороне $AD$ — точки $P$ и $Q$. При этом $AE=EF=FB$, $BK=KL=LC$, $CM=MN=ND$ и $DP=PQ=QA$.
а) Докажите, что отрезки $KQ$ и $LP$ делят отрезок $FM$ на три равных отрезка.
б) Известно, что площадь четырёхугольника $ABCD$ равна 18. Найдите площадь четырёхугольника, вершины которого — точки пересечения прямых $EN$, $FM$, $KQ$ и $LP$.

Задача по математике — 6824

Общие внутренние касательные к двум окружностям перпендикулярны. Одна из них касается окружностей в точках $A$ и $C$, вторая — в точках $B$ и $D$ (точки $A$ и $B$ лежат на одной окружности).
а) Докажите, что отрезок $AC$ равен сумме радиусов окружностей.
б) Найдите площадь четырёхугольника $ABCD$, если известно, что $AB=6$, $CD=8$.

Задача по математике — 6825

Окружность с центром $O$ касается боковой стороны $AB$ равнобедренного треугольника $ABC$, продолжения боковой стороны $AC$ и продолжения основания $BC$ в точке $N$. Точка $M$ — середина основания $BC$.
а) Докажите, что $AN=OM$.
б) Найдите $OM$, если стороны треугольника $ABC$ равны 10, 10 и 12.

Задача по математике — 6826

Окружность с центром $O$, вписанная в треугольник $ABC$, касается стороны $BC$ в точке $M$. Окружность с центром $O_$ касается стороны $BC$ в точке $N$, а также касается продолжений сторон $AC$ и $AB$.
а) Докажите, что около четырёхугольника $BOCO_$ можно описать окружность.
б) Найдите площади четырёхугольников $BOCO_$ и $NOMO_$, если известно, что $AC=6$, $BC=8$, $AB=10$.

Задача по математике — 6827

Окружность с центром $O$ и окружность вдвое меньшего радиуса касаются внутренним образом в точке $A$. Хорда $AB$ большей окружности пересекает меньшую окружность в точке $M$.
а) Докажите, что $M$ — середина $AB$.
б) Луч $OM$ пересекает большую окружность в точке $P$. Найдите расстояние от центра большей окружности до хорды $AP$, если радиус большей окружности равен 13, а $OM=5$.

Задача по математике — 6828

Окружности с центрами $O_$ и $O_$ касаются внешним образом в точке $C$. К окружностям проведены общая внешняя касательная и общая внутренняя касательная. Эти касательные пересекаются в точке $D$.
а) Докажите, что треугольник $O_DO_$ прямоугольный.
б) Найдите радиусы окружностей, если известно, что $DO_=sqrt$ и $DO_=2sqrt$.

Задача по математике — 6829

В треугольник $ABC$ помещены две касающиеся окружности с центрами $O_$ и $O_$, причём первая из них касается сторон $AB$ и $AC$, а вторая — сторон $AB$ и $BC$.
а) Докажите, что прямые $AO_$ и $BO_$ пересекаются в центре окружности, вписанной в треугольник $ABC$.
б) Найдите радиусы окружностей, если известно, что они равны, а $AB=AC=10$ и $BC=12$.

Задача по математике — 6830

Две окружности касаются внешним образом в точке $K$. Прямая касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что $ADparallel BC$.
б) Найдите площадь треугольника $DKC$, если известно, что радиусы окружностей равны 1 и 4.

Задача по математике — 6831

В равнобедренной трапеции $ABCD$ с основаниями $AD$ и $BC$ расположены две окружности, каждая из которых касается другой окружности, двух боковых сторон и одного из оснований. Пусть $P$ и $Q$ — точки касания окружностей с боковой стороной $AB$, а общая касательная окружностей, проходящая через их точку касания, пересекает боковые стороны в точках $M$ и $N$.
а) Докажите, что $MN=PQ$.
б) Найдите площадь трапеции $ABCD$, если известно, что $AD=18$ и $BC=2$.

Задача по математике — 6832

Окружности, построенные на сторонах $AB$ и $AC$ треугольника $ABC$ как на диаметрах, пересекаются в точке $D$, отличной от $A$.
а) Докажите, что точка $D$ лежит на прямой $BC$.
б) Найдите угол $BAC$, если известно, что $angle ACB=30^$, а точка $D$ лежит на стороне $BC$, причём $DB:DC=1:3$.

Задача по математике — 6833

Окружность с центром $O$ вписана в угол, равный $60^$. Окружность большего радиуса с центром $O_$ также вписана в этот угол и проходит через точку $O$.
а) Докажите, что радиус второй окружности вдвое больше радиуса первой.
б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен $2sqrt$.

Задача по математике — 6834

Две окружности пересекаются в точках $P$ и $Q$. Прямая, проходящая через точку $P$, второй раз пересекает первую окружность в точке $A$, а вторую — в точке $D$. Прямая, проходящая через точку $Q$ параллельно $AD$, второй раз пересекает первую окружность в точке $B$, а вторую — в точке $C$.
а) Докажите, что четырёхугольник $ABCD$ — параллелограмм.
б) Найдите отношение $BP:PC$, если радиус первой окружности вдвое больше радиуса второй.

Задача по математике — 6835

Окружности с центрами $O_$ и $O_$ разных радиусов пересекаются в точках $A$ и $B$. Хорда $AC$ большей окружности пересекает меньшую окружность в точке $M$ и делится этой точкой пополам.
а) Докажите, что проекция отрезка $O_O_$ на прямую $AC$ в четыре раза меньше $AC$.
б) Найдите $O_O_$, если известно, что радиусы окружностей равны 5 и 17, а $AC=16$.

Задача по математике — 6836

На диагоналях трапеции как на диаметрах построены окружности.
а) Докажите, что их общая хорда перпендикулярна основаниям трапеции.
б) Найдите длину этой хорды, если известно, что основания трапеции равны 1 и 11, а диагонали — 6 и 8.

Задача по математике — 6837

Две равные окружности с центрами $O_$ и $O_$ пересекаются в точках $M$ и $N$. Лучи $O_M$ и $O_N$ вторично пересекают окружность с центром $O_$ в точках $A$ и $B$ соответственно, причём $M$ — середина $O_A$.
а) Докажите, что точки $A$, $B$ и $O_$ лежат на одной прямой.
б) Окружности пересекают отрезок $O_O_$ в точках $C$ и $D$. Найдите отношение отрезка $CD$ к радиусу окружностей.

🎦 Видео

Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Длина окружности. Математика 6 класс.Скачать

Задание 25 из реального ОГЭ по математике 2023 | УмскулСкачать

ЕГЭ Задание 16 Две окружностиСкачать

Геометрия Три окружности радиусов R1 = 6 см, R2 = 7 см, R3 = 8 см попарно касаются друг другаСкачать

Окружность. Как найти Радиус и ДиаметрСкачать