Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Доказательство.
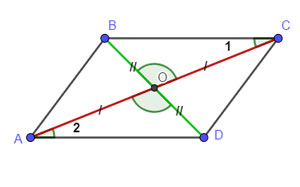
На рисунке изображён четырёхугольник ABCD, в котором диагонали АС и BD пересекаются в точке О, причём АО = OC и ВО = OD . Докажем, что четырёхугольник ABCD — параллелограмм . Так как углы ВОС и AOD равны как вертикальные и AO = OC , ВО= OD , то треугольники BOC и AOD равны по первому признаку равенства треугольников. Отсюда ВС = AD и ∠1 = ∠2 . Углы 1 и 2 являются накрест лежащими при прямых ВС и AD секущей AC . Следовательно, ВС ΙΙ AD .
Таким образом, в четырёхугольнике ABCD две противолежащие стороны равны и параллельны . Следовательно, четырёхугольник ABCD — параллелограмм.
Докажите теорему:
Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Доказательство.
На рисунке изображён четырёхугольник ABCD, в котором диагонали АС и BD пересекаются в точке О, причём АО =______и ВО =______. Докажем, что четырёхугольник ABCD —_______________________. Так как углы ВОС и______равны как ________________ и AO =_____, ВО=_____, то треугольники BOC и _______ равны по ________________признаку равенства треугольников. Отсюда ВС =____ и ∠1 = ∠___. Углы 1 и ___ являются _______________ при прямых ВС и ______ секущей____. Следовательно, ВС ΙΙ _____.
Таким образом, в четырёхугольнике ABCD две противолежащие стороны ____________ и _______________Следовательно, четырёхугольник ABCD — параллелограмм.
Видео:Признак параллелограмма (диагонали точкой пересечения делятся пополам). ЗадачаСкачать

Признаки параллелограмма
| 1 0 . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АD = ВС, АD
Доказать: АВСD — параллелограмм.
Доказательство:
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим 















3. Итак, АD


| 2 0 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АВ = DС, АD = ВC.
Доказать: АВСD — параллелограмм.
Доказательство:
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим 









3. Итак, АD = ВC, АD

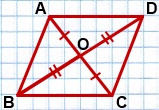
| 3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм. |
Доказательство:
Дано: АВСD — четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.
Доказать: АВСD — параллелограмм.
Доказательство:
1. Рассмотрим 








2. 





3. Итак, АD = ВC, АD

Поделись с друзьями в социальных сетях:
Видео:Диагонали параллелограмма точкой пересечения делятся пополам, теорема 8 клСкачать
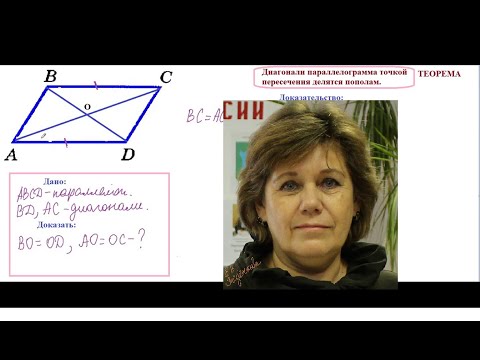
Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам
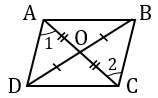
Теорема (1-й признак параллелограмма).
Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм.
AC и BD — диагонали,
Доказать : ABCD — параллелограмм.
1. Рассмотрим треугольники AOD и COB.
1) AO=OC (по условию);
2) BO=OD (по условию);
Следовательно, треугольники AOD и COB равны (по двум сторонам и углу между ними).
2. Из равенства треугольников следует равенство соответствующих углов:∠ADO=∠CBO.
А так как эти углы — внутренние накрест лежащие при прямых AD и BC и секущей BD, то AD∥BC (по признаку параллельных прямых).
3. Аналогично, ∆ AOB=∆ COD, ∠ABO=∠CDO и AB∥CD.
4. Доказали, что AD∥BC и AB∥CD.
Значит, ABCD — параллелограмм (по определению).
🎬 Видео
Геометрия Признак параллелограмма: Если в четырехугольнике диагонали точкой пересечения делятсяСкачать
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Геометрия Диагонали четырехугольника точкой пересечения делятся пополам, одна из его сторон равнаСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

8 класс, 4 урок, ПараллелограммСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 5 урок, Признаки параллелограммаСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

20 задание ОГЭ. 11429875. Анализ геометрических высказыванийСкачать

№97. Отрезки АС и BD точкой пересечения делятся пополам. Докажите, что ΔABC=ΔCDA.Скачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Алгебра - ЕНТ. 2 вариант: № 34-35.Скачать

Геометрия ОГЭ. Четырехугольники #4 (задача 9 и 11 типа ФИПИ)🔴Скачать

Четырехугольники на ЕГЭ - bezbotvyСкачать

Четырёхугольник и его элементы Геометрия 8кл Мерзляк#3Скачать

№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать