Если один из углов вписанного в окружность четырехугольника равен 63 то противоположный ему угол

Геометрия | 5 — 9 классы

Ответить верно или неверно!

1. В прямоугольном треугольнике квадрат равен разности квадратов гипотенузы и другого катета.

2. Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник — параллеограмм.

3. Площадь прямоугольника равна произведению двух его смежных сторон.

4. Вписаные углы, опирающиеся на одну и ту же хорду окружности, равны.

5. Через любые три точки проходит единственная окружность.

6. Любые два равнобедренных треугольника подобны.

7. Любые две прямые имеют не менее одной общей точки.

8. Если в четырёхугольнике две противоположные стороны равны, то этот четырёхугольник — параллеограмм.

9. Треугольник ABC, у которого AB = 4, BC = 5, AC = 6, является прямоугольным.

10. Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти окружности пересекаются.

11. Треугольник ABС — 3, BC = 4, AC = 5, является тупоугольным.

12. Диагонали параллеограмма перпендикулярны.

13. Сумма двух противоположных углов четырёхугольника равна 180градусов.

14. Сумма двух противоположных углов параллеограмма равна180градусов.

На все вопросы, кроме №5 ответил Пользователь Alfabetta

Верно : в прямоугольном треугольникеквадрат катета = разности квадратов гипотенузы и другого катета.

В трапеции две стороны параллельны.

Неверно : Черезлюбыетриточки, не принадлежащие одной прямой, проходит единственная окружность

Неверно, если прямые параллельны, то они не имеют ни одной общей точки

Неверно, в параллелограмме противоположные стороны равны и параллельны

Неверно, для прямоугольного треугольника должнавыполняться теорема Пифагора 4 ^ 2 + 5 ^ 2 = 6 ^ 2, в данном случае она не выполняется

Треугольник со сторонами 3, 4 и 5 — прямоугольный, так как выполняется теорема Пифагора 3 ^ 2 + 4 ^ 2 = 5 ^ 2, 9 + 16 = 25 — верно

Перпендикулярные диагонали у ромба и квадрата

Не во всех , а только, если 4 — угольник вписан в окружность, то сумма противолежащих углов равна 180 градусов.

В параллелограмме противоположные углы равны, а сумма двух углов, прилежащих к одной стороне равна 180 градусов.

Видео:Два угла вписанного в окружность четырехугольника равны 112 и 125Скачать

Сумма двух противоположных сторон описанного четырёхугольника равно 12 см, а радиус вписанной в него окружности равен 5 см?

Сумма двух противоположных сторон описанного четырёхугольника равно 12 см, а радиус вписанной в него окружности равен 5 см.

Найдите площадь четырёхугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

• 1)Площадь квадрата равна произведению двух его смежных сторон.

• 2)Диагональ трапеции делит её на два равных треугольника.

• 3)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

• 4)Все углы ромба равны.

• 5)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

13. Какие из следующих утверждений верны?

13. Какие из следующих утверждений верны?

1. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.

2. В любой четырёхугольник можно вписать окружность.

3. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Видео:Вписанный в окружность четырёхугольник.Скачать

ПОЖАЛУЙСТА?

Можете определить какие утверждения неверны и исправить их на верные!

Если вписанный угол равен 24°, то дуга окружности, на которую он опирается, равна 48°.

Если дуга окружности составляет 73°, то вписанный угол , опирающийся на эту дугу, равен 73°.

Если сумма двух противоположных углов прямоугольника равна 180°, около этого прямоугольника можно описать окружность.

Около любой трапеции можно описать окружность.

Если один из углов вписанного в окружность четырёхугольника равен 63°, то противоположный ему угол равен 117°.

В любой параллелограмм можно вписать окружность.

Если в четырёхугольник можно вписать окружность, сумма длин его противоположных сторон равна 24, длина третьей стороны равна 14, то длина оставшейся стороны равна 10.

Противоположные углы параллелограмма равны.

Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 40°.

Если в четырёхугольнике две стороны параллельны, то этот яетырёхугольник параллелограмм.

Если в четырёхугольнике два угла прямые, то этот четырёхугольник – параллелограмм.

Диагонали прямоугольника перпендикулярны.

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Если в четырёхугольнике диагонали равны и перпендикулярны, то этот четырёхугольник – квадрат.

Треугольник АВС, у которого АВ = 20, ВС = 21, АС = 29, является прямоугольным.

Площадь прямоугольника равна произведению двух его сторон.

Площадь треугольника равна произведению его стороны на высоту, проведённую к этой стороне.

Площадь прямоугольного треугольника равна произведению его катета на гипотенузу.

Площадь трапеции равна произведению суммы оснований на вцысоту.

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Сумма двух противоположных сторон описанного четырёхугольника и радиус вписаной в него окружности соответственно ровны 24 и 5?

Сумма двух противоположных сторон описанного четырёхугольника и радиус вписаной в него окружности соответственно ровны 24 и 5.

Найдите площадь четырёхугольника!

Должно получится 120.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1. Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник — параллелограмм.

2. Через любые три точки плоскости, не лежащие на одной прямой, проходит единственная окружность.

3. Любые два равнобедренных прямоугольных треугольника подобны.

Видео:8 класс. Четырехугольник и окружностьСкачать

Прошу помогите, пожалуйста?

Прошу помогите, пожалуйста.

Верные утверждения какие : 1)Биссектрисы треугольника пересекаются в одной точке.

2)Два треугольника подобны , если один из углов одного треугольника равен одному из углов другого треугольника.

3)Гипотенуза прямоугольного треугольника равна катету, деленному на синус угла , противолежащему этому катету.

Верное из них : 1)Медина, проведенная из вершины прямого угла, является радиусом описанной около прямоугольного треугольника окружности.

2)Существует треугольник со сторонами 7, 3, 2.

3) Площадь ромба равна произведению квадрата его стороны на на синус угла между смежными сторонами.

4) Длина окружности равна произведению числа π на радиус этой окружности.

5)Если в трапецию можно вписать окружность , то суммы ее противоположных сторон равно.

Верное из них : 1)В любой треугольник можно вписать в окружность.

2)Любые два прямоугольных треугольника подобны.

3)Центр описанной около треугольника окружности лежит в точке пересечения биссектрис углов треугольника.

4) Площадь трапеции равна сумме оснований , умноженной на высоту.

5)Любые два равносторонних треугольника подобны.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Верны утверждения или нет 1?

Верны утверждения или нет 1.

Если треугольник равнобедренный, то центр описанной окружности лежит на середине медианы 2.

Около ромба можно описать окружность 3.

Площадь параллелограмма равна произведения основания на высоту 4.

Площадь ромба равна половине произведения диагоналей 5.

Если четырёхугольник вписан в окружность, то суммы противоположных углов равны 6.

Если четырёхугольник вписан в окружность , то суммы противоположных сторон равны 7.

Площадь трапеции равна произведению полусуммы оснований на среднюю линию 8.

Площадь параллелограмма равна произведению двух его сторон на синус угла между ними 9.

В ромб нельзя вписать окружность 10.

Произведению отрезков пересекающихся хорд равны 11.

Большую длину имеет хорда, расположенная ближе к центру окружности 12.

Суммы противоположных сторон описанного четырёхугольника равны 13.

Сумы противоположных углов описанного четырёхугольника равны 14.

Синусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе 15.

Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе 16.

Синус 30 градусов больше косинуса 60 градусов 17.

Если в прямоугольном треугольнике две стороны равны 3 и 4, то третья сторона равна 5 18.

Центральный угол равен половине градусной меры дуги, на которую он опирается 19.

Вписанный угол равен половине градусной меры дуги, на которую он опирается 20.

Площадь треугольника равна половине произведению двух его сторон на синус угла между ними.

Видео:Окружность, вписанная в четырёхугольник.Скачать

Прошу помогите срочно , пожалуйста?

Прошу помогите срочно , пожалуйста.

Верные утверждения какие : 1)Биссектрисы треугольника пересекаются в одной точке.

2)Два треугольника подобны , если один из углов одного треугольника равен одному из углов другого треугольника.

3)Гипотенуза прямоугольного треугольника равна катету, деленному на синус угла , противолежащему этому катету.

Верное из них : 1)Медина, проведенная из вершины прямого угла, является радиусом описанной около прямоугольного треугольника окружности.

2)Существует треугольник со сторонами 7, 3, 2.

3) Площадь ромба равна произведению квадрата его стороны на на синус угла между смежными сторонами.

4) Длина окружности равна произведению числа π на радиус этой окружности.

5)Если в трапецию можно вписать окружность , то суммы ее противоположных сторон равно.

Верное из них : 1)В любой треугольник можно вписать в окружность.

2)Любые два прямоугольных треугольника подобны.

3)Центр описанной около треугольника окружности лежит в точке пересечения биссектрис углов треугольника.

4) Площадь трапеции равна сумме оснований , умноженной на высоту.

5)Любые два равносторонних треугольника подобны.

Видео:Вписанные углы в окружностиСкачать

Укажите номера верных ответов?

Укажите номера верных ответов.

1)Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны друг другу.

2)Если у двух равнобедренных треугольников один из углов является общим, то такие треугольники подобны.

3)Если расстояние между центрами двух окружностей меньше суммы их радиусов, то эти две окружности пересекаются.

4)Если гипотенуза и один из острых углов прямоугольного треугольника равны гипотенузе и углу другого прямоугольного треугольника, то эти прямоугольники равны.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Ответить верно или неверно?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Примеры заданий на определение верности утверждений

Скачать
презентациюУкажите номера неверных утверждений >>

Примеры заданий на определение верности утверждений. Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. Если вписанный угол равен 24, то дуга окружности, на которую опирается этот угол, равна 48. Если дуга окружности составляет 73, то вписанный угол, опирающийся на эту дугу окружности, равен 73. Центром окружности, описанной около треугольника, является точка пересечения его биссектрис. Центр окружности, описанной около прямоугольного треугольника, находится на стороне этого треугольника. Около любой трапеции можно описать окружность. Если один из углов вписанного в окружность четырехугольника равен 63, то противоположный ему угол равен 117.

Слайд 22 из презентации «Программа подготовки к ГИА по математике». Размер архива с презентацией 1122 КБ.

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Математика 9 класс

«Математика и авиация» — Математическая модель. Математика и пилот. Возникновение авиации. Карл Фридрих Гаусс. Расчеты. Система автоматического проектирования. Математика в авиации. Зарождение аэродинамики. Флаттер. Анализ и принятие решений. Ключ создания самолета. Термин «авиация». Название «математика». Природный резонанс Флаттера. Прикладная математика. Математика и авиация. Отрасли знаний.

«Программа подготовки к ГИА по математике» — Математика является одним из наиболее важных предметов школьного курса. Арифметическая прогрессия. Примеры заданий на определение верности утверждений. Структура лекций. Основные понятия и утверждения геометрии. Модуль «Реальная математика». Модуль «Алгебра». Структура ГИА по математике в 2013 году (235 минут). Окружность, описанная около треугольника. Общее количество заданий (баллов). Примеры заданий повышенного уровня.

«Математика и здоровье» — Бактерии. Пускай хорошее растёт в геометрической прогрессии. Игра «футбол». Сумма бесконечно убывающей геометрической прогрессии. Проверка ответов. Задача из сборника ГИА. Движение вперёд. Дробный член. Гигиена. Солнце. ЗОЖ. Формулы геометрической прогрессии. ЗОЖ и геометрическая прогрессия. Отдых. Веселый тест.

«Экзамен ГИА по математике» — Единая система ГИА и ЕГЭ. ГИА по математике 2012. Распределение отметок в 2010 — 2011 г. Работа территориальной экзаменационной комиссии. Документы, определяющие содержание. Основные материалы для учащихся. Итоги ГИА 2011. Учащимся в начале экзамена выдается полный текст работы. Дополнительный справочный материал. Особенности проведения государственной (итоговой) аттестации. Изменения в КИМах 2012 г.

«ГИА-9 по математике 2013» — Шкала перерасчёта суммарного балла. Интерпретация результатов экзаменационной работы по математике. Модуль «Геометрия». Модуль «Реальная математика». Распределение заданий экзаменационной работы по содержанию. Модель экзаменационной работы по математике 2013 г. Планируемые изменения КИМ ГИА для выпускников 9 класса 2013 года. Интерпретация результатов. Особенности выставления итоговой оценки. Изменения в экзаменационной работе.

Всего в теме «Математика 9 класс» 19 презентаций

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

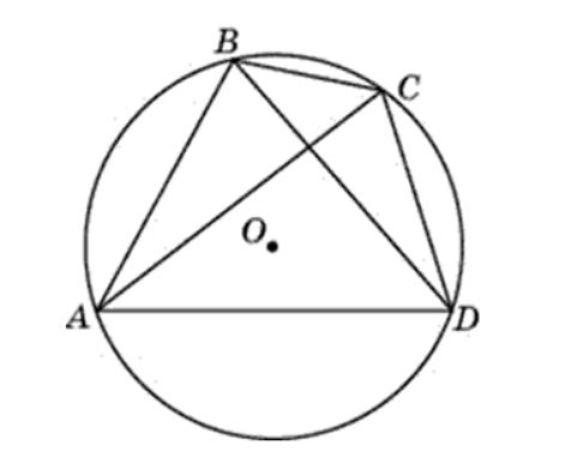
Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность

С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Общие понятия

Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.

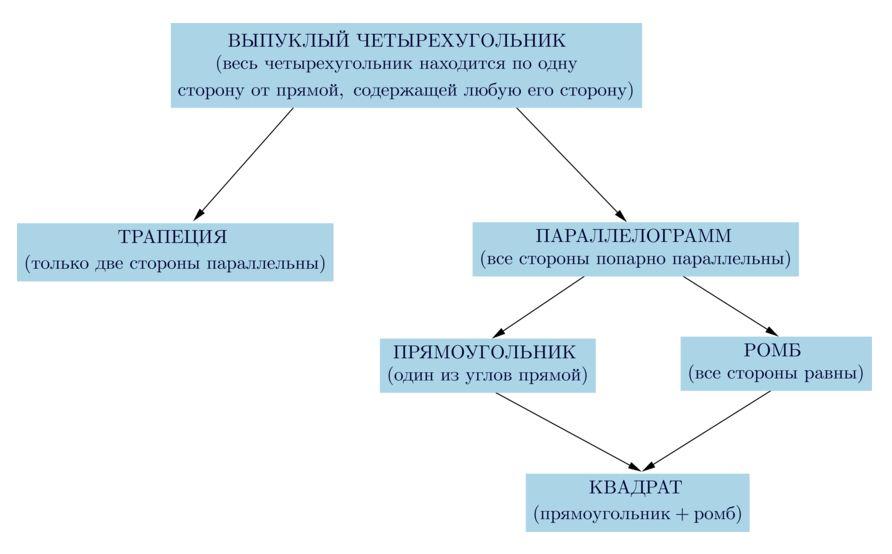
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.

Вам будет интересно: Железнодорожный техникум в Челябинске после 9 класса: специальности, отзывы

Четырехугольник может быть следующих видов:

• Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
• Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
• Прямоугольник. Фигура, у которой все 4 угла = 90º.
• Ромб. Фигура, у которой все стороны равны.
• Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.

Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.

Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.

Видео:ВЕБИНАР № 1. Планиметрия. Центральные и вписанные углы. Сумма углов вписанного четырехугольника.Скачать

Частные случаи

Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:

• Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
• Если все вершины ромба находятся на описывающей линии, то он является квадратом.
• Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.

Видео:МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать

Свойства вписанного четырехугольника в окружность

Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.

Видео:Вписанные четырехугольники. 9 класс.Скачать

Теорема 1

Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.

Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что

🎥 Видео

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать