Если диагональ четырехугольника делит его на два равнобедренных треугольника

О чем эта статья:

Видео:Геометрия Диагональ равнобокой трапеции разбивает ее на два равнобедренных треугольника. НайдитеСкачать

Определение параллелограмма

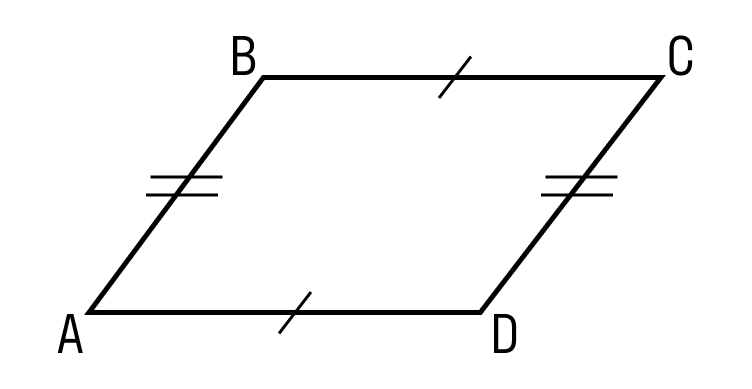
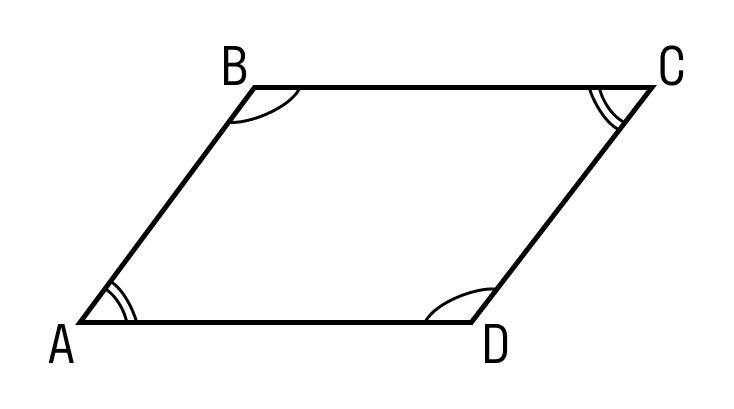
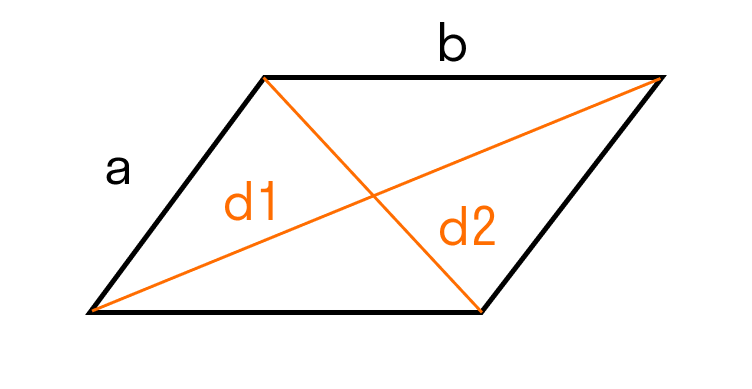
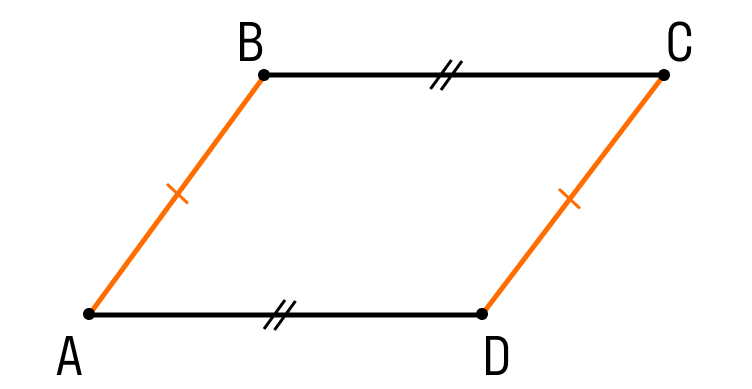
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

1. В параллелограмме точка пересечения диагоналей делит их пополам.
2. Любая диагональ параллелограмма делит его на два равных треугольника.
3. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.

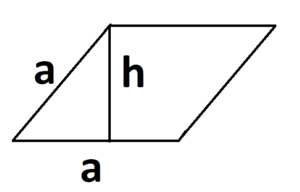
Как найти площадь параллелограмма:

1. S = a × h, где a — сторона, h — высота.
   
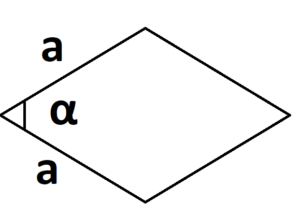
2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
   
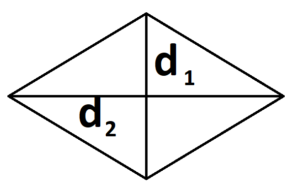
3. Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
   Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
   

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

1. Противоположные стороны параллелограмма равны.
   ABCD — параллелограмм, значит, AB = DC, BC = AD.
   
2. Противоположные углы параллелограмма равны.
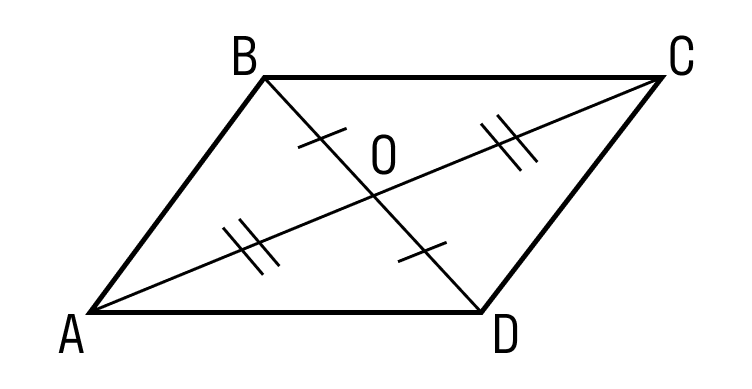
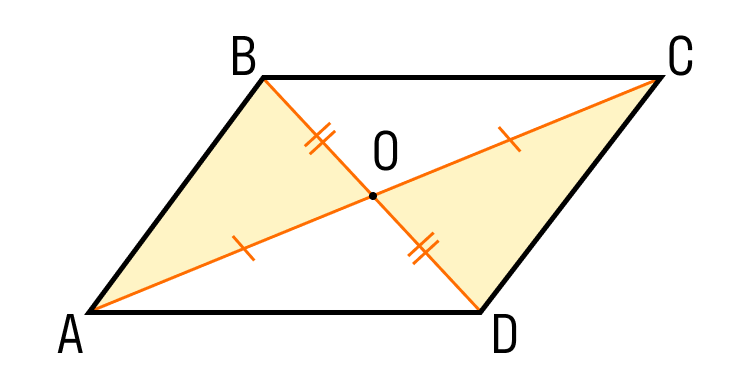
   ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
   
3. Диагонали параллелограмма точкой пересечения делятся пополам.
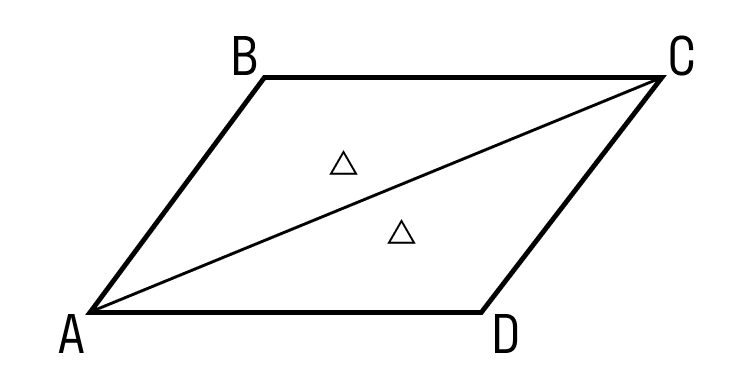
   ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
   
4. Диагональ делит параллелограмм на два равных треугольника.
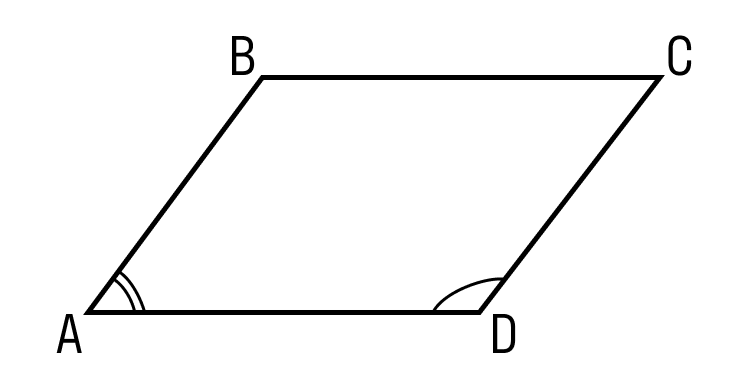
   ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
   
5. Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
   ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
   
6. В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).
   

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

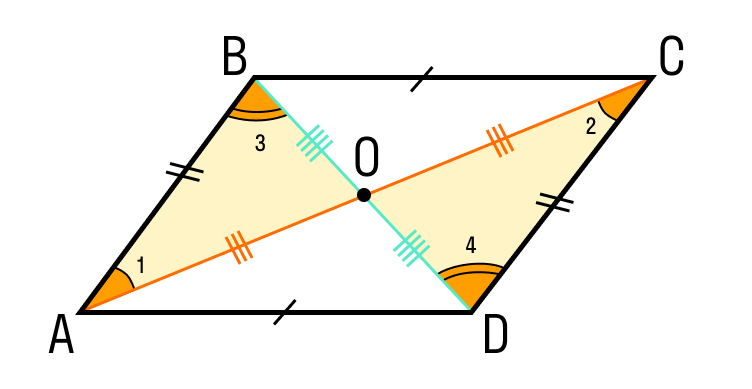
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

1. AB = CD как противоположные стороны параллелограмма.
2. ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
3. Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
   • CO = AO
   • BO = DO

   

Теорема доказана. Наше предположение верно.

Видео:Диагональ параллелограмма делит его на два равных ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

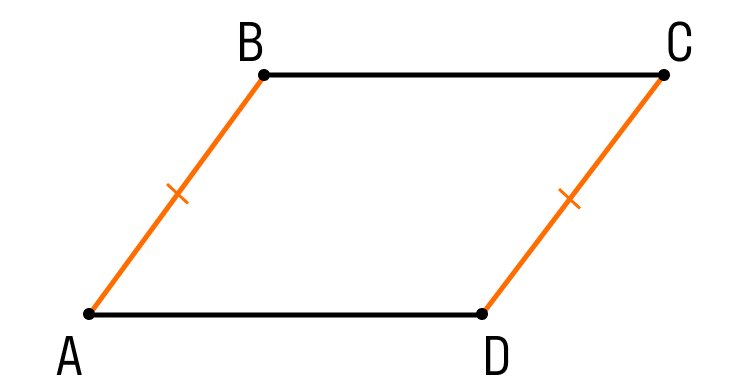
Шаг 1. Пусть в четырехугольнике ABCD:

• AB || CD
• AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

1. AC — общая сторона;
2. По условию AB = CD;
3. ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

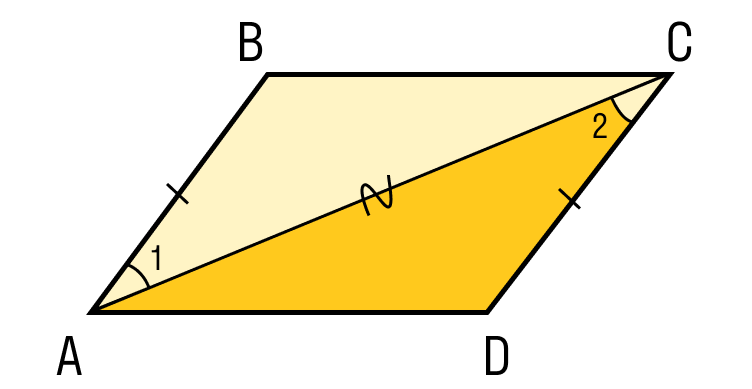
Шаг 1. Пусть в четырехугольнике ABCD:

• AB = CD
• BC = AD

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

• AC — общая сторона;
• AB = CD по условию;
• BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

• CO = OA;
• DO = BO;
• углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Если диагональ четырехугольника делит его на два равнобедренных треугольника

Первый тур ( 10 минут; каждая задача – 6 баллов ).

1.1. Известно, что а > b . Можно ли утверждать, что 9 b a ? Ответ обоснуйте.

Ответ : нет, нельзя.

Пусть, например, a = –1; b = –1,1. Тогда 10 a = –10; 9 b = –9,9, то есть 9 b > 10 a .

Отметим, что контрпримеры можно подбирать, исходя из следующих соображений. Так как a > b, то 9a > 9b. Для того, чтобы выполнялось неравенство 10а £ 9b, надо выбрать а

1.2. Диагональ четырехугольника делит его на два равнобедренных прямоугольных треугольника. Найдите все возможные значения углов этого четырехугольника.

Ответ : четыре угла по 90 ° , или два угла по 45 ° и два угла по 135 ° , или 45 ° , 135 ° и два угла по 90 ° .

Пусть диагональ BD делит четырехугольник ABCD на равнобедренные прямоугольные треугольники ABD и BCD . Возможны три случая:

1) BD – общая гипотенуза (см. рис. 1а). Тогда АВСD – квадрат, то есть все его углы – прямые.

2) BD – общий катет. Тогда либо АВСD – параллелограмм, соседние углы которого 45 ° и 135 ° (см. рис. 1б), либо точки А , С и D лежат на одной прямой (см. рис. 1в), то есть АВСD – не четырехугольник.

3) BD – катет одного треугольника и гипотенуза другого (см. рис. 1г). Тогда АВСD – прямоугольная трапеция. Ее углы, прилежащие к большей боковой стороне, равны 45 ° и 135 ° .

1.3. Может ли разность квадратов двух простых чисел быть квадратом простого числа? Ответ обоснуйте.

Ответ : нет, не может.

Предположим, что существуют такие простые числа m , n и k , что m 2 – n 2 = k 2 . Далее можно рассуждать по-разному.

Первый способ . Запишем равенство в виде: k 2 = ( m – n )( m + n ). Это означает, что число k 2 делится на каждое из чисел ( m – n ) и ( m + n ). Поскольку k – простое число, то это возможно только в том случае, если m – n = 1 и m + n = k 2 .

Существует только одна пара простых чисел, удовлетворяющих первому условию: 3 и 2. Но второму условию она не удовлетворяет, так как 5 не является квадратом натурального числа.

Второй способ . Предположим, что числа m , n и k – нечетные, тогда в левой части равенства стоит четное число, а в правой – нечетное. Поскольку существует единственное четное простое число, то n = 2 или k = 2. Тогда разность квадратов двух нечетных чисел равна 2 2 = 4, что невозможно даже в случае, если эти числа – соседние. Действительно, (2 z + 1) 2 – (2 z – 1) 2 = 8 z > 4 при любых натуральных значениях z .

Второй тур ( 15 минут; каждая задача – 7 баллов ).

2.1. Для чисел а , b и с выполняются три равенства: ( a + b )( a + b + с ) = 5, ( b + c )( b + c + a ) = 6, ( c + a )( c + a + b ) = 7. Найдите ( a + b + с ) 2 .

Сложим данные равенства почленно. Получим: ( a + b + с )( a + b + b + c + c + a ) = 18. Тогда 2( a + b + с ) 2 = 18, то есть ( a + b + с ) 2 = 9.

2.2. Точка D – середина стороны AC треугольника AB C. На стороне BC выбрана точка E так, что равны углы BEA и CED . Найдите отношение AE : DE .

Ответ : AE : DE = 2 : 1.

Первый способ . Проведем через точку D прямую, параллельную ВС , которая пересечет АЕ в точке K (см. рис. 2а). Тогда Ð EKD = Ð BEA = Ð CED = Ð EDK , следовательно, KE = DE . Так как D – середина AC , то (по теореме Фалеса) K – середина АЕ . Таким образом, AE = 2 KE = 2 DE .

Второй способ . Продлим медиану ED треугольника АЕС на ее длину: FD = ED , тогда AECF – параллелограмм (см. рис. 2б). Так как ВС || AF , то Ð EAF = Ð BEA = Ð CED = Ð EFA , значит, АЕ = FE . Следовательно, AE = 2 DE .

Третий способ . Проведем через точку D прямую, параллельную АЕ , которая пересечет ВС в точке М (см. рис. 2в). Тогда Ð EMD = Ð BEA = Ð DEM , следовательно, DE = DM . Так как D – середина AC , то (по теореме Фалеса) M – середина ЕC , то есть DM – средняя линия треугольника АСЕ . Таким образом, DE = DM = АС .

Четвертый способ . Проведем из точек D и А перпендикуляры DP и АН к стороне ВС (см. рис. 2г). Прямоугольные треугольники АНЕ и DPE подобны (по двум углам), следовательно, AE : DE = АН : DP = 2 : 1, так как DP – средняя линия треугольника АСH (по теореме Фалеса).

2.3. Цену на яблоки подняли на 20%. Однако для того, чтобы записать новую цену килограмма яблок, продавцу оказалось достаточным поменять местами цифры числа, записанного на ценнике. Сколько рублей стоили яблоки до их подорожания, если эта цена была меньше 100 рублей?

Ответ : 45 рублей.

Первый способ . Из условия задачи следует, что первоначальная цена яблок выражается двузначным числом, кратным пяти. Так как цифра единиц этого числа не может быть нулем (иначе новая цена будет начинаться с нуля) и при перестановке цифр число должно увеличиться, то достаточно проверить числа 15, 25, 35 и 45. Из этих чисел только 45 при перестановке цифр увеличивается на 20%.

Второй способ . Пусть первоначальная цена яблок – рублей за килограмм . Тогда новая цена – рублей. По условию, = 1,2 , то есть 10 b + a = 1,2(10 a + b ). Упрощая это равенство, получим, что 4 b = 5 a . Так как а и b – натуральные числа, то а = 4 , b = 5.

Третий тур ( 20 минут; каждая задача – 8 баллов ).

3.1. Известно, что m 2 + 9 mn + n 2 делится на 11 (числа m и n – целые). Докажите, что m 2 – n 2 также делится на 11.

Так как m 2 + 9 mn + n 2 делится на 11, то m 2 + 9 mn + n 2 – 11 mn = m 2 – 2 mn + n 2 = ( m – n ) 2 также делится на 11. Число 11 – простое, поэтому m – n кратно 11. Следовательно, m 2 – n 2 = ( m – n )( m + n ) также делится на 11.

3.2. На медиане ВМ треугольника АВС выбрана точка K так, что AK = BC . Луч AK пересекает сторону ВС в точке Р . Докажите, что треугольник ВКР – равнобедренный.

Первый способ . Продлим медиану ВМ на ее длину: MD = BM , тогда четырехугольник ABCD – параллелограмм (см. рис. 3а). Так как AK = BC = AD , то треугольник DAK – равнобедренный, следовательно, Ð ADK = Ð AKD . Так как Ð PBK = Ð ADK и Ð PKВ = Ð AKD , то в треугольнике ВКР Ð PBK = Ð PKВ , то есть этот треугольник – равнобедренный (с основанием BK ).

Второй способ . Продлим отрезок KM на его длину: МЕ = KM , тогда AKCE – параллелограмм (см. рис. 3б). Следовательно, СЕ = AK = CB , то есть треугольник ВСЕ – равнобедренный. Тогда Ð PBK = Ð CEB = Ð AKE = Ð BKP , значит, треугольник ВКР – равнобедренный.

3.3. В шахматном турнире каждый участник встречался с каждым один раз (победа – 1 очко, поражение – 0, ничья – пол-очка). Единоличным победителем стал Иванов. Петров сказал: «Можно удалить из турнирной таблицы любого участника и аннулировать очки, набранные во встречах с ним, и тогда единоличным победителем будет уже не Иванов, а кто-нибудь другой». Прав ли Петров? Ответ обоснуйте.

Ответ : нет, не прав.

Заметим, что при удалении одного участника из таблицы количество очков у любого из оставшихся участников не может увеличиться. Это означает, что смена единоличного победителя происходит только в том случае, когда Иванов из-за выбытия участника потерял хотя бы очко. Следовательно, у выбывшего участника Иванов выиграл.

Предположим, что Петров прав. Тогда Иванов выиграл у каждого участника турнира. Но в этом случае он останется победителем при удалении любого участника, так как все равно наберет максимальное количество возможных очков.

Полученное противоречие показывает, что Петров не прав.

Четвертый тур ( 25 минут; каждая задача – 9 баллов ).

4.1. В нескольких кошельках лежат одинаковые суммы денег. Если бы количество кошельков было на 1% меньше, а денег в каждом кошельке – на копейку больше, то общая сумма денег была бы меньше. А если бы, наоборот, количество кошельков было больше на 1%, а денег в каждом кошельке – на копейку меньше, то общая сумма денег также была бы меньше. Во сколько раз увеличится общая сумма денег, если количество кошельков не менять, но в каждый кошелек добавить по рублю?

Ответ : в 2 раза.

Первый способ («арифметический»). Из первого условия следует, что из каждой сотни кошельков убирается один, а в остальные кошельки добавляется 99 копеек. Поскольку общая сумма денег при этом становится меньше, то в каждом кошельке должно лежать больше, чем 99 копеек.

Из второго условия следует, что к каждой сотне кошельков прибавляется один, но сумма денег в этих кошельках уменьшается на 101 копейку. Поскольку общая сумма денег также уменьшится, то в каждом кошельке должно лежать меньше, чем 101 копейка.

Таким образом, в каждом кошельке лежит по 100 копеек, то есть по рублю. Если в каждый кошелек добавить еще по рублю, то количество денег в нем удвоится, значит, удвоится и общая сумма денег.

Второй способ («алгебраический»). Пусть в каждом из n кошельков находится по x копеек, тогда общая сумма денег – nx копеек. Из условия задачи следуют два неравенства: и . Из первого неравенства получим, что x > 99, а из второго – что x x x – целое, то есть x = 100.

Если в каждый кошелек добавить по рублю, то общая сумма денег станет равна n ( x + 100) копеек. При x = 100 искомое отношение равно: = 2.

4.2. Дан прямой угол О и точка С внутри него. Рассмотрим такой прямоугольник СDМЕ , что точки D и Е лежат на сторонах угла. Найдите ОМ , если диагональ прямоугольника равна 10 см, а Ð ОМС = 60 ° .

Ответ : ОМ = 5 см.

Первый способ . Пусть диагонали СМ и DE прямоугольника пересекаются в точке K (см. рис. 4а). Тогда KM = CM = 5 см, OK – медиана прямоугольного треугольника DOE , проведенная к гипотенузе, значит, OK = DE = 5 см.

Таким образом, в треугольнике OKM : KM = OK и Ð ОМK = 60 ° , поэтому этот треугольник – равносторонний. Следовательно, ОМ = KM = OK = 5 (см).

Второй способ . Рассмотрим окружность, описанную около данного прямоугольника, тогда DE – ее диаметр (см. рис. 4б). Так как угол DOE – прямой, то точка О лежит на этой окружности. Поскольку СМ – также диаметр этой окружности, то Ð СОМ = 90 ° . Таким образом, в прямоугольном треугольнике СОМ Ð ОМС = 60 ° , то есть Ð ОСМ = 30 ° . Тогда ОМ = CM = 5 (см).

4.3. Выберем произвольным образом 55 различных натуральных чисел из первой сотни. Докажите, что среди них найдутся два числа, разность между которыми равна 9.

Первый способ . Разобьем все натуральные числа первой сотни на девять групп так, чтобы внутри группы каждое число, начиная со второго, было на 9 больше предыдущего: (1, 10, …, 91, 100); (2, 11, … 83, 92); (3, 12, …, 84, 93); . ; (9, 18, . 90, 99).

Если мы выбираем числа, разность между которыми не равна 9, то из каждой группы нельзя брать числа, стоящие рядом. Так как в первой группе 12 чисел, а в остальных – по 11, то из любой группы мы сможем взять не более шести чисел, то есть всего не более 54 чисел. Добавление любого числа обязательно даст пару чисел, разность между которыми равна 9.

Второй способ . Пусть из первой сотни выбраны числа a 1 , a 2 , . a 55 . Рассмотрим эти числа вместе с числами, которые получатся, если к каждому из выбранных прибавить по 9, то есть a 1 + 9, a 2 + 9, . a 55 + 9. Получим 110 натуральных чисел, лежащих в диапазоне от 1 до 109. Следовательно ( по принципу Дирихле ), среди этих чисел найдутся хотя бы два равных числа, то есть для некоторых n и k выполняется равенство: a n + 9 = a k , что равносильно утверждению задачи.

Видео:Диагональ равнобедренной трапеции делит её на два ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Каждая диагональ четырехугольника разбивает его на два равнобедренных треугольника?

Геометрия | 5 — 9 классы

Каждая диагональ четырехугольника разбивает его на два равнобедренных треугольника.

Верно ли что этот 4угольник ромб .

Основания треугольников — диагонали, а бедра — стороны четырехугольника.

Т. к треугольники равнобедренные, т.

Е. стороны их равны, следовательно стороны четырехугольника равны, а по определению, четырехугольник, у которого все стороны равны называется ромбом.

Видео:Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

Диагональ равнобедренной трапеции разбивает её на два равнобедренных треугольника?

Диагональ равнобедренной трапеции разбивает её на два равнобедренных треугольника.

Найдите углы трапеции.

Видео:Геометрия В ромб, который делится своей диагональю на два равносторонних треугольника, вписанаСкачать

Какие из высказываний верные?

Какие из высказываний верные?

А) Диагональ параллеограмма является биссектрисой его углов.

Б) Если диагонали четырехугольника перпендикулярны, то он является ромбом.

В) В ромбе все высоты равны.

Г) Если в четырехугольнике диагональ делит его на два равных треугольника, то он является параллеограммом.

Видео:Хитрый периметрСкачать

2 ) Точка пересечения диагоналей четырехугольника является середино каждой из них ?

2 ) Точка пересечения диагоналей четырехугольника является середино каждой из них .

Как называется такой четерх угольник?

Видео:8 класс, 6 урок, ТрапецияСкачать

Равнобедренная трапеция АВСD разбивается диагональю АС на 2 равнобедренных треугольника ?

Равнобедренная трапеция АВСD разбивается диагональю АС на 2 равнобедренных треугольника .

Определить углы трапеции.

Видео:ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать

Найдите диагональ четырехугольника если его периметр равен 80 см, а периметры треугольников, на которые эта диагональ разбивае данный четырехугольник, равны 36 см и 64 см?

Найдите диагональ четырехугольника если его периметр равен 80 см, а периметры треугольников, на которые эта диагональ разбивае данный четырехугольник, равны 36 см и 64 см.

Видео:Диагонали трапеции и точка их пересеченияСкачать

Четырех угольник разделен диагональю на два треугольника?

Четырех угольник разделен диагональю на два треугольника.

Периметры этих треугольников и четырех угольника соответственно равны 30м, 34м, 36м.

Найдите длину диагонали четырехугольника.

Видео:Геометрия Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такойСкачать

Равнобедренная трапеция ABCD РАЗБИВАЕТСЯ диагональю ac на 2 равнобедренных треугольника?

Равнобедренная трапеция ABCD РАЗБИВАЕТСЯ диагональю ac на 2 равнобедренных треугольника.

Определить угры трапеции.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Является ли равносторонний треугольник равнобедренным?

Является ли равносторонний треугольник равнобедренным?

Видео:Геометрия ОГЭ. Четырехугольники #4 (задача 9 и 11 типа ФИПИ)🔴Скачать

Равнобедренная трапеция ABCD разбивается диагональю АС на 2 равнобедренных треугольника ?

Равнобедренная трапеция ABCD разбивается диагональю АС на 2 равнобедренных треугольника .

Опредилите углы трапеции.

Видео:ЕГЭ Математика Задание 6#27935Скачать

Диагональ равнобокой трапеции разбивает ее на два равнобедреных треугольника?

Диагональ равнобокой трапеции разбивает ее на два равнобедреных треугольника.

Найдите углы трапеции.

Если вам необходимо получить ответ на вопрос Каждая диагональ четырехугольника разбивает его на два равнобедренных треугольника?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

1) если диагональ биссектрисса, то параллелограмм является ромбом. Значит все четыре стороны равны, делим 34 / 4 = 8, 5 cм. Значит ВС = 7, 5см. 2) если угол 45, то треугольник будет равнобедренный и его вторая сторона тоже будет 5 см. Из большего..

4 оси имеет прчмоугольник.

Радиус основания цилиндра S1 = πR² = 16π ; R² = 16 ; R = 4 см. Сторона осевого сечения равна диаметру основания цилиндра ; равна 8 см. Площадь осевого сечения равна S2 = 8² = 64 см². Ответ : 64 см².

S поверхности шара = 4πR = 2. 5S = 4 * π *  = 4 * π * 6. 25 = 25π.

Какая фигура имеет четыре стороны одной длинны? (квадрат) перимет какой геометрической фигуры равен — (a + b)•2.

Вот вроде, думаю правильно.

Рассмотрим треугольники rsd и psd pd = rd — дано rs = ps — дано ds — общая сторона треугольники rsd и psd равны, следовательно угол pds = углу rds угол pds + угол rds = 360 — 98 = 262 (град. ) угол rds = 262 : 2 = 131 (град. ).

Ответы и решения на фото.

H = √3a / 2 r = √3a / 6 — радиус вписанной окружности R = √3a / 3 — радиус описанной окружности.

Если mh 3 см, а угол mnh 30°, то mh по свойству прямоугольного треугольника = 1 / 2 mn, значит mn 6 см отсюда mn = pq = 6 см mq = mh + hq = 5 + 3 = 8 см mq = np = 8 см находим углы hnp = 90° по свойству перпендикуляра, значит угол n получается угол m..

💡 Видео

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

11:11 или Тайна усадьбыСкачать

СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать

Геометрия Перпендикуляр, опущенный из вершины прямоугольника на его диагональ делит его угол вСкачать