Множество точек плоскости равноудаленных от центра окружности

Геометрическим множеством (ГМ) называется множество геометрических элементов (ГЭ), обладающих каким-либо общим геометрическим свойством.

5.1. Геометрические множества

Геометрические множества некоторых геометрических элементов

ГМ точек	ГМ прямых	ГМ плоскостей
1. Удаленных от заданной точки О на расстояние l
Сфера радиусом l с центром в точке О.	Совокупность прямых, касательных к сфере радиусом l с центром в точке О.	Совокупность плоскостей, касательных к сфере радиусом l с центром в точке О.
2. Удаленных от данной прямой m на расстояние l
Цилиндрическая поверхность радиусом l и осью m.	Совокупность прямых, касательных к поверхности цилиндра радиусом l и осью m, а также все образующие этой цилиндрической поверхности.	Совокупность плоскостей, касательных к поверхности цилиндра радиусом l и осью m.
3. Удаленных от данной плоскости σ на расстояние l
Две плоскости τ 1 и τ 2 //σ, расположенные по разные стороны от неё на расстоянии l
4. Равноудаленных от точек А и В
Все точки плоскости σ⊥АВ, проходящей через середину отрезка АВ.	Совокупность прямых, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.	Совокупность плоскостей, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.
5. Равноудаленных от двух параллельных прямых
Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему.	Совокупность прямых, лежащих в плоскости, проходящей через сере-дину отрезка (расстояния между данными прямыми) и перпендикулярной ему.	Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему, а также две плоскости, касательные к двум цилиндрическим поверхностям с осями – данными прямыми и равного диаметра.

5.2. Алгоритм решения задач методом геометрических множеств

1. 1. Условие задачи разбиваем на ряд простейших условий, каждому из которых должно отвечать определенное свойство искомого элемента (или элементов).

1. 1. Для каждого простейшего условия определяем удовлетворяющее ему геометрическое множество элементов.

1. 1. Находим общее решение задачи как некое геометрическое множество элементов, удовлетворяющих одновременно всем простейшим условиям. Оно представляет собой пересечение выбранных элементарных геометрических множеств.

1. Проводим анализ возможных решений, цель которого выявить когда, сколько и каких решений может быть в данной задаче в зависимости от взаимного положения заданных геометрических элементов, а, следовательно, связанных с ним геометрических множеств.

Упражнение

1. На заданной прямой m построить точку, удаленную от точки О на расстояние l (Рисунок 5.1).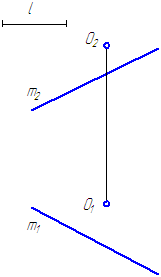

Рисунок 5.1
I. Геометрическое решение в пространстве

1. Искомые точки должны принадлежать прямой m, следовательно, решение по первому условию – любая точка на прямой.
2. Множество точек, удаленных от точки О на расстояние l образуют в пространстве сферу, с центром в точке О и радиусом равным l.
3. Общее решение задачи – точки, одновременно принадлежащие прямой m и сфере, то есть точки пересечения прямой m со сферой.

II. Графическое решение задачи (Рисунок 5.2).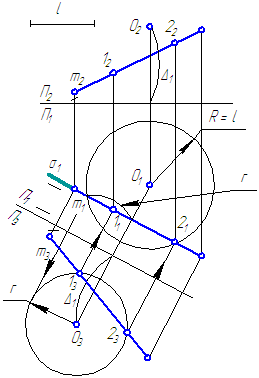

Рисунок 5.2
III. Анализ возможных решений (Рисунок 5.3).

Рисунок 5.3

Обозначим Δ – расстояние от точки О до прямой m:

• l > Δ – прямая пересечет сферу в двух точках;
• l = Δ – m – касательная к сфере → одна точка;
• l Краткая запись построения

1. 1. Строим проекцию сферы с центром в точке О и радиусом l.

1. 1. Через прямую m проводим секущую плоскость, например, σ⊥π₁. Плоскость σ пересекает сферу, в сечении – окружность.
   2. Вводим ДПП π₃⊥π₁ и π₃//σ.

1. Строим на π₃ проекции прямой m и окружности сечения, определяем точки пересечения прямой с окружностью, которые являются искомыми.

Упражнение

2. В плоскости σ=ΔАВС через точку А провести прямую AD, удаленную от точки О на расстояние l (О∈σ) (Рисунок 5.4). Геометрическое решение в пространстве

1. Прямая AD, удаленная от точки О на расстояние l, является касательной к сфере радиусом R_сф = l с центром в точке О.
2. Прямая AD∈σ.

Плоскость σ пересекает сферу по окружности.
Искомая прямая AD – касательная к окружности сечения плоскости σ и сферы.
II. Графическое решение задачи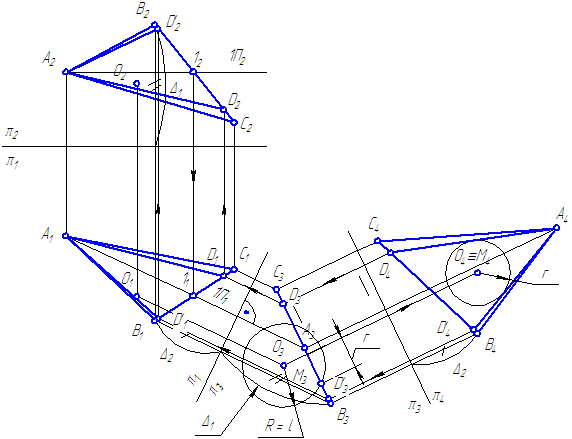

Рисунок 5.4
III. Анализ возможных решений
Обозначим Δ – расстояние от точки О до плоскости σ:

• l > Δ – плоскость пересечет сферу по окружности, → две прямые, проходящие через точку А и касательные к окружности сечения (если точка А вне окружности); если точка А на окружности сечения – одна прямая;если точка А внутри окружности сечения – решения нет;
• l = Δ – плоскость касается сферы → одна прямая, проходящая через точку А и точку касания; если точка А совпала с точкой касания → бесконечное множество прямых принадлежащих плоскости σ;
• l Краткая запись построения
  Находим истинную величину треугольника АВС, например, с помощью введения ДПП:

1. π₃⊥π₁ и π₃⊥σ.
2. π₄⊥π₃ и π₄//σ.
3. Строим окружность сечения σ со сферой. Строим касательные к этой окружности, проходящие через точку А.

5.3. Задачи для самостоятельной работы

1. Задана плоскость α=∆АВС и прямая m – общего положения. Определить угол между прямой m и плоскостью α. 2. Задана плоскость α=∆АВС и точка D вне плоскости. Повернуть точку D так, чтобы она совпала с плоскостью α. Ось вращения i⊥π₁.

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

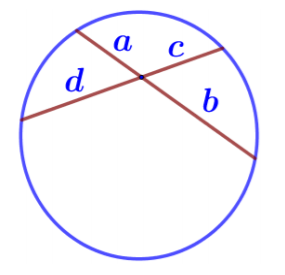
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

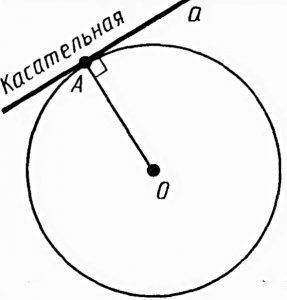
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

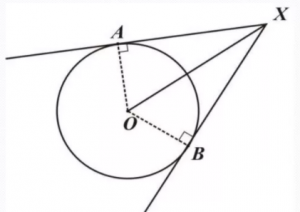
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

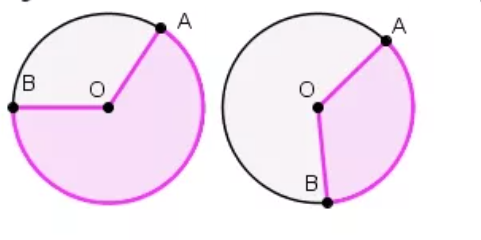
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 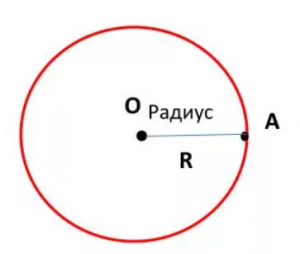Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

Свойство хорд

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Дуга, касательная, круг, сектор, сегмент

Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

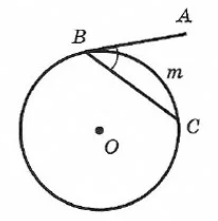
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

🎦 Видео