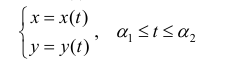Найти длину дуги кардиоиды находящейся внутри окружности (7 видео)

Уравнения кривых. Кардиоида. Улитка Паскаля.

Если применить две окружности с равными радиусами и вращать одну вокруг другой, то образуется кардиоида(греч. кардиа — сердце) — математики считают, что сформированная кривая отдаленно схожа с сердцем.

Если брать точку не на самой катящейся окружности, а внутри ее, сместив в сторону от центра, тогда будет образована кривая, получившая название Улитка Паскаля или лимакона.

Пусть a – диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус – вектора. Тогда возможны такие варианты улитки Паскаля: а > l, a = l и a 2 + у 2 +2аx) 2 – 4a 2 (х 2 + у 2 ) = 0;

в полярных координатах:

В прямоугольных координатах (параметрическая запись):

x = 2a cos t – a cos 2t;

Длина дуги одного витка кардиоиды, определяется формулой:

Площадь фигуры, ограниченной кардиоидой, определяется формулой:

Улитка Паскаля характеризуется уравнениями:

Площадь, ограниченная улиткой Паскаля:

При а > l площадь внутренней петли при вычислении по этой формуле считается дважды.

Видео:Длина дуги окружности. 9 класс.Скачать

Кардиоида

1. Уравнение. Кардиоиду можно определить как траекторию точки, лежащей на окружности круга радиуса r, который катится по окружности неподвижного круга с таким же радиусом. Она будет представлять собой, таким образом, эпициклоиду с модулем m, равным 1.

Это обстоятельство позволяет сразу же записать параметрические уравнения кардиоиды, заменяя в ранее приведенных параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:

Чтобы получить полярное уравнение кардиоиды, удобно принять за полюс точку А (рис.7), а полярную ось направить по оси абсцисс. Так как четырехугольник AOO₁M будет равнобедренной трапецией, то полярный угол точки М окажется равным углу поворота производящего круга, т. е. параметру t. Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через sin t. Сокращая полученное таким образом равенство на sin t, получим полярное уравнение кардиоиды

По виду этого уравнения

можно заключить, что кардиоида является одной из улиток Паскаля. Она может быть определена, следовательно, как конхоида круга.

Переводя уравнение (2) в прямоугольную систему координат, получим:

Из этого уравнения следует, что кардиоида является алгебраической кривой 4-го порядка.

2. Свойства. Прежде всего, поскольку кардиоида является эпициклоидой с m=1, на нее можно перенести все свойства рассмотренных нами в предыдущем параграфе эпициклоид.

Вот эти свойства и характеристики.

1. Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположную точке касания кругов, а нормаль — через точку их касания.
2. Угол , составляемый касательной к кардиоиде с радиусом-вектором точки касания, равен половине угла, образуемого этим радиусом-вектором с полярной осью.
3. Радиус кривизны в произвольной точке кардиоиды определится по формуле

4. Эволюта кардиоиды, согласно общему свойству эволют эпициклоид, будет также кардиоидой, подобной данной, с коэффициентом подобия, равным 1/3, и повернутой относительно данной на угол 180°.
5. Длина дуги кардиоиды от точки А до произвольной точки М определится по формуле

Если длину дуги отсчитывать от точки А₁, диаметрально противоположной точке А, то формула для определения длины дуги может быть записана в виде

6. Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид

7. Площадь, ограниченная кардиоидой, определится по формуле

и, как видно, равна ушестеренной площади производящего круга.

Длина всей кардиоиды определится по формуле

и, как видно, равна восьми диаметрам производящего круга. Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен

Поверхность тела, полученного от вращения кардиоиды вокруг ее оси, равняется

Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Длина дуги кривой — определение и вычисление с примерами решения

Длина дуги кривой:

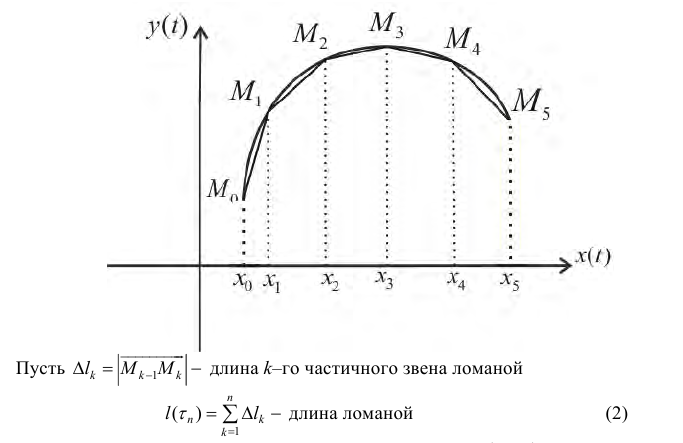
Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде

Разобьем отрезок

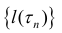
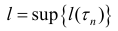
Кривая называется спрямлякмой, если множество – длин всевозможных вписанных в кривую ломаных – ограничено, при этом – называется длиной кривой L.

Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если 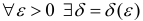такое, что ∀ разбиения диаметром Δ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.