- Ваш ответ
- решение вопроса
- Похожие вопросы
- Доказательство средней линии трапеции векторами
- Теорема о средней линии трапеции. Доказательство с помощью векторов.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Научная работа по теме «Средняя линия трапеции (несколько способов доказательств)», 8 кл.
- Скачать:
- Подписи к слайдам:
- Средняя линия трапеции. 8-й класс
- Средняя линия трапеции
- Понятие средней линии трапеции
- Теорема о средней линии трапеции
- Примеры задач на понятие средней линии трапеции
- Готовые работы на аналогичную тему
- 🔍 Видео
Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

Ваш ответ
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

решение вопроса
Видео:Теорема о средней линии трапецииСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:умножение ВЕКТОРА на число + теорема о средней линии ТРАПЕЦИИСкачать

Доказательство средней линии трапеции векторами
Видео:88. Средняя линия трапецииСкачать

Теорема о средней линии трапеции. Доказательство с помощью векторов.
Видео:Геометрия 9 класс (Урок№5 - Средняя линия трапеции.)Скачать

Ваш ответ
Видео:ТРАПЕЦИЯ теорема о средней линии Атанасян 9 классСкачать

решение вопроса
Видео:Геометрия 9 класс. Средняя линия трапецииСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,909
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Теорема о средней линии трапецииСкачать

Научная работа по теме «Средняя линия трапеции (несколько способов доказательств)», 8 кл.
Данная научная работа посвящена средней линии трапеции. Приведено 7 способов доказательств теоремы, исключая доказательство с помощью векторов, приведенное в учебнике Л.С. Атанасяна «Геометрия 7-9 классы». При доказательстве теоремы о средней линии трапеции показаны значения других теорем: теоремы о средней линии треугольника, признаков равенства треугольников, теоремы о параллельности прямых, а также следствие из аксиомы параллельных прямых, определения средней линии треугольника, признаки и определение параллелограмма, определение вертикальных углов и их свойств, свойства углов, образованных при пересечении параллельных прямых секущей. При доказательстве способа 5 доказывается единственность точки. В ходе доказательств данной теоремы использовались аналитический и синтетический методы доказательства теорем.
Видео:Средняя линия трапеции и её свойства. Векторы на плоскости. Геометрия 8-9 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Научная работа «Средняя линия трапеции (несколько способов доказательств)», 8 кл. | 2.79 МБ |
| Презентация к научной работе «Средняя линия трапеции (несколько способов доказательств)», 8 кл. | 1.41 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Подписи к слайдам:
МАТЕМАТИКА Средняя линия трапеции (несколько способов доказательства) Выполнила: Гаврилова Алиса Константиновна , обучающая 8-А кл. БОУ г. Омска «СОШ № 148» Руководитель работы: Яцюк Клавдия Васильевна , учитель математики БОУ г. Омска «СОШ № 148» ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ Г. ОМСКА бюджетное общеобразовательное учреждение города Омска «Средняя общеобразовательная школа № 148» Омск, 2012
Объект исследования: трапеция, средняя линия трапеции. Цель: показать, что доказательство теоремы о средней линии трапеции с помощью векторов, приведённое в учебнике Л.С. Атанасяна «Геометрия 7-9 классы» не является единственным, что существуют и другие способы доказательства. Задачи: Изучение научной и учебной литературы по заданной теме. Привести другие способы доказательства теоремы о средней линии трапеции. При доказательстве этой теоремы показать значение других теорем: признаков равенства треугольников, теоремы о параллельности прямых, теоремы о средней линии треугольника, а также следствие из аксиомы параллельных прямых, и определение средней линии треугольника и средней линии трапеции, признаки и определение параллелограмма. Методы исследования: применение аналитического и синтетического методов доказательства теорем.
А можно ли доказать? Теорема – математическое утверждение, истинность которого установлена путем доказательства [3]. Классическая теорема состоит из двух частей: из условия и заключения. Условие обыкновенно начинается со слова «если», а заключение со слова «то». Исходная теорема называется прямой теоремой Обратная теорема — если в исходной теореме условие сделать заключением, а заключение – условием. Если верна прямая теорема, то обратная теорема может быть неверной Взаимно обратные теоремы — если верны прямая и обратная теоремы Доказательством называется конечная последовательность формул, каждая из которых либо является аксиомой, либо получается из некоторых предыдущих формул этой последовательности по одному из правил вывода [3].
Теоретическая часть Средней линией треугольника называется отрезок, соединяющей середины двух его сторон. Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Два угла называются вертикальными , если стороны одного угла являются продолжением сторон другого. вертикальные. Прямые a и b параллельны, с –секущая. Пары углов: называются накрест лежащими. Свойство вертикальных углов . Вертикальные углы равны
Следствие 2° из аксиомы параллельных. Если две прямые параллельны третьей прямой, то они параллельны. Теорема о средней линии треугольника. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Второй признак равенства треугольников. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Признак параллельности двух прямых. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Признак параллелограмма 1° . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
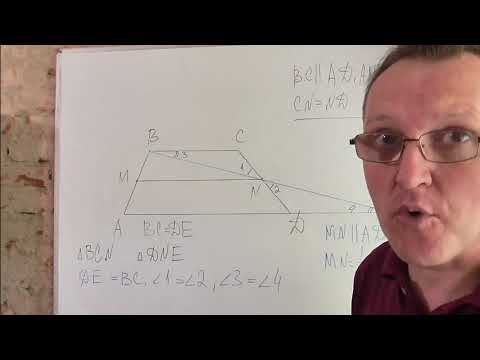
Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 1 . Доказательство . 1. Для доказательства из вершины B через точку N проведём прямую BN до пересечения этой прямой с продолжением основания AD в точке . 2. Рассмотрим ∆ BCN и (как вертикальные) (как накрест лежащие при пересечении параллельных прямых BC и А B секущей CD ); CN = ND ( по построению) 3. ∆ BCN = ( По второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам). => BC = и BN = . 4. По построению MB = AM . Значит, средняя линия трапеции MN является средней линией . По теореме о средней линии треугольника MN II => MN II AD , а AD II BC (по определению трапеции), то MN II BC ( следствие 2 из аксиомы параллельных прямых)(Если две прямые параллельны третье прямой, то они параллельны) и отрезок Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С )
Доказательство . 1. Для доказательства возьмём на основании AD точку Е . Из точки Е через точки М и N проведём прямые EM и EN до пересечения этих прямых с продолжением основания BC в точках О и Р соответственно. 2. Рассмотрим ∆BOM и ∆MAE . AM = MB (по построению); (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых OP и AD секущей АВ ) => ∆BOM = ∆MAE (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам) => OB = AE и OM = ME . Аналогично доказывается равенство треугольников PNC и DEN => PC = DE ; PN = NE . 3. Значит MN также является средней линией треугольника POE . По теореме о средней линии треугольника: MN || OP, а BC || AD (по определению трапеции). => MN || AD ( по следствию 2 из аксиомы параллельных прямых ( если две прямые параллельны третьей прямой, то они параллельны). И отрезок MN = OP = ( AD + BC ). Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 2 .
Доказательство . 1. На основании BC возьмём произвольную точку Е . Из точки Е через точки М и N проведём прямые EM и EN до пересечения этих прямых с продолжением основания AD в точках O и Р соответственно. 2. Рассмотрим ∆МВЕ и ∆АОМ . (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых ВС и ОР секущей АВ ); АМ=МВ (по построению). => ∆МВЕ =∆АОМ (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам) => ВЕ=ОА и ЕМ = ОМ . Аналогично доказывается равенство треугольников СЕ N и PND => EN = NP и EC = PD . 3. Значит MN также является средней линией треугольника POE . По теореме о средней линии треугольника MN || OP => MN || AD , а AD || BC (по определению трапеции) => MN || BC (по следствию 2 из аксиомы параллельных прямых (если две прямые параллельны третьей прямой, то они параллельны) и отрезок Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 3 .
Доказательство . 1. Для доказательства на продолжении основания А D откладываем отрезок DE=BC . Точку В соединяем с точкой Е . Прямая ВЕ проходит через точку N . В противном случае получается две середины: точки N и N 1 , а этого быть не может. 2. Рассмотрим ∆BCN и ∆DNE . BC=DE (по построению); , (как накрест лежащие углы при пересечении параллельных прямых ВС и АЕ секущими СD и ВЕ соответственно) => ∆BCN = ∆DNE по 2-му признаку равенства треугольников => CN=ND и BN=NE . 3. Рассмотрим ∆АВЕ . Т.к. BN=NE и АМ=МВ , то MN также является средней линией треугольника АВЕ . По теореме о средней линии треугольника (средняя линия треугольника параллельна одной из его сторон и равна её половине) MN || AE, => MN || AD, а AD || BC (по определению трапеции) => MN || BC (следствие 2 из аксиомы параллельных прямых) (если две прямые параллельны третьей прямой, то они параллельны) и Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 4 .
Доказательство . 1. Для доказательства на продолжении основания ВС отложим A 1 C=AD , а на AD отложим B 1 D=BC .Соединим точку А 1 с точкой В 1 . А также продолжим MN до пересечения этой прямой с прямой A 1 В 1 в точке М 1 . 2. Докажем, что точка M 1 является серединой A 1 В 1 .Соединим вершину В с В 1 и докажем, что BВ 1 проходит через точку N . Допустим, что BВ 1 проходит через точку N . Рассмотрим ∆ВСN и ∆B1ND . ; (как накрест лежащие при пересечении параллельных прямых BA 1 и АВ 1 секущими CD и ВВ 1 соответственно). ВС= B 1 D (по построению ). => ∆BCN=∆B 1 ND (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). => BN=B 1 N , CN = ND=> проходит через точку N . Рассмотрим ∆MBN и ∆M 1 B 1 N . (как вертикальные); ( как накрест лежащие углы при пересечении параллельных прямых АВ и А 1 В 1 секущей ВВ 1 ); BN= В 1 N ( по доказанному) => ∆MBN=∆M 1 В 1 N (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). => M 1 В 1 = MB . Так как AM=MB , то M 1 В 1 = AM .=> M 1 — середина стороны A 1 В 1 . Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 5 .
Доказательство продолжение . 3. Рассмотрим четырёхугольник ABA 1 В 1 . BA 1 = AВ 1 (по построению); BA 1 || AВ 1 (так как BC || AD по определению трапеции). => AB A 1 В 1 – параллелограмм. (по признаку параллелограмма 1° (если в четырёх угольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм). Рассмотрим трапецию ABCD и A 1 В 1 DC . Они равны по построению. Значит MN=M 1 N => 4. По построению AB || A 1 В 1 => AM || B 1 M 1 и M B || A 1 M 1 . Т.к. трапеции ABCD и A 1 В 1 DC равны, то => MB= M 1 B 1 и AM=A 1 M 1 ,а так как АМ=МВ и А 1 М 1 = M 1 B 1 (по построению), то АМ=МВ= A 1 M 1 = M 1 B 1 . Значит четырёхугольники МВA 1 M 1 и АМ M 1 B 1 – параллелограммы (по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм).=> BА 1 ||MM 1 и BА 1 =MM 1 ; MM 1 =AВ 1 и MM 1 || AВ 1 ( как противоположные стороны параллелограмма). => MN || BC ; BC||AD => MN || AD ( по следствию два из аксиомы параллельных прямых (если две прямые параллельны третье прямой, то они параллельны). 5. Т.к. BA 1 = MM 1 , то т.е. А т.к. BA 1 = ВС+С A 1 , а CA 1 = AD (по построению), то BA 1 =ВС+ AD . Значит Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 5 .
Доказательство . 1. Для доказательства на продолжении основания AD отложим отрезок DE = BC . А также на продолжении средней линии MN трапеции ABCD отложим отрезок NK = MN . Трапеции MBCN и KNDE будут равны (по построению). 2. Т.к. MBCN = KNDE , то КЕ=МВ , МВ=АМ => АМ=КЕ . КЕ|| MB => KE || AM . Значит по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник АМКЕ – параллелограмм. => MK = AE и MK || AE (как противоположные стороны параллелограмма) => MN || AD , а AD || BC (по определению трапеции) => MN || BC (по следствию два из аксиомы параллельных прямых)(если две прямые параллельны третьей прямой, то они параллельны). 3. Рассмотрим параллелограмм АМКЕ . MN = NK , а так как MK = MN + NK =2 MN , то Т.к. MK = AE , то А т.к. AE=AD+DE и DE=BC ( по построению ), то AE=AD+BC => , т . е . Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 6 .
Доказательство . 1. Для доказательства через точку N проведём прямую EK || AB до пересечения этой прямой с продолжением основания ВС в точке Е и с основанием AD в точке К . 2. Рассмотрим ∆NEC и ∆NKD ; CN=ND (по построению), (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых BE и AD секущей CD ). =>∆NEC=∆NKD (по второму признаку равенства треугольников( по стороне и двум прилежащим к ней углам). => CE=KD и EN=NK . 3. Рассмотрим четырёхугольник ABEK. AB || EK (по построению), BC || AD , => BE||AD (по определению трапеции) => четырёхугольник АВЕК – параллелограмм (по определению параллелограмма).=> AB=EK и AB || EK (как противоположные стороны параллелограмма). И EN=NK (из равенства треугольников NEC и NKD (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам), а AM=MB (по построению). Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 7 .
Доказательство продолжение . 4. Рассмотрим четырёхугольники MBEN и AMNK . MB = EN и MB|| EN . Значит по первому признаку параллелограмма (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник MBEN – параллелограмм. AM=NK и AM||NK => по первому признаку параллелограмма (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник AMNK – параллелограмм. => MN=BE и MN=AK ; MN||BE и MN||AK (как противоположные стороны параллелограмма) => MN|| BC и MN|| AD . 5. Т . к . MN= BE, MN=AK , то MN=BC+CE . Сложив эти равенства, получаем: AD = AK + KD , а т.к. KD = CE , то AD = AK + CE => 2 MN = AD + BC . Теорема доказана. Дано: ABCD — трапеция, MN — средняя линия трапеции. Доказать : М N II AD; MN II BC; MN = ( AD + B С ) Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 7 .
Заключение Поставленная цель достигнута. Теорема о средней линии трапеции доказана семью способами с помощью признаков равенства треугольников, теорем о параллельности прямых, теоремы о средней линии треугольника, признаков и определения параллелограмма, а также следствий из аксиомы параллельных прямых и определений средней линии треугольника, средней линии трапеции. Выше изложенные доказательства и моделирование ситуаций помогут мне при решении задач.
Литература Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов средней школы». М.: Издательство «Просвещение» 2010 г. Далингер В.А. «Методика работы над формулировкой и доказательством и закреплением теоремы». Омск. Издательство «ОмИПКРО» 1995 г. Математическая энциклопедия под редакцией И.М. Виноградова. М.: Изд. Советская Энциклопедия, 1984 г, том 4 и том 5. Погорелов А.В. «Геометрия 7-11. Учебник для 7-11 классов средней школы». М.: Издательство «Просвещение» 2010 г. Энциклопедия для детей. Том 11. Математика/ Глав. ред. М.Д. Аксенова. – М.: Аванта+, 2000 г. Якушева Г.М. «Математика. Справочник школьника». М.: Издательство «Слово» 1995 г. Якушева Г.М. «Решение задач по математике. Справочник школьника». М.: Издательство «Слово». 1996 г.
Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Средняя линия трапеции. 8-й класс
Разделы: Математика
Класс: 8
1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;
2) научить строить среднюю линию трапеции;
3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;
4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;
5) развивать логическое мышление, память, внимание.
1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:
а) определение трапеции; виды трапеций;
б) определение средней линии треугольника;
в) свойство средней линии треугольника;
г) признак средней линии треугольника.
2. Изучение нового материала.
а) На доске изображена трапеция ABCD.
б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.
Ученики изображают трапецию ABCD в тетради.
в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.
г) Далее, ребята вместе с учителем проводят аналогию между треугольником и трапецией, выясняют может ли существовать средняя линия в трапеции, и если да, то какими возможными свойствами она может обладать.
д) Записывают определение средней линии трапеции, изображая её в тетради.
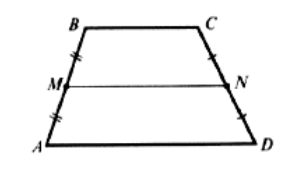
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.
Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Дано: ABCD – трапеция,
MN – средняя линия ABCD
Доказать, что:
2. MN = 
Можно выписать некоторые следствия, вытекающие из условия теоремы:
AM = MB, CN = ND, BC || AD.
На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?
Запишем дополнительное построение для одного из случаев.
Проведём прямую BN, пересекающую продолжение стороны AD в точке K.
Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия 
а) 

б) 

в) CN = ND (по следствию из условия теоремы).
Значит 

- Из равенства
BNC =
DNK следует, что BN = NK, а значит MN – средняя линия
ABK.
- MN || AD (п. 2).
- Так как ABCD – трапеция, то BC||AD, но MN || AD, значит BC || MN || AD.
- MN =
AK, но AK = AD + DK, причём DK = BC (
BNC =
DNK), значит MN =
(AD + BC).
Что и требовалось доказать.
Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).
Необходимо сказать и о других возможных способ доказательства этой теоремы:
1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.
2. Провести CF || BA и рассмотреть параллелограмм ABCF и 
3. Провести EF || BA и рассмотреть равенство 

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.
з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.
Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Средняя линия трапеции
Вы будете перенаправлены на Автор24
Видео:⏢ Полусумма оснований - средняя линия трапеции. Три доказательства. Часть 1.Скачать

Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её векторным методом.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac$.
Рассмотрим вектор $overrightarrow$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Из этого же равенства (так как $overrightarrow$ и $overrightarrow$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Видео:Трапеция. Средняя линия трапеции.Скачать
Примеры задач на понятие средней линии трапеции
Боковые стороны трапеции равны $15 см$ и $17 см$ соответственно. Периметр трапеции равен $52 см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
[15 см+17 см=32 см]
Следовательно, так как периметр равен $52 см$, сумма оснований равна
[52 см-32 см=20 см]
Значит, по теореме 1, получаем
Ответ: $10 см$.
Готовые работы на аналогичную тему
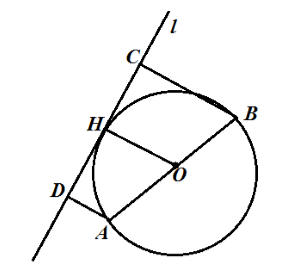
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9 см$ и $BC=5 см$. Проведем радиус $OH$ (рис. 2).
Так как $AD$ и $BC$ — расстояния до касательной, то $ADbot l$ и $BCbot l$ и так как $OH$ — радиус, то $OHbot l$, следовательно, $OH|left|ADright||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
[d=2OH=2cdot 7 см=14 см.]
Ответ: $14$ см.
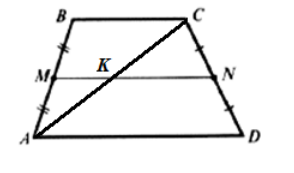
Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.
Доказательство.
Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ — точку пересечения средней линии с этой диагональю (Рис. 3).
Докажем, что $AK=KC$.
Так как $MN$ — средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ — средняя линия треугольника $ABC$. Значит $AK=KC$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 04 2021
🔍 Видео
Теорема о средней линии трапецииСкачать

Средняя линия трапеции | Геометрия 7-9 класс #84 | ИнфоурокСкачать

ТРАПЕЦИЯ. СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ. Видеоурок | ГЕОМЕТРИЯ 9 классСкачать

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ теорема класс Атанасян задачиСкачать