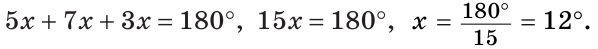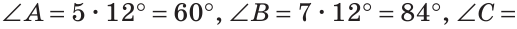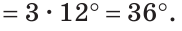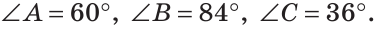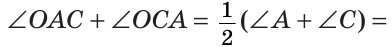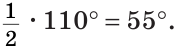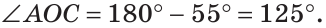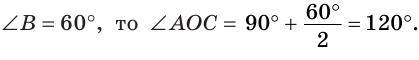- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Треугольник.
- Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
- 💥 Видео
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Сумма углов треугольника равна 180Скачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Почему сумма углов треугольника 180? #parta #Базоваяматематика #shortsСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Сумма углов треугольникаСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Почему сумма углов треугольника 180 градусов?Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:Сумма углов треугольникаСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:СУММА УГЛОВ ТРЕУГОЛЬНИКА 180 градусовСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:СУММА УГЛОВ ТРЕУГОЛЬНИКА. §16 геометрия 7 классСкачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Почему сумма углов в треугольнике равна 180? #егэ #огэ #онлайншкола #онлайнобучение #математикаСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Треугольник.
Треугольником называется геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки, образующие треугольник, называются сторонами треугольника, а их общие концы — вершинами треугольника.
Признаки равенства треугольников
- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Соотношения между сторонами и углами треугольника
- Каждая сторона треугольника меньше суммы двух других сторон.
- Сумма углов треугольника равна 180°.
- Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
- Напротив большей стороны треугольника лежит больший угол, а напротив большего угла большая сторона.
- Напротив меньшей стороны треугольника лежит меньший угол, а напротив меньшего угла меньшая сторона.
- Отношения сторон к синусу противоположных углов постоянно и равняется диаметру описанной окружности (теорема синусов).
- Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними (теорема косинусов).
- Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов (теорема тангенсов).
Площадь треугольника
Площадь треугольника через сторону 

Площадь треугольника через радиус вписанной окружности и полупериметр 
Площадь треугольника через радиус вневписанной окружности и полупериметр:
Площадь треугольника через радиусы вневписанных окружностей и радиус вписанной окружности:
Площадь треугольника через радиус описанной окружности и стороны:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через высоту и сторону:
Площадь треугольника через длины сторон и полупериметр (формула Герона):
Интересная теорема об отношении площадей треугольников, имеющих равный угол:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Замечательные точки треугольника
Инцентр треугольника — точка пересечения биссектрис треугольника. Инцентр является центром вписанной окружности.
Центроид треугольника — точка пересечения медиан треугольника.
Ортоцентр треугольник — точка пересечения прямых, содержащих высоты треугольника.
Про другие замечательные точки и прямые треугольника вы можете прочитать здесь.
Видео:Сумма углов треугольникаСкачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
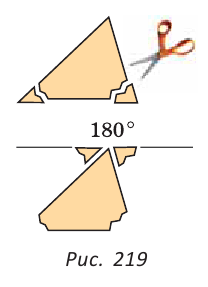
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
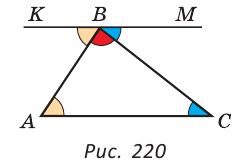
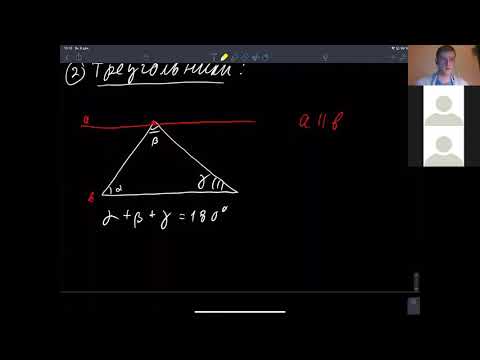
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 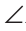
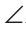
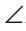
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 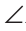
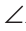
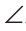





Следствия.
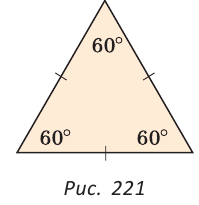
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
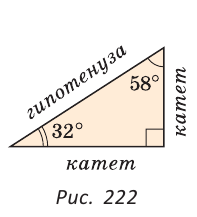
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
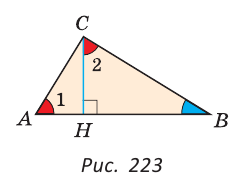
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
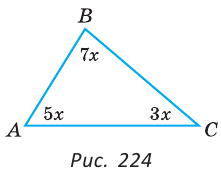
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 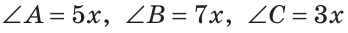
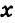
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
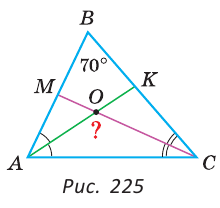
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 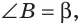
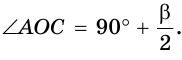
Пример:
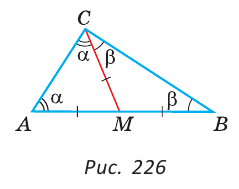
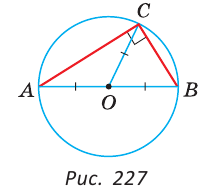
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 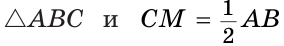
Докажем, что























Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
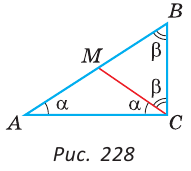
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Почему сумма углов в треугольнике равна 180°?Скачать
Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать

Почему сумма углов в треугольнике равна 180 градусовСкачать
31. Теорема о сумме углов треугольникаСкачать

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать