Видео:ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать
Решение №2085 Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
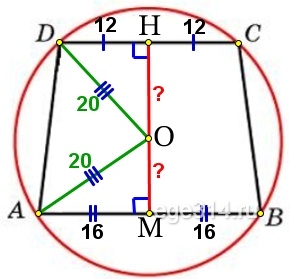
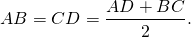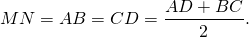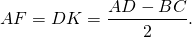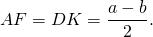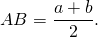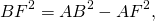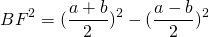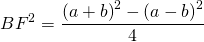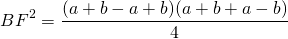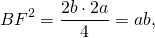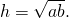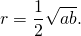Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Через центр окружности О проведём высоту НМ, она делит основания равнобедренной трапеции пополам:
DH = DC/2 = 24/2 = 12
АМ = АВ/2 = 32/2 = 16
Проведём радиусы DO и АО, получаем два прямоугольных треугольника ΔDHO и ΔAMO, найдём в них по теореме Пифагора катеты HO и МО соответственно:
Найдём высоту трапеции НМ:
НМ = НО + МО = 16 + 12 = 28
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
Тест по геометрии «Трапеция и её свойства. Площадь трапеции»
Задания рассматривают весь базовый материал темы.
Всего 14 заданий. Ответы прилагаются.
В равнобедренной трапеции синус острого угла при основании равен 0,6. Найдите периметр трапеции, если длины оснований соответственно равны 14 см и 30 см.
Основания равнобедренной трапеции равны 3 м и 8 м, угол при основании 60°. Найдите диагональ.
Меньшее основание равнобедренной трапеции равно 6 м, а большее 12 м, угол при основании 60°. Найдите радиус окружности, описанной около трапеции.
Основания трапеции равны 10 м и 31 м, а боковые стороны 20 м и 13 м. Найдите высоту трапеции.
Найдите радиус окружности, вписанной в равнобедренную трапецию, у которой сумма оснований равна 20, а разность оснований равна 12.
Диагонали трапеции АВКН пересекаются в точке О, основания ВК и АН равны соответственно 5 и 15. Площадь треугольника КОВ равна 4. Найдите площадь трапеции.
В трапеции АВМТ с основаниями АВ и МТ диагонали пересекаются в точке С, причем СМ = 2∙ АС. Площадь треугольника СМТ равна 24. Найдите площадь трапеции.
Найдите площадь равнобедренной трапеции, если ее основания равны 7 и 25, а диагональ перпендикулярна боковой стороне.
Прямоугольная трапеция с острым углом 30° описана около окружности. Площадь трапеции равна 96. Найдите большую боковую сторону трапеции.
В трапеции разность параллельных сторон равна 12, а высота равна 6. Найдите длину большего основания, если площадь трапеции равна 132.
В трапеции АВСD с основаниями АD = 2 см и ВС = 1 см, боковые стороны АВ и СD равны 1 см. Найдите квадрат диагонали трапеции.
Основания равнобокой трапеции равны 3 и 5. Найдите площадь трапеции, если ее диагонали взаимно перпендикулярны.
В прямоугольную трапецию вписана окружность радиуса 3. Найдите площадь трапеции, если ее меньшее основание равно 4.
Боковые стороны трапеции равны 9 и 12, а основания трапеции равны 30 и 15. Найдите угол, образованный продолжением боковых сторон трапеции.
Вопрос №1 — 64 см
Вопрос №2 — 7 м
Вопрос №3 — 6 м
Вопрос №4 — 12 м
Вопрос №5 — 4
Вопрос №6 — 64
Вопрос №7 — 54
Вопрос №8 — 192
Вопрос №9 — 16
Вопрос №10 — 28
Вопрос №11 — 3
Вопрос №12 — 16
Вопрос №13 — 24
Вопрос №14 — 90
Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать
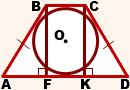
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
🔥 Видео
Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать
Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать
Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать
Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать
ОГЭ по математике. Задание 15Скачать
Задание №26 ОГЭ по математикеСкачать
СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать
Окружность вписана в равнобедренную трапецию. Теорема в задаче. Геометрия, ОГЭ, ЕГЭ. Высота и радиусСкачать
В равнобедренную трапецию, периметр которой равен 180, а площадьравна 1620, можно вписать...Скачать
Радиус описанной окружности трапецииСкачать
Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать
Задача про трапецию, описанную около окружностиСкачать
Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
Задача 6 №27439 ЕГЭ по математике. Урок 51Скачать
ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать
Почему любая вписанная трапеция будет равнобедренной? #геометрияегэСкачать
ОГЭ, ЕГЭ по математике, вписанная в трапецию окружность.Скачать
