Если четырехугольник авсд вписан в окружность то его лежат на

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

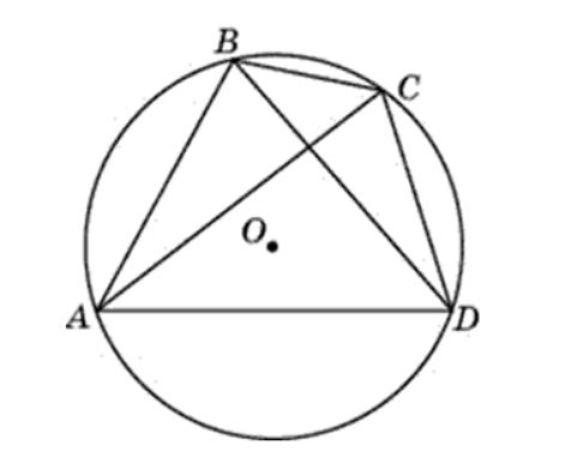
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Если четырехугольник авсд вписан в окружность то его лежат на

Четырёхугольник ABCD вписан в окружность. Точка F лежит на его стороне AD, причём прямые BF и CD параллельны, и прямые CF и AB параллельны.

а) Докажите, что отрезки BF и CF разбивают четырёхугольник ABCD на три подобных треугольника.

б) Известно, что AF = 1, DF = 4. Найдите BC.

Следовательно, треугольники BAF и FCB подобны по двум углам. Аналогично, треугольники FCB и CDF подобны по двум углам.

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б	3
Получен обоснованный ответ в пункте б имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы. Видео:Г: Четырехугольник ABCD вписан в окружность так, что сторона AD является диаметром этой окружностиСкачать Общие понятия Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки. Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры. Вам будет интересно: Железнодорожный техникум в Челябинске после 9 класса: специальности, отзывы Четырехугольник может быть следующих видов: Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами. Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет. Прямоугольник. Фигура, у которой все 4 угла = 90º. Ромб. Фигура, у которой все стороны равны. Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые. Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º. Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника. Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать Частные случаи Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи: Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник. Если все вершины ромба находятся на описывающей линии, то он является квадратом. Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре. Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать Свойства вписанного четырехугольника в окружность Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример. Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать Теорема 1 Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º. Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что 📸 Видео 11 класс, 43 урок, Вписанный четырехугольникСкачать Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать №17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать Решение задания №16 варианта 1 из ОГЭ по математике Ященко 36 вариантов ФИПИ 2023 Ответы ГДЗСкачать 2128 в четырёхугольник ABCD вписана окружность AB = 7 BC = 12 CD = 9Скачать 3 правила для вписанного четырехугольника #shortsСкачать Вписанный в окружность четырёхугольник.Скачать Всё про углы в окружности. Геометрия | МатематикаСкачать Поделиться или сохранить к себе: Смотрите также Является ли четырехугольник прямоугольником если все его углы равны все его стороны равны Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 градусам Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 degree180 Является ли четырехугольник параллелограммом если его противоположные углы равны да или нет Чья комната походила как будто на сарай имела неправильный вид четырехугольника Что можно сказать о четырехугольнике если серединные перпендикуляры пересекаются в одной точке Четырехугольники авсд и дсеф имеют общую сторону сд точки а д ф Четырехугольник является правильным если все его стороны равны и один из углов