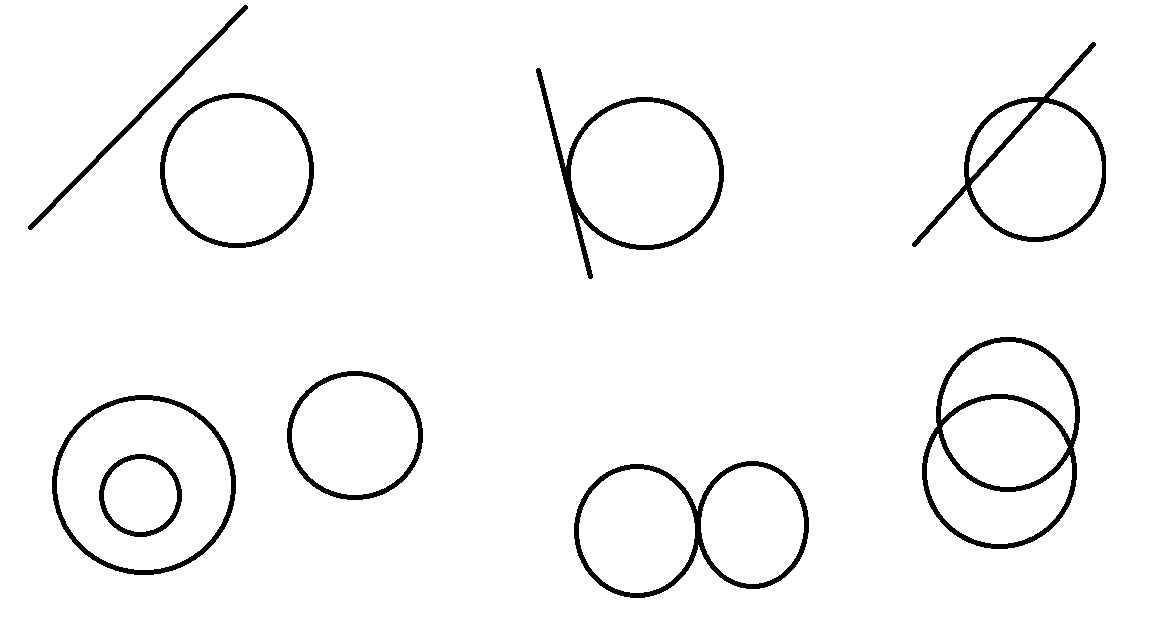Сколько точек пересечения у окружности (7 видео)

Пересечение двух окружностей

Этот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют

Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности.

Формулы для расчета приведены под калькулятором.

Содержание

Точки пересечения двух окружностей
Первая окружность
Вторая окружность
Пересечение окружностей
Всё про окружность и круг
Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей?
Чему равно максимальное количество точек пересечения двух прямыми двух окружностей ?
Какие окружности пересекаются?
Сколько точек может оказаться в пересечении : двух окружностей?
Сколько точек может оказаться в пересечении1)прямой и окружности2)двух окружностей?
Сколько точек может оказаться в пересечении 1)прямой и окружности 2)двух окружностей?
Сколько точек пересечения имеют прямая х + у = 6 и окружность (х — 2) ^ 2 + ( у — 1) ^ 2 = 9?
Сколько точек пересечения имеют окружность и прямая?
Сколько точек пересечения могут иметь прямая и окружность?
Какое наибольшое количество общих точек может быть при пересечении окружности с прямоугольником?
Сколько точек пересечения могут иметь прямая окружностью?
🎦 Видео

Точки пересечения двух окружностей

Первая окружность

Вторая окружность

Видео:Определение точки пересечения окружности с прямойСкачать

Пересечение окружностей

Сама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2.

При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):

Случай	Описание	Условие
Тривиальный случай — окружности совпадают (это одна и та же окружность)
Окружности не касаются друг друга	r1 + r2″ />
Одна окружность содержится внутри другой и не касается ее
Окружности пересекаются в двух точках	Не выполнено ни одно из условий выше
Окружности соприкасаются в одной точке	Частный случай предыдущего

Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже:

Сначала калькулятор находит отрезок a

Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде):

И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения:
Первая точка:

Обратите внимание на разные знаки перед вторым слагаемым

По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей?

Математика | 5 — 9 классы

Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей.

А) варианты ответа 0 — если прямая и окружность не пересекаются ; 1 — если прямая является касательной к окружности 2 — если прямая пересекает окружность

б) 0 — если окружности не имеют точек пересечения 1 — окружности пересечены в одной касательной точке 2 — окружности пересекаются бесконечное число точек пересечения если одна окружность имеет наложение на другую с одинаковым диаметром.

Наглядно ответы представил в приложении.

Видео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Чему равно максимальное количество точек пересечения двух прямыми двух окружностей ?

Видео:Теорема о числе точек пересечения окружности и прямойСкачать

Какие окружности пересекаются?

Запиши под каждым рисунком число точек пересечения.

Видео:Алгоритмы. Пересечение окружностейСкачать

Сколько точек может оказаться в пересечении : двух окружностей?

Видео:Взаимное расположение и точки пересечения прямой и окружностиСкачать

Сколько точек может оказаться в пересечении1)прямой и окружности2)двух окружностей?

Сколько точек может оказаться в пересечении

1)прямой и окружности

Видео:Пересечение двух окружностейСкачать

Сколько точек может оказаться в пересечении 1)прямой и окружности 2)двух окружностей?

Сколько точек может оказаться в пересечении 1)прямой и окружности 2)двух окружностей.

Видео:Теорема о числе точек пересечения окружности с прямой и окружностьюСкачать

Сколько точек пересечения имеют прямая х + у = 6 и окружность (х — 2) ^ 2 + ( у — 1) ^ 2 = 9?

Сколько точек пересечения имеют прямая х + у = 6 и окружность (х — 2) ^ 2 + ( у — 1) ^ 2 = 9.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Сколько точек пересечения имеют окружность и прямая?

Сколько точек пересечения имеют окружность и прямая.

Видео:Пересечение двух окружностейСкачать

Сколько точек пересечения могут иметь прямая и окружность?

Видео:Построение окружности по трём точкам.Скачать

Какое наибольшое количество общих точек может быть при пересечении окружности с прямоугольником?

Видео:Нахождение точки, лежащей на окружностиСкачать

Сколько точек пересечения могут иметь прямая окружностью?

Объясни с помощью черчежа.

На этой странице находится вопрос Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.