Доказать параллельность плоскостей abc и a1b1c1 дано abcd пространственный четырехугольник da1

— подготовка к контрольной работе.

Дано: ABCD — параллелограмм, АА1 и СС1. Прямые АА1 и СС1 не лежат в одной плоскости параллелограмма (рис. 1).

Доказать: (А1АВ) || (C1CD).

Решение: АВ || CD — противоположные стороны параллелограмма, АА1 || СС1 по условию. BA ∩ AA1 = A, DC ∩ СС1 = С. По признаку параллельности плоскостей (А1АВ) || (C1CD). Что и требовалось доказать.

Дано: (рис. 2).

а) Доказать: А1В1 || А2В2.

а) Из определения параллельных прямых в пространстве следует, что прямые а и b лежат в одной плоскости, которая пересекает параллельные плоскости α и β по прямым А1В1 и А2В2. По 1° свойству параллельных плоскостей А1В1 || А2В2. Что и требовалось доказать.

б) Отрезки А1А2 || В1В2, так как α || β по условию. А1В1 || А2В2 по выше доказанному. Значит, А2В2В1А1 — параллелограмм по определению. По свойству параллелограмма (сумма углов, прилежащих к одной стороне, равна 180°) Так как по условию (Ответ: ∠A2A1B1 = 40°.)

Дано: ABCD — параллелограмм. Прямые АА1 и СС1 не лежат в плоскости параллелограмма АА1 || СС1 (рис. 3).

Доказать: (A1AD) || (С1СВ).

Решение: ВС || AD — противоположные стороны параллелограмма. СС1 || АА1 по условию; По признаку параллельности двух плоскостей (A1AD) || (С1СВ). Что и требовалось доказать.

Дано: (рис. 4).

а) Доказать: А1В1 = А2В2.

а) Отрезки А1А2 и B1В2 параллельных прямых а и b параллельны, то есть А1А2 || B1B2. а || Р, α || β по условию. Следовательно, по свойству 2° параллельных плоскостей А1А2 = В1В2. Значит, противоположные стороны А1А2 и В1В2 четырехугольника А2В2В1А1 равны и параллельны и А2В2В1А1 — параллелограмм. В параллелограмме противолежащие стороны равны, поэтому А1В1 = A2В2, что и требовалось доказать.

б) В параллелограмме противоположные углы равны, ∠B1A1A2 = ∠B1B2A2, так как ∠B1A1A2 = 50°, то ∠B1B2A2 = 50°. (Ответ: ∠B1B2A2 = 50°.)

Дано: ABCD и A1B1CD параллелограммы не лежат в одной плоскости (рис. 5).

Доказать: (ADA1) || (ВСВ1).

противоположные стороны параллелограммов AD ∩ DA = D; В1С ∩ СВ = С. По признаку параллельности двух плоскостей (ADA1) || (ВСВ1).

Дано: (рис. 6).

Доказать: a) АВ || CD; б) ∠ADC четырехугольника ABCD равен 65°.

Найти остальные углы.

Решение: Прямые АС и BD пересекаются и задают плоскость ABCD. По свойству параллельных плоскостей (п. 11, 1°) АВ || CD, ΔAОВ = ΔDOC по второму признаку как внутренние накрест лежащие при параллельных АВ и DC и секущей BD и АС для второй пары. АВ = DC по условию.

Из равенства треугольников следует, что OB = OD, АО = СО, то есть диагонали четырехугольника делятся точкой пересечения пополам. Значит, ABCD — параллелограмм. У параллелограмма противоположные углы равны. Если ∠ADC = 65 °, то ∠ABC = 65 °, ∠DAB = 180° — ∠ADC = 180° — 65° = 115°. ∠BCD = ∠DAB = 115°. (Ответ: 65°, 115°, 115°.)

Дано: ABCD и ABC1D1 — параллелограммы не лежат в одной плоскости (рис. 7).

Доказать: (СВС1) || (DAD1).

Решение: по определению параллелограмма Имеем две пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся прямым другой плоскости. Следовательно, по признаку параллельности двух плоскостей (СВС1) || (DAD1). Что и требовалось доказать.

Дето: D = О, АВ = CD, ∠BAD = 130° (рис. 8).

а) Доказать: AD || ВС.

б) Найти: ∠ABC, ∠ADC, ∠BCD.

а) Две пересекающиеся прямые единственным образом задают плоскость. Отрезки АС и BD пересекаются и задают плоскость ABCD, которая пересекает параллельные плоскости аир по прямым АВ и DC. По свойству 1° параллельных плоскостей АВ || DC. АВ = DC по условию.

Поэтому четырехугольник ABCD — параллелограмм. Значит, AD || ВС. Что и требовалось доказать.

б) В параллелограмме сумма углов, прилежащих к одной стороне равна 180°. В параллелограмме противоположные углы равны. ∠BAD = ∠BCD, ∠ABC = ∠ADC. Так как ∠BAD = 130°, то ∠BCD = 130°, ∠ADC = 50°, то и ∠ABC = 50°. (Ответ: ∠BCD = 130°, ∠ADC = 50°, ∠ABC = 50°.)

Дано: (рис. 9).

При каком взаимном расположении прямых а и b α || β?

Решение: α || β, если прямые а и b пересекаются.

Две пересекающиеся прямые единственным образом задают плоскость. Прямые а и b пересекаются и задают плоскость γ. Пересекающиеся прямые а и b плоскости γ параллельны плоскости α. Значит, α || γ (задача 51). Рассуждая аналогично, имеем β || γ, α || γ, α || у. Следовательно, α || β (задача 60).

Дано: α || β. Отрезки АС и BD пересекаются в точке О, (рис. 10).

а) При каком дополнительном условии пересечения отрезков ABCD — прямоугольник?

б) Доказать: ABCD — равнобокая трапеция.

а) Две пересекающиеся прямые единственным образом задают плоскость.

Отрезки АС и BD пересекаются и задают плоскость ABCD. По 1° свойству параллельных плоскостей АВ || CD. По условию АС = BD. При дополнительном условии, что пересекающиеся отрезки делятся точкой пересечения пополам, ABCD будет являться прямоугольником.

б) Из выше доказанного АВ || CD. Значит, ABCD — трапеция по определению. AC || BD — ее диагонали. Если диагонали трапеции равны, то она равнобедренная. АС = BD по условию.

Значит, ABCD — равнобокая трапеция.

Дано: (рис. 11).

При каком взаимном расположении прямых а и b α || β?

Решение: и а и b скрещивающиеся прямые; если прямые а и b скрещивающиеся или параллельные.

Дано: (рис. 12).

а) При каком дополнительном условии пересечения отрезков ABCD — квадрат?

б) Доказать, что ABCD трапеция, в которой высота равна средней линии.

а) По свойству 1° параллельных АВ || DC. При условии, что отрезки точкой пересечения делятся пополам, ABCD будет являться квадратом.

б) ΔBDC = ΔADC (по двум сторонам и угу между ними. DC — общая, AD = BC, ∠ADC = ∠BCD как углы при основании равнобедренной трапеции).

Из равенства треугольников следует, что ∠BDC = ∠ACD. Тогда DO = ОС. ΔDOC — прямоугольный и равнобедренный. ОМ — высота,, биссектриса, медиана. ΔОМС — прямоугольный равнобедренный. ОМ = МС или ОМ = 1/2DC.

Аналогично где MN — высота, 1/2(DC + ВА) — средняя линия трапеции.

Примечание: Задачи решаются учащимися самостоятельно. Уровень выбирают ученики. Анализ решений делает учитель.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

Видео:№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

Решение задач по теме «Параллельность прямых и плоскостей»

Урок 14. Решение задач по теме «Параллельность прямых и плоскостей»

Цели урока: повторить теорию; подготовить учащихся к контрольной работе.

I. Организационный момент. II . Актуализация знаний учащихся. 1. Проверка домашнего задания. а) первый ученик у доски решает № 45 (а); б) второй ученик у доски решает № 46; в) третий ученик у доски решает № 90.

№ 45 а. Дано: ABCD — параллелограмм; а || ВС; а ∉ ( ABCD ) (рис. 1). Доказать: а и CD — скрещивающиеся. Найти: угол между а и CD , если ∠ BCD = 50°.

I . 1) Так как а || ВС, то проведем через них плоскость α.

2) D ∉ α, так как иначе DC ∈ α, то есть α совпала бы с плоскостью ABCD и а ∈ ( ABCD ), что противоречит условию.

3) Тогда DC ∩ α в точке С ∉ а;

4) Вывод: по теореме а и CD — скрещивающиеся.

II . Проведем через точку С прямую, параллельную прямой а. Это будет прямая СВ. Значит, угол между а к СВ равен углу между прямыми СВ и CD , то есть ∠ BCD = 50°. (Ответ: 50°.)

№ 47. Дано: ABCD — пространственный четырехугольник; АВ = CD , N — середина AD ; М — середина ВС (рис. 2). Доказать: угол между АВ и MN и угол между CD и MN равны.

1. Точка К — середина АС. Через точку М проведем МК || АВ, МК — средняя линия Δ ABC , ∠( MN , АВ) = ∠ KMN .

2. МК — средняя линия Δ ABC , МК || АВ; МК = 1/2АВ. Через точку N проведем NK || DC , NK — средняя линия Δ ADC , ∠( DC , MN ) = ∠ MNK .

3. NK — средняя линия Δ CDP ; NK || CD ; NK = 1/2 CD .

4. КМ = 1/2АВ, NK = 1/2 DC , так как АВ = DC , то КМ = NK , то есть Δ NMK — равнобедренный.

5. Вывод: ∠ KMN = ∠ MNK , что и требовалось доказать.

а) Решение: Если АВ ∈ α и АВ || DC , то DC || α;

б) Решение: АВ не параллельно CD . Так как АВ и CD лежат в одной плоскости ABCD , то АВ ∩ CD . Значит, CD пересекает плоскость α.

2. Работа по карточкам (см. приложение). Три ученика работают по карточкам. Остальные учащиеся решают задачу по планиметрии.

Дано: ABCD — трапеция, описанная около окружности. АВ = CD . Т, М, Р, Е — точки касания окружности. ВТ = 2, АЕ = 8 (рис. 4). Найти: SABCD .

Решение задач к карточкам.

а) Так как К — середина АВ, и М — середина ВС, то КМ — средняя линия ΔАВС. КМ || АС и КМ = 1/2АС. Так как ACFE — квадрат, то EF || АС.

б) Так как ACFE — квадрат, то

(Ответ: а) КМ || EF ; б) КМ = 4 см.)

№ 2. Дано: ABCD — трапеция: BC || AD — основания. AD ∈ α; точка Е — середина АВ; точка F середина CD ; EF ∉ α (рис. 5). Доказать: EF || α.

1. Так как Е — середина АВ, F — середина CD , то EF — средняя линия трапеции ABCD . EF || AD — по свойству средней линии.

2. AD ∈ α — по условию.

3. Вывод: EF || α (по признаку параллельности прямой и плоскости, п. 6, стр. 12).

№ 3. Дано: точки А, В, С, и D не лежат в одной плоскости (рис. 6).

Найти: а) прямую, скрещивающуюся с АВ; б) прямую, скрещивающуюся с ВС.

( Ответ : a) DC; б ) AD.)

№ 1. Дано: А, В, С, D — не лежат в одной плоскости; точка Е — середина АВ; точка F — середина ВС; точка М — середина DC ; точка К — середина AD (рис. 7).

а) Доказать: EFMK — параллелограмм.

б) Найти: P ( EFMK ), если АС = 6 см; BD = 8 см.

а) КМ — средняя линия Δ ADC ⇒ КМ || АС; КМ = 1/2АС; MF — средняя линия Δ DCB ⇒ MF || BD ; MF = 1/2 BD ; EF — средняя линия Δ ABC ⇒ EF || AC ; EF = 1/2 AC ; KE — средняя линия Δ ABD ⇒ KE || BD ; KE = 1/2 BD . Значит,

Вывод: EFMK — параллелограмм.

б) или (Ответ: a ) EFMK — параллелограмм; б) P ( EFMK ) = 14 см.)

№ 2. Дано: α — плоскость; точка (рис. 8).

Доказательство: Пусть b ∉ α, но b проходит через точку A ∈ α, ⇒ b ∩ α в точке А. А так как a || α, то получается, что b ∩ α, что противоречит условию. Значит, прямая b ∈ α, что и требовалось доказать. (Ответ: b ∈ α.)

№ 3. Дано: ABCDA 1 B 1 C 1 D 1 — куб (рис. 9).

Укажите: три прямые, проходящие: а) через точку D и скрещивающиеся с прямой АВ1; б) через точку B 1 и скрещивающиеся с прямой A 1 D 1.

а) прямая АВ1 ∈ ( AA 1 B 1 B ); прямые DD 1, DC и DB — скрещивающиеся с прямой АВ1, так как они не лежат в плоскости (АА1В1В);

б) прямая A 1 D ∈ ( AA 1 D 1 D ); прямые B 1 D 1, В1С1 и ВВ1 — скрещивающиеся с прямой A 1 D , так как они не лежат в плоскости ( AA 1 D 1 D ). (Ответ: a ) DD 1, DC , DB ; б) B 1 D 1; В1С1; ВВ1.)

№ 1. Дано: ( ABC ) — плоскость; точка M ∉ ( ABC ); точка D — точка пересечения медиан ΔМАВ; точка Е — точка пересечения медиан ΔМВС (рис. 10).

а) Доказать: ADEC — трапеция.

б) Найти: DE , если АС = 12 см.

а) Рассмотрим ΔАКС и Δ DEK . У них

а) (по свойству медиан в треугольниках); б) ∠ K — общий. Значит, ΔАКС и Δ DEK подобны по двум сторонам и углу между ними.

Из этого следует, и они являются соответственными при прямых DE и АС и секущих АК и СК.

Вывод: DE || АС, значит, ADEC — трапеция.

б) Так как ΔА KC

Δ DKE с коэффициентом подобия k = 1/3, то (Ответ: a ) ADEC — трапеция; б) DE = 4 см.)

№ 2. Дано: АА1, ВВ1, СС1 — отрезки, не лежащие в одной плоскости. АА1 ∩ ВВ1 ∩ СС1 в точке О. Точка О — их середина (рис. 11).

Доказать: прямая АВ || (А1СВ1).

Доказательство: Рассмотрим плоскость, проходящую через отрезки АА1 и ВВ1 (такая есть и единственная, так как АА1 ∩ ВВ1 в точке О).

В этой плоскости лежит четырехугольник АВА1В1, диагонали которого точкой пересечения О делятся пополам. Значит, АВА1В1 — параллелограмм. Следовательно, АВ || А1В1, а А1В1 прямая, которая лежит в плоскости А1СВ1, следовательно, АВ || (А1СВ1). (Ответ: АВ || (А1СВ1).)

Выслушивается и проверяется решение домашних задач.

III. Решение задач (фронтальная работа).

Дополнительные задачи, № 88 стр. 32.

Дано: AC || BD — прямые; АС ∩ α в точке А; DB ∩ α в точке В; точки С и D лежат по одну сторону от α; АС = 8 см, BD = 6 см, АВ = 4 см (рис. 12).

Доказать: CD ∩ α в точке Е.

1. Проведем плоскость через прямые АС и BD . Если CD || АВ, то ABCD — параллелограмм, значит АС = BD , но АС = 8 см, BD = 6 см. Значит CD не параллельна АВ, но так как они лежат в одной плоскости, то CD ∩ АВ в точке Е, то есть CD ∩ α в точке Е.

2. а) как соответственные при AC || BD и секущих АЕ и СЕ.

ΔЕСА (по трем углам) ⇒ (Ответ: 12 см.)

Дополнительные задачи, № 97 стр. 32 (рис. 13 а, б, в).

Решение: Рассмотрим ∠АВС и ∠А1В1С1, у которых АВ || А1В1 и ВС || В1С1. Проведем прямую ВВ1.

а) тогда ∠АВС = ∠А1В1С1 (см. п. 8) (рис. 13 а).

б) тогда рассмотрим ∠АВ C 2 — смежный к ∠АВС ⇒ (по теореме пункта 7) ∠АВС2 = ∠ А1В1С1, значит, (рис. 13 б).

в) тогда рассмотрим ∠А2ВС2 — вертикальный к ∠АВС. Следовательно, (см. рис. 13 в).

№ 87 б. Дано: ABCDA 1 B 1 C 1 D 1 — параллелепипед. (рис. 14).

Построить: MNK — сечение.

Построение: Возможны два случая:

I . 1) Соединим точки К и М, КМ || ВС;

3) Соединим К с А и M c D ;

4) AKMD — искомое сечение.

II. 1) КМ ∩ ВС в точке L ;

2) Через точку N проведем прямую а || КМ;

3) а ∩ АА1 в точке Р;

4) Соединим точу К и точку Р;

5) NL ∩ DC в точке К;

6) KPNRM — искомое сечение.

IV. Подведение итогов урока. V. Домашнее задание: п. 1-9. № 87 (а), 46, 93, вопросы № 9-16 (стр. 31-32).

Видео:№98. В треугольниках ABC и A1B1C1 AB = А1В1, АС = А1С1, ∠A=∠A1 На сторонах AB и A1B1 отмеченыСкачать

Презентация по математике на тему «Решение задач. Пространственный четырехугольник»

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:№127. В треугольниках ABC и А1В1С1 АВ=А1В1, ВС=В1С1, ∠B =∠B1Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Пространственый четырехугольник. Решение задач. гимназия 64 учитель математики Котельникова Н. В.

Доказательство Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно. Нужно доказать, что MNKL – параллелограмм. Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине. Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине. И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых. Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.

Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости. № 1.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 975 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 337 человек из 71 региона

Ищем педагогов в команду «Инфоурок»

• Котельникова Наталья ВячеславовнаНаписать 4680 07.01.2019

Номер материала: ДБ-345782

07.01.2019 235

07.01.2019 135

07.01.2019 169

07.01.2019 216

07.01.2019 245

05.01.2019 83

30.12.2018 404

29.12.2018 174

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

10 класс, 10 урок, Параллельные плоскостиСкачать

№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

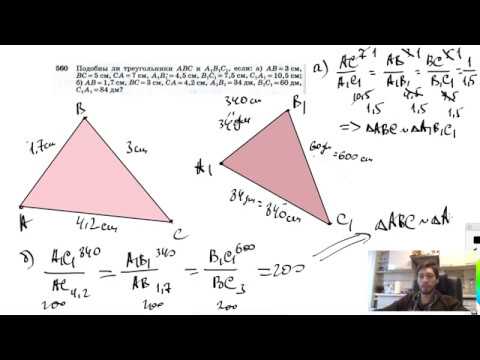
№560. Подобны ли треугольники ABC и A1B1C1, если: а) АВ = 3 см, ВС=5 см, СА=7 см, А1В1=4,5см,Скачать

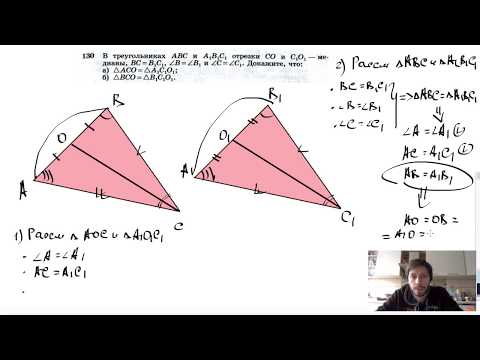
№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать

10. Параллельные плоскостиСкачать

№19. Стороны АВ и ВС параллелограмма ABCD пересекают плоскость αСкачать

№63. Параллельные плоскости a и β пересекают сторону АВ угла ВАС соответственно в точках A1 и A2Скачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

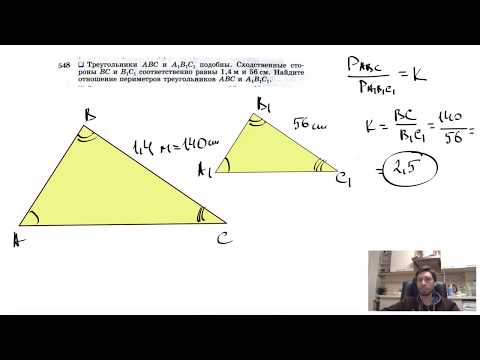
№548. Треугольники ABC и А1В1С1 подобны. Сходственные стороны ВС и В1С1 соответственно равныСкачать

№545. Треугольники ABC и А1В1С1 подобны, и их сходственные стороны относятся как 6:5Скачать