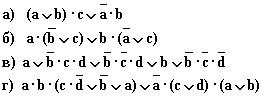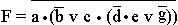Рассмотрим, например, теорему «если четырехугольник является прямоугольником, то в нем диагонали равны». Построим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это ложное высказывание, в чем легко убедиться (в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником).
Рассмотрим теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Это истинное предложение и потому является теоремой. Ее называют теоремой, обратной данной.
Для любой теоремы вида А


В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Для всякой теоремы вида А


Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность: ( А


Эту равносильность называют законом контрапозиции.
Теоремы А



1. В следующих теоремах выделим условие и заключение: а) «Для того чтобы разность двух чисел делилась на 2, достаточно, чтобы на 2 делилось уменьшаемое и вычитаемое»;
б) «Для того чтобы четырехугольник был квадратом, необходимо, чтобы хоты бы один из его углов был прямым».
Решение: а) Слово достаточно относится к предложению «уменьшаемое и вычитаемое делится на 2», следовательно, это предложение и является условием теоремы. Тогда заключение теоремы – «разность двух чисел делится на 2».
б) В данной теореме есть слово «необходимо», которое относится к предложению «чтобы четырехугольник был квадратом». Значит, это и будет условием данной теоремы. А ее заключением в таком случае будет предложение «один из углов четырехугольника прямой».
2. Сформулируем следующие теоремы в виде «если …, то …»:
а) «Перпендикуляр к одной из двух параллельных прямых также перпендикуляр к другой»; б) «Всякий параллелограмм имеет центр симметрии».
Решение: а) Выделим условие и заключение теоремы: «Перпендикуляр к одной из двух параллельных прямых» – условие, «перпендикуляр к другой» – заключение. Тогда теорема примет вид: «Если есть перпендикуляр к одной из двух параллельных прямых, то он является также перпендикуляром к другой прямой».
б) Условие теоремы – «всякий параллелограмм», заключение – «имеет центр симметрии». Нашу теорему тогда можно переформулировать следующим образом: «Если фигура параллелограмм, то она имеет центр симметрии».
3. Дана теорема: «Если в четырехугольнике две противоположные стороны равны и параллельны, то четырехугольник параллелограмм». Сформулируем предложения, являющиеся обратным, противоположным и обратно противоположным.
Решение: Выделим условие и заключение данной теоремы. Условие: «в четырехугольнике две противоположные стороны равны и параллельны». Заключение: «четырехугольник – параллелограмм».
Поменяв местами условие и заключение, получим теорему, обратную данной: «Если четырехугольник – параллелограмм, то две противоположные стороны равны и параллельны», так как данное предложение истинно.
Заменяя условие и заключение исходной теоремы их отрицаниями, получим теорему, противоположную данной: «Если в четырехугольнике две противоположные стороны не равны или не параллельны, то четырехугольник – не параллелограмм». Это предложение также истинно.
Меняя местами отрицание условия и отрицание заключения, получим истинное предложение, которое является обратно противоположной теоремой: «Если четырехугольник – не параллелограмм, то две противоположные стороны не равны или не параллельны».
Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

III. Решение логических задач с помощью рассуждений
Не являются отрицаниями друг друга: а), в), е), ж), з), и).
5.6. Определите значения истинности высказываний:
- а) “наличия аттестата о среднем образовании достаточно для поступления в институт”;
- б) “наличие аттестата о среднем образовании необходимо для поступления в институт”;
- в) “если целое число делится на 6, то оно делится на 3”;
- г) “подобие треугольников является необходимым условием их равенства”;
- д) “подобие треугольников является необходимым и достаточным условием их равенства”;
- е) “треугольники подобны только в случае их равенства”;
- ж) “треугольники равны только в случае их подобия”;
- з) “равенство треугольников является достаточным условием их подобия”;
- и) “для того, чтобы треугольники были неравны, достаточно, чтобы они были неподобны”;
- к) “для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны”.
Ложны: а), д), е), ж).
5.7. Подставьте в приведённые ниже высказывательные формы вместо логических переменных a, b, c, d такие высказывания, чтобы полученные таким образом составные высказывания имели смысл в повседневной жизни:
Нет ответа
5.8. Формализуйте следующий вывод: «Если a и b истинны, то c — истинно. Но c — ложно: значит, a или b ложны».

5.9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: “Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги”.
Формализуйте также ответ сына: “Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди”.
Решение. Введем обозначения для логических высказываний: а – “ты будешь говорить правду”; b – “тебя возненавидят люди”; c – “тебя возненавидят боги”. Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так:

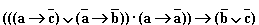
5.10. Пусть a = “это утро ясное”, а b = “это утро теплое”. Выразите следующие формулы на обычном языке:
| а) “это утро ясное и тёплое”; | ж) “это утро не ясное или не тёплое”; |
| б) “это утро ясное и оно не тёплое”; | з) “это утро не ясное и не тёплое”; |
| в) “это утро не ясное и оно не тёплое”; | и) “это утро ясное или не тёплое”; |
| г) “это утро не ясное или оно тёплое”; | к) “если это тро ясное, то оно не тёплое”; |
| д) “это утро ясное или оно не тёплое”; | л) “если это утро не ясное, то оно тёплое”; |
| е) “это утро не ясное или оно не тёплое”; | м) “это утро ясное и не тёплое”. |
5.11. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:
- а) истинно тогда и только тогда, когда оба данных выказывания ложны;
- б) ложно тогда и только тогда, когда оба данных высказывания истинны.
а) 

5.12. Из трех данных высказываний a, b, c постройте составное высказывание, которое истинно, когда истинно какое-либо одно из данных высказываний, и только в этом случае.
Ответ: 
5.13. Определите с помощью таблиц истинности, какие из следующих формул являются тождественно истинными или тождественно ложными:
а) 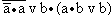 | д)  |
б)  | е)  |
в) 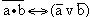 | ж)  |
г) 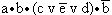 |
Тождественно истинные: а), в), е);
тождественно ложные: г), д), ж).
5.14. Упростите следующие формулы, используя законы склеивания:
- а)
- б)
- в)
- г)
- д)
Решение:.
а) b•c; б) a; в) c•(a v b) v a•b (Указание: повторить четвертое логическое слагаемое 3 раза); г) a v c.
5.15. Упростите следующие формулы, используя законы поглощения:
- а)
- б)
- в)
- г)
5.16. Постройте таблицы истинности для логических формул и упростите формулы, используя законы алгебры логики:
- а)
- б)
- в)
- г)
- д)
- е)
- ж)
- з)
- и)
- к)
а) a v c; б) 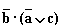





5.17. Приведите примеры переключательных схем, содержащих хотя бы два переключателя, функция проводимости которых
- а) тождественно равна единице;
- б) тождественно равна нулю.
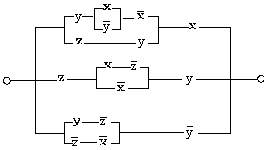
5.18. Найдите функции проводимости следующих переключательных схем:
| а) |  | б) | 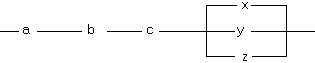 |
| в) |  | г) |  |
5.19. Проверьте равносильность следующих переключательных схем:
- а)
- б)
- в)
- г)
д)
5.20. Постройте переключательные схемы с заданными функциями проводимости:
5.21. Упростите функции проводимости и постройте переключательные схемы, соответствующие упрощенным функциям:
а)
б)
в)
г)
д)
е)
ж)
з)
и) 
5.22. Упростите следующие переключательные схемы:
- а)
- б)
- в)
- г)
ЛОГИЧЕСКИЕ ЗАДАЧИ
5.23. Три девочки — Роза, Маргарита и Анюта представили на конкурс цветоводов корзины выращенных ими роз, маргариток и анютиных глазок. Девочка, вырастившая маргаритки, обратила внимание Розы на то, что ни у одной из девочек имя не совпадает с названием любимых цветов.
Какие цветы вырастила каждая из девочек?
Аня вырастила маргаритки, Роза – анютины глазки, Маргарита – розы.
5.24. Виновник ночного дорожно-транспортного происшествия скрылся с места аварии.
Первый из опрошенных свидетелей сказал работникам ГАИ, что это были “Жигули”, первая цифра номера машины — единица.
Второй свидетель сказал, что машина была марки “Москвич”, а номер начинался с семёрки.
Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы.
При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера.
Какой марки была машина и с какой цифры начинался номер?
“Жигули”, номер начинается с семерки.
5.25. Пятеро одноклассников: Ирена, Тимур, Камилла, Эльдар и Залим стали победителями олимпиад школьников по физике, математике, информатике, литературе и географии.
Известно, что:
- победитель олимпиады по информатике учит Ирену и Тимура работе на компьютере;
- Камилла и Эльдар тоже заинтересовались информатикой;
- Тимур всегда побаивался физики;
- Камилла, Тимур и победитель олимпиады по литературе занимаются плаванием;
- Тимур и Камилла поздравили победителя олимпиады по математике;
- Ирена cожалеет о том, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
Ирена – победитель олимпиады по математике, Тимур – по географии, Камилла – по физике, Эльдар – по литературе, Залим – по информатике.
5.26. Ирена любит мороженое с фруктами. В кафе был выбор из таких вариантов:
- пломбир с орехами;
- пломбир с бананами;
- пломбир с черникой;
- шоколадное с черникой;
- шоколадное с клубникой.
В четырёх вариантах Ирене не нравились или тип мороженого, или наполнитель, а в одном варианте ей не нравились ни мороженое, ни наполнитель. Она попросила приготовить из имеющихся продуктов порцию по своему вкусу.
Какое же мороженое и с какими фруктами любит Ирена?
Пломбир с клубникой. Пояснение. Два других возможных варианта – шоколадное с орехами и шоколадное с бананами, не подходят по условию задачи (число вариантов, в которых не нравятся и тип мороженого и наполнитель, в этих случаях равно двум вместо одного).
5.27. На очередном этапе автогонок “Формула 1” первые четыре места заняли Шумахер, Алези, Хилл и Кулхардт. Опоздавший к месту награждения телерепортёр успел заснять пилотов, занявших второе и третье места, которые поливали друг друга шампанским. В это время Шумахер с четвёртым гонщиком пожимали друг другу руки. Далее в кадр попал мокрый Хилл, поздравляющий пилота, занявшего второе место. Напоследок оператор снял сцену, в которой Шумахер и Кулхардт пытались втащить на пьедестал почёта пилота, занявшего четвёртое место.
Просматривая отснятый материал, режиссёр спортивного выпуска быстро разобрался, кто из пилотов какое место занял. Он знал, что, в соответствии с церемонией награждения победителей гонок, пилоты, занявшие первые три места, поливают друг друга шампанским из огромных бутылок знаменитой фирмы — спонсора соревнований.
Какое же место занял каждый пилот?
Шумахер пришел первым, Кулхардт – вторым, Хилл – третьим и Алези – четвертым. Пояснение. Шумахер не четвертый, так как он пожимал четвертому руку; он не второй и не третий, так как пилоты, занявшие эти места поливали друг друга шампанским в то время как он пожимал руку. Следовательно, Шумахер первый. Далее, раз Хилл мокрый, то он занял одно из призовых мест, но не первое и не второе (поздравлял пилота, занявшего второе место). Следовательно, Хилл – третий. Кулхардт занял не четвертое место, так как он втаскивал на пьедестал пилота, занявшего четвертое место. Следовательно, он второй.
5.28. В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырёх богатырей погубить Змея, а награду за то обещал великую. Вернулись богатыри с победой и спрашивает их царь: “Так кто же из вас главный победитель, кому достанется царёва дочь и полцарства?”
Засмущались добры молодцы и ответы дали туманные:
Сказал Илья Муромец: “Это все Алеша Попович, царь-батюшка”.
Алеша Попович возразил: “То был Микула Селянинович”.
Микула Селянинович: “Не прав Алеша, не я это”.
Добрыня Никитич: “И не я, батюшка”.
Подвернулась тут баба Яга и говорит царю: “А прав то лишь один из богатырей, видела я всю битву своими глазами”.
Кто же из богатырей победил Змея Горыныча?
Добрыня Никитич.
5.29. При составлении расписания на пятницу были высказаны пожелания, чтобы информатика была первым или вторым уроком, физика — первым или третьим, история — вторым или третьим.
Можно ли удовлетворить одновременно все высказанные пожелания?
Есть две возможности:
а) первый урок – информатика, второй – история, третий – физика;
б) первый урок – физика, второй – информатика, третий – история.
5.30. Обсуждая конструкцию нового трёхмоторного самолёта, трое конструкторов поочередно высказали следующие предположения:
1) при отказе второго двигателя надо приземляться, а при отказе третьего можно продолжать полёт;
2) при отказе первого двигателя лететь можно, или при отказе третьего двигателя лететь нельзя;
3) при отказе третьего двигателя лететь можно, но при отказе хотя бы одного из остальных надо садиться.
Лётные испытания подтвердили правоту каждого из конструкторов. Определите, при отказе какого из двигателей нельзя продолжать полёт.
При отказе второго двигателя нельзя продолжать полет.
5.31. В соревнованиях по плаванию участвовали Андрей, Виктор, Саша и Дима. Их друзья высказали предположения о возможных победителях:
1) первым будет Саша, Виктор будет вторым;
2) вторым будет Саша, Дима будет третьим;
3) Андрей будет вторым, Дима будет четвёртым.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно.
Какое место на соревнованиях занял каждый из юношей, если все они заняли разные места.
Первое место занял Саша, второе – Андрей, третье – Дима, четвертое – Виктор.
5.32. Для длительной международной экспедиции на околоземной космической станции надо из восьми претендентов отобрать шесть специалистов: по аэронавтике, космонавигации, биомеханике, энергетике, медицине и астрофизике. Условия полёта не позволяют совмещать работы по разным специальностям, хотя некоторые претенденты владеют двумя специальностями. Обязанности аэронавта могут выполнять Геррети и Нам; космонавигатора — Кларк и Фриш; биомеханика — Фриш и Нам; энергетика — Депардье и Леонов; врача — Депардье и Хорхес; астрофизика — Волков и Леонов.
По особенностям психологической совместимости врачи рекомендуют совместные полеты Фриша и Кларка, а также Леонова с Хорхесом и Депардье. Напротив, нежелательно, чтобы Депардье оказался в одной экспедиции с Намом, а Волков — с Кларком.
Кого следует включить в состав экспедиции?
В экспедицию следует включить: аэронавтом – Геррети, космонавигатором – Кларка, биомехаником – Фриша, энергетиком – Депардье, врачом – Хорхеса, астрофизиком – Леонова.
Пример 3. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов «альт» и «кларнет» заполним нулями:
| скрипка | флейта | альт | кларнет | гобой | труба |
| Браун | |||||
| Смит | |||||
| Вессон |
Из таблицы видно, что на трубе может играть только Вессон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки «Вессон» можно заполнить нулями:
| скрипка | флейта | альт | кларнет | гобой | труба |
| Браун | |||||
| Смит | |||||
| Вессон |
Из таблицы видно, что играть на флейте и на гобое может только Смит.
| скрипка | флейта | альт | кларнет | гобой | труба |
| Браун | |||||
| Смит | |||||
| Вессон |
Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
Пример 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
| Имя | Юра |
| Профессия | врач |
| Увлечение | туризм |
Буква «а», присутствующая в слове «врач», указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы «т» и «р», встречающиеся в слове «туризм», следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы «ю» и «р». Следовательно, окончательно имеем:
| Имя | Юра | Тимур | Влад |
| Профессия | физик | врач | юрист |
| Увлечение | бег | туризм | регби |
Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
Пример 5. Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда, тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
1. Джуди живет не в Париже, а Линда — не в Риме;
2. парижанка не снимается в кино;
3. та, кто живет в Риме, певица;
4. Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
Решение. Составим таблицу и отразим в ней условия 1 и 4, заполнив клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание:
| Париж | Рим | Чикаго | Пение | Балет | Кино |
| Джуди | |||||
| Айрис | |||||
| Линда |
Далее рассуждаем следующим образом. Так как Линда живет не в Риме, то, согласно условию 3, она не певица. В клетку, соответствующую строке «Линда» и столбцу «Пение», ставим 0.
Из таблицы сразу видно, что Линда киноактриса, а Джуди и Айрис не снимаются в кино.
| Париж | Рим | Чикаго | Пение | Балет | Кино |
| Джуди | |||||
| Айрис | |||||
| Линда |
Согласно условию 2, парижанка не снимается в кино, следовательно, Линда живет не в Париже. Но она живет и не в Риме. Следовательно, Линда живет в Чикаго. Так как Линда и Джуди живут не в Париже, там живет Айрис. Джуди живет в Риме и, согласно условию 3, является певицей. А так как Линда киноактриса, то Айрис балерина.
В результате постепенного заполнения получаем следующую таблицу:
| Париж | Рим | Чикаго | Пение | Балет | Кино |
| Джуди | |||||
| Айрис | |||||
| Линда |
Ответ. Айрис балерина. Она живет в Париже.
III. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Пример 6. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Пример 7. В поездке пятеро друзей — Антон, Борис, Вадим, Дима и Гриша, знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:
Дима сказал: «Моя фамилия — Мишин, а фамилия Бориса — Хохлов». Антон сказал: «Мишин — это моя фамилия, а фамилия Вадима — Белкин». Борис сказал: «Фамилия Вадима — Тихонов, а моя фамилия — Мишин». Вадим сказал: «Моя фамилия — Белкин, а фамилия Гриши — Чехов». Гриша сказал: «Да, моя фамилия Чехов, а фамилия Антона — Тихонов».
Какую фамилию носит каждый из друзей?
Решение. Обозначим высказывательную форму «юноша по имени А носит фамилию Б» как АБ, где буквы А и Б соответствуют начальным буквам имени и фамилии.
Зафиксируем высказывания каждого из друзей:
Допустим сначала, что истинно ДМ. Но, если истинно ДМ, то у Антона и у Бориса должны быть другие фамилии, значит АМ и БМ ложно. Но если АМ и БМ ложны, то должны быть истинны ВБ и ВТ, но ВБ и ВТ одновременно истинными быть не могут.
Значит остается другой случай: истинно БХ. Этот случай приводит к цепочке умозаключений:
БХ истинно 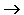
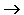
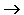
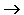
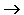
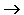
Ответ: Борис — Хохлов, Вадим — Тихонов, Гриша — Чехов, Антон — Мишин, Дима — Белкин.
Пример 8.Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:
Россия — «Проект не наш, проект не США»;
США — «Проект не России, проект Китая»;
Китай — «Проект не наш, проект России».
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду.
Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.
Решение. Для удобства записи пронумеруем высказывания дипломатов:
Россия — «Проект не наш» (1), «Проект не США» (2);
США — «Проект не России» (3), «Проект Китая» (4);
Китай — «Проект не наш» (5), «Проект России» (6).
Узнаем, кто из министров самый откровенный.
Если это российский министр, то из справедливости (1) и (2) следует, что победил китайский проект. Но тогда оба утверждения министра США тоже справедливы, чего не может быть по условию.
Если самый откровенный — министр США, то тогда вновь получаем, что победил китайский проект, значит оба утверждения российского министра тоже верны, чего не может быть по условию.
Получается, что наиболее откровенным был китайский министр. Действительно, из того, что (5) и (6) справедливы, cледует, что победил российский проект. А тогда получается, что из двух утверждений российского министра первое ложно, а второе верно. Оба же утверждения министра США неверны.
Ответ: Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США.
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

5.14. Упражнения
5.1. Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
- а) «Солнце есть спутник Земли«;
- б) «2+3=4«;
- в) «сегодня отличная погода«;
- г) «в романе Л.Н. Толстого «Война и мир» 3 432 536 слов«;
- д) «Санкт-Петербург расположен на Неве«;
- е) «музыка Баха слишком сложна«;
- ж) «первая космическая скорость равна 7.8 км/сек«;
- з) «железо — металл«;
- и) «если один угол в треугольнике прямой, то треугольник будет тупоугольным«;
- к) «если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный«.
[ Ответ ] 5.1. Являются высказываниями: а), г), д), ж), з), и), к);
не являются высказываниями: б); в); е).
5.2. Укажите, какие из высказываний предыдущего упражнения истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
[ Ответ ] 5.2. Истинные: д), з), к);
ложные: а), и);
истинность трудно установить: г);
можно рассматривать и как истинное, и как ложное в зависимости от требуемой точности представления: ж).
5.3. Приведите примеры истинных и ложных высказываний:
- а) из арифметики; б) из физики;
- в) из биологии; г) из информатики;
- д) из геометрии; е) из жизни.
[ Ответ ] 5.3. Образцы.
Истинные высказывания: а) «2+2=4«; б) «сила притяжения тел обратно пропорциональна квадрату расстояния между ними» в) «зайцы питаются растениями»; г) «бит — фундаментальная единица информации, используемая в теории информации»; д) «два треугольника равны, если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника»; е) «понедельник — первый день недели».
Ложные высказывания: а) «4+3=5»; б) «тело падает на Землю с ускорением, пропорциональным своей массе»; в) «животные это неживая природа» г) «информатика — наука о термической обработке металлов»; д) «квадрат это фигура у которой пять сторон»; е) «лев — домашнее животное»
5.4. Сформулируйте отрицания следующих высказываний или высказывательных форм:
- а) «Эльбрус — высочайшая горная вершина Европы«;
- б) «2>=5«;
- в) «10 Ответ]5.4. а)«Эльбрус — не высочайшая горная вершина Европы»; б)«2 =7»; г)«не все натуральные числа целые»; д)«не через любые три точки на плоскости можно провести окружность»; е)«теннисист Кафельников проиграл финальную игру»; ж)«мишень не поражена первым выстрелом»; з)«это утро не ясное или оно не теплое» (Пояснение. Пусть А = «это утро ясное», а B = «это утро теплое». Тогда «это утро ясное и теплое» можно записать как А•В, отрицанием чего является
, что соответствует высказывательной форме «это утро не ясное или оно не не теплое«; и)«число n не делится на 2 и оно делится на 3»; к)«этот треугольник не равнобедренный или он не прямоугольный»; л)«не каждый ученик писал контрольную своей ручкой» (вариант: «кто-то писал контрольную не своей ручкой»).
5.5. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:
- а) «5 10«;
- б) «10>9«, «10 Ответ]5.5. Являются отрицаниями друг друга: б), г), д), к);
не являются отрицаниями друг друга: а), в), е), ж), з), и).
5.6. Определите значения истинности высказываний:
- а) «наличия аттестата о среднем образовании достаточно для поступления в институт«;
- б) «наличие аттестата о среднем образовании необходимо для поступления в институт«;
- в) «если целое число делится на 6, то оно делится на 3«;
- г) «подобие треугольников является необходимым условием их равенства«;
- д) «подобие треугольников является необходимым и достаточным условием их равенства«;
- е) «треугольники подобны только в случае их равенства«;
- ж) «треугольники равны только в случае их подобия«;
- з) «равенство треугольников является достаточным условием их подобия«;
- и) «для того, чтобы треугольники были неравны, достаточно, чтобы они были неподобны«;
- к) «для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны«.
[ Ответ ] 5.6. Истинны: б), в), г), з), к), и);
ложны: а), д), е), ж).5.7. Подставьте в приведённые ниже высказывательные формы вместо логических переменных a, b, c, d такие высказывания, чтобы полученные таким образом составные высказывания имели смысл в повседневной жизни:
5.8. Формализуйте следующий вывод: «Если a и b истинны, то c — истинно. Но c — ложно: значит, a или b ложны».
[ Ответ ] 5.8..
5.9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: «Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги«.
Формализуйте также ответ сына: «Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди«.
[ Ответ ] 5.9. Решение. Введем обозначения для логических высказываний: а — «ты будешь говорить правду»; b — «тебя возненавидят люди»; c — «тебя возненавидят боги». Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так:. А ответ сына — так:
.
5.10. Пусть a = «это утро ясное«, а b = «это утро теплое«. Выразите следующие формулы на обычном языке:
📽️ Видео
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать
8 класс, 8 урок, Ромб и квадратСкачать
Прямоугольник. 8 класс.Скачать
Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать
№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать
Чему равна площадь четырёхугольника ABCD, если его диагонали разбивают четырёхугольникСкачать
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать
Квадрат. 8 класс.Скачать
Диагонали прямоугольника равны.Скачать
Периметр прямоугольника. Как найти периметр прямоугольника?Скачать
№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать
В четырехугольник вписан ромб, стороны которого параллельны диагоналям четырехугольника.Скачать
ОГЭ/База Все прототипы задач на четырехугольникиСкачать
Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать
Площадь прямоугольника. Как найти площадь прямоугольника?Скачать
Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать











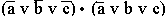
 .
.

















 д)
д)