Дан параллелограмм вершины которого лежат на одной окружности

Рассмотрим применение простейшего движения плоскости, такого как вращение (поворот) при решении задач элементарной геометрии на вычисление и доказательство.

При решении задач используются основные свойства движения. Так, всякое движение переводит:

прямую в прямую, а параллельные прямые — в параллельные прямые,

отрезок — в отрезок, а середину отрезка — в середину отрезка,

угол — в равный ему угол,

точки, не лежащие на одной прямой — в точки, не лежащие на одной прямой,

полуплоскость — в полуплоскость.

Даны две окружности 1(O1,r) и 2(O2,r), каждая из которых проходит через центр другой. Через точку А пересечения окружностей проведена прямая, пересекающая окружности в точках M и H. Найти угол между касательными, проведенными к окружностям в точках M и H.

Пусть 1 — касательная к окружности 1 в точке H, а 2 — касательная к окружности 2 в точке М. В треугольнике O1BO2 имеем O1O2=O1B=O2B. Аналогично O1O2=O1A=O2A в треугольнике O!AO2. Тогда BO1A=BO2A=120. Отсюда следует, что BO2A=BO1A=120. В треугольнике MBH получим BMA=BHA=60. Тогда MBH=60. Рассмотрим поворот вокруг точки В на угол 600. RB60:O1O2, MH. Значит RB60:O1MO2H. Тогда RB60:12, так как по свойству касательной 1 O1M, 2 O2H. Следовательно, угол между прямыми 1 и 2 равен 60.

На катетах CA и CB равнобедренного прямоугольного треугольника ABC выбраны точки D и E так, что CD = CE. Прямые, проведенные через точки D и C перпендикулярно к AE, пресекают гипотенузу AB соответственно в точках К и H. Доказать, что KH = HB.

Рассмотрим поворот вокруг точки C на 90. RC90:A B, DE, EE1, CC. Значит RC90:AEBE1, CECE1. Следовательно, AEBE1, CE = CE1. Так как CD=CE, то CD=CE1. По условию DKAE и CHAE. Тогда BE1||CH||DK. По теореме Фалеса имеем BH=HK.

В прямоугольном треугольнике АВС проведена медиана СМ. На катетах АС и ВС вне треугольника построены квадраты АСКН и ВСДЕ. Доказать, что прямые СМ и ДК перпендикулярны.

Рассмотрим поворот вокруг точки С на 900:

Следовательно, . Тогда В треугольнике АВК1 отрезок СМ является средней линией, поэтому СМ//ВК1. Тогда , так как .

Доказать, что биссектрисы внутренних углов параллелограмма при пересечении образуют прямоугольник.

Пусть дан параллелограмм АВСД, АА1, ВВ1, СС1 и ДД1 — биссектрисы его внутренних углов; К, Н, М, Р — точки их пересечения. Надо доказать, что четырехугольник КНМР является прямоугольником. Рассмотрим поворот вокруг точки пересечения диагоналей параллелограмма на 1800, то есть центральную симметрию относительно точки .

Тогда . Следовательно, четырехугольник КНМР — параллелограмм, так как его диагонали в точке пересечения делятся пополам. В параллелограмме АВСД имеем: . Значит . Тогда в треугольнике АВК найдем . В параллелограмме КНМР получили , следовательно этот параллелограмм — прямоугольник.

Дан равносторонний треугольник АВС и произвольная точка М. Доказать, что длина большего из трех отрезков МА, МВ, МС не больше суммы длин двух других.

Пусть ВМ — наибольший из указанных отрезков. Рассмотрим поворот вокруг точки В на 600.

Поэтому АМ=СМ1, ВМ=ВМ1. Следовательно, треугольник МВМ1 будет равносторонним. Поэтому МВ=ММ1. Но в треугольнике МСМ1: ММ1 2 = LQ . MN = x . 3x = 3x 2 ,NL = .

Таким образом, стороны треугольника QLM равны QL = x, QM = 2x и LM = NL =. Следовательно, этот треугольник — прямоугольный. Его углы равны

QLM = 90 o ,QML = 30 o ,LQM = 60 o .

а углы треугольника LMN равны 120 o , 30 o , 30 o .

Два квадрата BCDA и BKMN имеют общую вершину В. Докажите, что медиана ВЕ треугольника АВК и высота ВF треугольника СBN лежат на одной прямой. (Вершины квадратов перечислены против часовой стрелки).

Для доказательства того, что медиана ВЕ и высота BF лежат на одной прямой, достаточно показать, что прямая ВЕ перпендикулярна прямой CN.

Применим поворот плоскости вокруг точки В на угол 90° против часовой стрелки. При этом повороте вершина К перейдет в вершину N, вершина С — в вершину А. Обозначим через A` образ точки А при данном повороте. Отметим, что точки С, В и A` лежат на одной прямой, причем точка В делит пополам отрезок СA`. Поскольку поворот плоскости вокруг данной точки на заданный направленный угол сохраняет простое отношение трех точек, то середина Е отрезка АК перейдет в середину E` отрезка A`N. В силу того, что мы применяем поворот вокруг точки В на угол +90°, то ЕВE` = 90°. Далее рассмотрим треугольник СA`N. В этом треугольнике BE` — средняя линия. Значит, прямая ВЕ` параллельна прямой CN. Следовательно, прямая ВЕ перпендикулярна прямой CN, т.е. точки Е, В, F лежат на одной прямой.

Примечание. В ходе решения данной задачи было установлено, что отрезок ВЕ не только перпендикулярен отрезку CN, но и равен его половине. Таким образом, требование предложенной задачи можно переформулировать следующим образом: доказать, что медиана ВЕ треугольника АВК перпендикулярна отрезку СN и равна его половине.

На сторонах ВС и CD квадрата ABCD взяты точки М и К так, что периметр треугольника СМК равен удвоенной стороне квадрата. Найдите величину угла МАК.

Применим поворот плоскости вокруг вершины А на 90°, при котором вершина В перейдет в вершину D. Обозначим через M` образ точки М при этом повороте. Поскольку периметр треугольника СМК равен удвоенной стороне квадрата, то СМ + МК + СК = ВС + CD. Так как ВС = ВМ + МС, CD = СК + KD, то СМ + МК + СК = ВМ + МС + СК + КD. Откуда следует, что МК = ВМ + КD.

При повороте плоскости вокруг точки А на 90° отрезок ВМ переходит в отрезок DM`, отрезок АМ — в отрезок AM`, следовательно, МК = DM` + KD, АМ` = АМ. Но точка D лежит между точками M` и К, значит, DM` + KD = M`K. Таким образом, мы установили, что треугольники АМК и АМ`К равны. Следовательно, ЃЪМАК = ЃЪМ`АК = 45°.

Внутри равнобедренного прямоугольного треугольника АВС (ЃЪАСВ=90°) взята точка М такая, что AM = , BM = , CM = 4 . Найти площадь треугольника АВС.

Для того чтобы найти площадь равнобедренного прямоугольного треугольника достаточно знать длину его катета или гипотенузы. Для нахождения длины катета треугольника рассмотрим треугольник МВС. В этом треугольнике нам известны длины двух сторон BM = , CM = 4 . Для определения длины третьей стороны нам необходимо знать угол между ними. Для этого применим поворот плоскости вокруг вершины С на угол 90°. При этом повороте вершина А перейдет в вершину В, а точка М — в некоторую точку М`.

Рассмотрим треугольник МСМ`. Поскольку СМ=СМ`=4, ЃЪMСM`=90°, то по теореме Пифагора получаем, что MM`= 4. Так как при повороте плоскости вокруг точки С на 90° точка А переходит в точку В, то отрезок АМ перейдет в отрезок ВМ`. Теперь рассмотрим треугольник МВМ`. В этом треугольнике мы знаем длины всех трех сторон: BM`= , BM = , MM`= 4 . Следовательно, по теореме косинусов находим, что

Откуда получаем, что . Значит, ЃЪВMМ`=60°.

По свойству равнобедренного треугольника имеем, что ЃЪСMM`=45°. Итак, ЃЪBMС=105° . По теореме косинусов из треугольника ВМС получаем, что

На сторонах АВ и АС правильного треугольника АВС выбраны точки D и E так, что AD + AE = AB. Доказать, что DC = BE, и найти величину угла DOE, где О — центр тяжести треугольника АВС.

Анализируя условие задачи, приходим к заключению, что каждая сторона треугольника АВС видна из центра О под одним и тем же углом 120°, что позволяет положить в основу решения задачи поворот вокруг точки О на данный угол. При этом повороте правильный треугольник АВС переходит в себя, т.е. данный поворот входит в группу симметрий рассматриваемой фигуры.

Заметим, что при рассматриваемом повороте точка С переходит в точку В, а точка D переходит в точку Е.

Значит, отрезок СD переходит в отрезок ВЕ. Следовательно, они равны. Поскольку при этом повороте точка D переходит в точку Е, значит, угол DOE = 120°.

На сторонах правильного треугольника, вне его, построены квадраты. Доказать, что их центры являются вершинами правильного треугольника.

При повороте вокруг точки О на 120° по часовой стрелке квадрат ABRL переходит в квадрат ВСNM, а квадрат ВСNM переходит в квадрат САED, квадрат САED переходит, в свою очередь, в квадрат АВRL. Важно заметить, что при этом повороте точка O1 переходит в точку О2, а точка О2 переходит в точку О3. Значит, стороны О1О2, О2О3, О1О3 равны между собой. Следовательно, треугольник О1О2О3 — правильный.

При повороте вокруг точки О на 120° квадрат ABRL переходит в квадрат ВСNM, а квадрат ВСNM переходит в квадрат САED, квадрат САED переходит, в свою очередь, в квадрат АВRL. Важно заметить, что при этом повороте точка O1 переходит в точку О2, а точка О2 переходит в точку О3. Значит, стороны О1О2, О2О3, О1О3 равны между собой. Следовательно, треугольник О1О2О3 — правильный.

Точка В лежит между точками А и С. На отрезках АВ и ВС в одной полуплоскости с границей АС построены правильные треугольники АВЕ и ВСF. Точки М и N — середины отрезков АF и СЕ. Доказать, что треугольник ВMN правильный.

При повороте вокруг точки В на направленный угол 60° точка С перейдет в точку F, а точка Е перейдет в точку А. Следовательно, отрезок СЕ перейдет в отрезок AF. Поскольку поворот, как и всякое движение плоскости, сохраняет простое отношение трех точек, значит, середина N отрезка СЕ перейдет в середину отрезка AF, т.е. точка N перейдет в точку М при повороте плоскости вокруг точки В на угол 60°. Таким образом, мы доказали, что треугольник BMN — правильный.

В прямоугольном треугольнике СМ — медиана. Па катетах АС и ВС, вне треугольника ABC, построены квадраты ACFN и BCDE. Доказать, что:

• 1) прямые СМ и DF перпендикулярны;
• 2)CM = 0,5DF.

За центр поворота примем вершину прямого угла. Такой выбор центра поворота плоскости определяет и угол поворота — 90°. При повороте вокруг точки С на угол -90° вершина В прямоугольного треугольника ABC перейдет в точку В’ принадлежащую катету АС, вершина А перейдет в вершину F квадрата. При этом гипотенуза АВ отобразится на отрезок FB’ а его середина М перейдет в середину М’ отрезка FB’.

Заметим, что отрезки СМ и СМ’ взаимно перпендикулярны и равны. Это позволяет сделать следующее заключение: для того, чтобы доказать, что медиана СМ треугольника ABC перпендикулярна отрезку FD и равна его половине, достаточно показать, что отрезок СМ’ является средней линией треугольника FB’D, что доказывается очень просто. Точка С есть середина отрезка DB’ а точка М’ есть середина отрезка FB’. Значит, СМ’ — средняя линия треугольника FB’D.

В правильном шестиугольнике ABCDEF точки М и N — середины сторон CD и DE, Р — точка пересечения отрезков AM и BN.

Найдите угол между прямыми AM и BN.

Докажите, что треугольник АВР и четырехугольник MDNP — равновелики.

Применим поворот плоскости вокруг центра правильного шестиугольника на 60°, переводящем вершину А в вершину В. При этом повороте сторона CD перейдет в сторону DE, значит, точка М, как середина отрезка CD, перейдет в точку N — середину отрезка DE. Следовательно, прямая AM при повороте плоскости вокруг точки О на 60° переходит в прямую BN. По свойству поворота угол между ними равен углу поворота, т.е. 60°. Далее отметим, что при этом повороте плоскости пятиугольник AMDEF переходит в пятиугольник BNEFA. Замечательным свойством этих пятиугольников является то, что они содержат общую часть — это пятиугольник APNEF.

Если из пятиугольников AMDEF и BNEFA вырезать их общую часть -пятиугольник APNEF, то получим равновеликие фигуры — треугольник АВР и четырехугольник MDNP.

Вокруг квадрата ABCD описан параллелограмм A₁B₁C₁D₁. Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, образуют квадрат.

Параллелограмм A₁B₁C₁D₁ описан около квадрата ABCD так, что точка А лежит на стороне A₁B₁, точка В — на стороне B₁C₁ , точка С — на стороне C₁D₁, а точка D — на стороне A₁D₁. Из вершин параллелограмма A₁B₁C₁D₁ опустим перпендикуляры т₁, т₂, т₃, т₄ на стороны квадрата ABCD. Для того, чтобы доказать, что эти перпендикуляры образуют квадрат, достаточно показать, что при повороте плоскости вокруг центра О квадрата ABCD на 90° прямые т₁, т₂, т₃, т₄ переходят друг в друга. Прежде всего отметим, что при этом повороте точки A₁, B₁, C₁, D₁ переходят в точки А₂, В₂, С₂, D₂. А это значит, что образом стороны A₁B₁ параллелограмма A₁B₁C₁D₁ при повороте плоскости вокруг точки О на 90°служит сторона А₂В₂. Следовательно, отрезок А₂В перпендикулярен отрезку АВ₁. Далее прямая A₁D₁ при повороте плоскости вокруг точки О на 90° перейдет в прямую A₂D₂. Поскольку прямые B₁C₁ и A₁D₁ параллельны, то отрезок АА₂ перпендикулярен отрезку ВВ₁ Таким образом, мы установили, что точка А2 является ортоцентром треугольника АВВ₁. Значит, прямая т₁ при повороте плоскости вокруг точки О на 90° переходит в прямую т₂. Аналогичными рассуждениями можно установить, что при этом повороте плоскости прямая т₂ переходит в прямую т₃, а прямая т₃ — в прямую т₄, прямая т₄ — в прямую т₁ . Следовательно, при пересечении они образуют квадрат.

Доказать, что две трапеции равны, если равны их соответственные стороны.

Доказательство. На плоскости зададим две трапеции A₁B₁C₁D₁ и A₂B₂C₂D₂ с основаниями A₁B₁ и C₁D₁, A₂B₂ и C₂D₂. Пусть A₁B₁ = A₂B₂ , B₁C₁ = B₂C₂, C₁D₁ = C₂D₂, A₁ D₁ = A₂ D₂. Можно показать, что при заданных условиях расстояния между основаниями этих трапеций, углы D₁A₁B₁ и D₂A₂B₂ равны. Для того чтобы доказать, что A₁B₁C₁D₁ = А₂В₂С₂D₂ покажем, что существует движение плоскости, которое переводит одну из этих трапеций в другую. Рассмотрим параллельный перенос, определяемый вектором . При этом переносе трапеция A₁B₁C₁D₁ перейдет в равную ей трапецию . Возможны два случая расположения трапеции относительно трапеции A₂B₂C₂D₂. Первый, когда они лежат в одной полуплоскости, определяемой прямой А₂В₂; второй, когда они не лежат в одной полуплоскости с границей А₂В₂. Обозначим через а угол между прямыми A₁B₁ и А₂В₂. Заметим, что угол между прямыми, содержащими меньшие основания трапеции тоже равен а. В первом случае рассмотрим поворот плоскости вокруг точки А₂ на угол по часовой стрелки. При этом отрезок перейдет в отрезок А₂В₂; прямая в прямую C₂D₂ . Поскольку , то при повороте вокруг точки А₂ на угол образом точки будет служить точка D₂. Аналогичным образом получаем, что образ точки совпадает с точкой С₂.

Итак, мы показали, что при композиции параллельного переноса на вектор и поворота плоскости вокруг точки А₂ на угол трапеция A₁B₁C₁D₁ переходит в трапецию A₂B₂C₂D₂. Значит они равны. Пусть теперь трапеции и A₂B₂C₂D₂ не лежат в одной полуплоскости с границей А₂В₂. Рассмотрим поворот плоскости вокруг точки А₂ на угол 360° по часовой стрелке. Аналогичными рассуждениями можно показать, что при этом повороте трапеция перейдет в трапецию A₂B₂C₂D₂. Если рассмотреть поворот плоскости вокруг точки А₂ на угол по часовой стрелке, то трапеция перейдет в некоторую трапецию .

Два одинаково ориентированных квадрата ABCD и AB₁C₁D₁ на плоскости имеют общую вершину A. Доказать, что центры O₁, О₂ этих квадратов и середины О₃ и О₄ отрезков A₁D и ВС₁ образуют квадрат.

Решение. Как известно четырехугольник является квадратом тогда и только тогда, когда при повороте плоскости вокруг середины одной из его диагоналей он переходит в себя. Для решения данной задачи воспользуемся аналитическим способом задания поворота. На плоскости зададим ПДСК с началом в точке А и единичными векторами и . Обозначим через угол между вектором и вектором . Тогда относительно заданной ПДСК А вершины квадратов ABCD и AB₁C₁D₁ имеют следующие координаты:

Зная координаты точек В и D, D иВ₁,А и С₁,В и D₁, найдем координаты середин этих отрезков. Имеем:

Теперь найдем координаты середины О диагонали О₂О₄. Имеем:

Составим формулы поворота плоскости вокруг точки О на угол -90°. Получим, что

Поскольку , то формулы поворота плоскости вокруг точки о на угол -90 принимают следующий вид:

Найдем образ точки O₁ при повороте . Имеем:

Заметим, что образ точки О₁ при повороте совпадает с вершиной О₂. Теперь найдем образ этой вершины. Имеем:

Заметим, что образ точки О₂ при повороте совпадает с вершиной О₃. Теперь найдем образ этой вершины. Имеем:

Заметим, что образ точки О₃ при повороте совпадает с вершиной О₄. Аналогичным образом можно показать, что образ вершины О₄ при повороте совпадает с вершиной O₁. Следовательно, четырехугольник О₁О₂О₃О₄ есть квадрат.

Рассмотрим вращение плоскости вокруг точки для решения задач на построение.

Пусть а₁ и а₂ — две различные прямые, пересекающиеся в точке О. Пусть Х — произвольная точка плоскости. Построим точку Х, симметричную точке Х относительно прямой а₁, а затем построим точку Х, симметричную точке Х относительно прямой а₂ (Рис. 3.19) Преобразование, которое сопоставляет точке Х точку Х указанным образом, называется поворотом относительно точки О.

Если прямые а₁ и а₂ перпендикулярны, то поворот сводится к симметрии относительно точки О. Если прямые а₁ и а₂ не перпендикулярны, то угол ХОХ не зависит от точки Х и равен удвоенному острому углу, под которым пересекаются прямые а₁ и а₂. Этот угол называется углом поворота. Наметим доказательство этого утверждения.

Пусть точка Х находится внутри острого угла, образованного прямыми а₁, а₂, и ₁, ₂ — части этого угла, на которые он разбивается полупрямой ОХ (рис. 3.19). Тогда по свойству симметрии относительно прямой угол ХОХ равен 2₁, а угол ХОХ равен 2₂. Соответственно угол ХОХ равен 2₁2₂2(₁₂). Читателю предлагается рассмотреть случай, когда точка Х лежит внутри тупого угла, образуемого прямыми а₁ и а₂, а также случай, когда прямые а₁ и а₂ перпендикулярны.

Поворот прямой а на угол вокруг центра О выполняется так.

Строится ОМа (Ма). Затем в нужном направлении производится поворот отрезка ОМ на угол в положение ОМ, после чего строится прямая аОМ.

Отметим следующее очевидное свойство отражения фигур, обладающих осевой симметрией.

Преобразование симметрии относительно оси s, выполненное по отношению к фигуре, обладающей хотя бы одной осью симметрии, может быть заменено поворотом (в частном случае параллельным переносом).

Подвергнем фигуру F₁ (Рис. 3.20) преобразованию симметрии относительно прямой s. В результате получим фигуру F₂, противоположно ориентированную. Выполним для фигуры F₂ преобразование симметрии относительно оси s₂ (s₂ есть, очевидно, образ оси s₁). Тогда фигура F₂ преобразуется в себя и будет одинаково ориентирована с F₁, следовательно, фигуры F₁ и F₂ могут быть совмещены поворотом вокруг точки О пересечения оси симметрии фигуры и оси s. Если эти оси параллельны, то достаточно выполнить некоторый параллельный перенос.

Поворот на некоторый угол 180 имеет применение при решении задач на построение. При этом поворот выполняется либо по отношению ко всей фигуре чертежа-наброска, либо по отношению к отдельным элементам фигуры.

Даны точка О и прямые а и b, не проходящие через нее. Из точки О как из центра провести такую окружность, чтобы дуга ее, заключенная между данными прямыми, была видна из точки О под данным острым углом .

Анализ. Допустим, что задача решена, — искомая окружность, А и В — концы дуги, заключенной между данными прямыми, АОВ = (Рис. 3.21.). Если осуществить поворот прямой а около точки О на угол , то точка А попадет в точку В. Следовательно, точка В может быть найдена как пересечение образа прямой а с прямой b. После этого легко строится искомая окружность.

Внутри данного треугольника АВС найти точку Р, сумма расстояний которой до вершин А, В и С была бы наименьшей.

Анализ. Пусть Р₁ — искомая точка. Для выяснения ее геометрических свойств повернем сначала треугольник АВР₁ на 60 вокруг точки А (Рис. 3.22). Тогда АР₁+Р₁В+Р₁С=ВР+Р₁Р+Р₁С.

Эта сумма будет наименьшей, если ВС — прямая. Аналогичные рассуждения относительно треугольника ВР₁С (тогда В переходит в В) показывают, что АВ — прямая.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Олимпиадные задания по математике 8 — 11 класс

Видео:№9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости αСкачать

Олимпиадные задания по математике 8 — 11 класс

Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Олимпиадные задания по математике 8 класс

1. На доске была нарисована система координат и отмечены точки A(1;2) и B(3;1). Систему координат стерли. Восстановите ее по двум отмеченным точкам.

2. В некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Верно ли, что треугольник равнобедренный?

3. В правильном шестиугольнике АВСDEF на прямой AF взята точка X так, что угол XСD = 45 o . Найдите угол FXE.

4. Около четырехугольника ABCD можно описать окружность. Точка p – основание перпендикуляра, опущенного из точки А на прямую ВС, Q – из А на DC, R – из D на АВ и Т – из D на ВС. Докажите, что точки p, Q, R и T лежат на одной окружности.

5. Восстановите остроугольный треугольник по ортоцентру и серединам двух сторон.

6. Противоположные стороны выпуклого шестиугольника ABCDEF параллельны. Назовем его «высотами» векторы с концами на прямых, содержащих противолежащие стороны, перпендикулярные им и направленные от AB к DE, от EF к BC и от CD к AF. Докажите, что вокруг этого шестиугольника можно описать окружность тогда и только тогда, когда сумма его «высот» равна нулевому вектору.

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Олимпиадные задания по математике 8 класс

1. Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.

2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК .

3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.

4. В трапеции ABCD : AB = BC = CD , CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС , проходит через середину BD .

5. Пусть AA ₁ и BB ₁ – высоты неравнобедренного остроугольного треугольника АВС , М – середина АВ . Окружности, описанные около треугольников AMA ₁ и BMB ₁ пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К , М и L лежат на одной прямой.

6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Олимпиадные задания по математике 9 класс

1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне ( исследование вопроса о количестве решений не требуется ).

2. В выпуклом четырехугольнике ABCD Ð ABC = 90 0 , Ð BAC = Ð CAD , AC = AD , DH — высота треугольника ACD . В каком отношении прямая BH делит отрезок CD ?

3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС . На окружностях (в одной полуплоскости относительно АС ) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC . Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB . Докажите, что точки M , K , F и L лежат на одной окружности.

4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A’ , B’ , C’ — точки ее касания со сторонами BC , CA , AB соответственно. Докажите, что, если CA’ = AB , то прямые OM и AB перпендикулярны.

5. Дан треугольник АВС . Точка О 1 — центр прямоугольника ВСDE , построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О 2 и О 3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО 1 , ВО 2 и СО 3 пересекаются в одной точке.

6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости?

Видео:8 класс, 4 урок, ПараллелограммСкачать

Олимпиадные задания по математике 9 класс

9.1. В выпуклом четырехугольнике АВС D Е – середина CD , F – середина А D , K – точка пересечения АС и ВЕ . Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС .

9.2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С .

9.3. Дан квадрат ABCD . Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD .

9.4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p . Точки X и Y – ортогональные проекции точки p на прямые AC и BC . Докажите, что прямая XY перпендикулярна медиане треугольника ABC , проведенной из вершины C .

9.5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M , Ð AMB = 60 ° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL . Прямая KL пересекает описанную около ABCD окружность в точках p и Q . Докажите, что pK = LQ .

9.6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3 .

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Олимпиадные задания по математике 9 класс

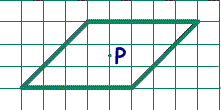
1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.

2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.

4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)

5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?

6. Фиксированы две окружности w₁ и w₂, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w₁ и w2 соответственно, а треугольник XYZ содержит окружности w₁ и w₂. Докажите, что центры окружностей, вписанных в треугольники XYZ , лежат на одной прямой.

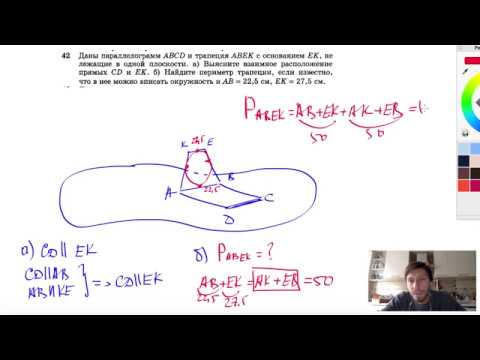
Видео:№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать

Олимпиадные задания по математике 10 класс

10.1. Е и F – середины сторон ВС и AD выпуклого четырехугольника АВС D . Докажите, что отрезок EF делит диагонали АС и BD в одном и том же отношении.

10.2. Существует ли в пространстве замкнутая самопересекающаяся ломаная, которая пересекает каждое свое звено ровно один раз, причем в его середине?

10.3. На доске была нарисована окружность с отмеченным центром, вписанный в нее четырехугольник, и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырехугольник (сохранив одну вершину) и вписанную окружность (сохранив ее центр). Восстановите какую-нибудь из стертых вершин четырехугольника, пользуясь только линейкой и проведя не более шести линий.

10.4. В треугольнике АВС : М – точка пересечения медиан, О – центр вписанной окружности. Докажите, что если прямая ОМ параллельна стороне ВС , то точка О равноудалена от сторон АВ и АС .

10.5. Трапеция АВС D с основаниями AB и CD вписана в окружность. Докажите, что четырехугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC , BC , AD и BD , является вписанным.

10.6. В тетраэдре DABC : Ð ACB = Ð ADB , ( С D ) ^ ( АВС ). В треугольнике АВС дана высота h , проведенная к стороне АВ , и расстояние d от центра описанной окружности до этой стороны. Найдите длину CD .

Видео:🔥ЕГЭ 2021/Дан параллелограмм ABCD с острым углом А. На продолжении стороны AD за точку D взята такаяСкачать

Олимпиадные задания по математике 10 класс

1. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны?

2. Даны радиусы r и R двух непересекающихся окружностей. Общие внутренние касательные этих окружностей перпендикулярны. Найдите площадь треугольника, ограниченного этими касательными, а также общей внешней касательной.

3. Дан четырехугольник ABCD. A’, B’, C’ и D’ – середины сторон BC, CD, DA и AB соответственно. Известно, что AA’ = CC’ и BB’ = DD’. Верно ли, что ABCD параллелограмм?

4. В треугольнике АВС угол А равен 120 o . Докажите, что расстояние от центра описанной окружности до ортоцентра равно АВ + АС.

6. Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причем их периметры одинаковы. Существует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)?

6. Дан треугольник ABC и точки p и Q. Известно, что треугольники, образованные проекциями p и Q на стороны ABC, подобны (соответствуют друг другу вершины, лежащие на одних и тех же сторонах исходного треугольника). Докажите, что прямая pQ проходит через центр описанной окружности треугольника ABC.

Видео:Геометрия Главная задача по теме параллелограммСкачать

Олимпиадные задания по математике 11 класс

1. AD и BE – высоты треугольника АВС . Оказалось, что точка C’ , симметричная вершине С относительно середины отрезка DE , лежит на стороне AB . Докажите, что АВ – касательная к окружности, описанной около треугольника DEC’ .

2. Прямая а пересекает плоскость α . Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α ?

3. Дана неравнобокая трапеция ABCD ( AB || CD ). Произвольная окружность, проходящая через точки А и В , пересекает боковые стороны трапеции в точках p и Q , а диагонали – в точках M и N . Докажите, что прямые pQ , MN и CD пересекаются в одной точке.

4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.

5. В выпуклом четырехугольнике ABCD : AC ⊥ BD , ∠ BCA = 10°, ∠ BDA = 20°, ∠ BAC = 40°. Найдите ∠ BDC . ( Ответ выразите в градусах. )

6. Пусть AA ₁, BB ₁ и CC ₁ – высоты неравнобедренного остроугольного треугольника АВС ; окружности, описанные около треугольников АВС и A ₁ B ₁ C , вторично пересекаются в точке Р , Z – точка пересечения касательных к описанной окружности треугольника АВС , проведённых в точках А и В . Докажите, что прямые АР , ВС и ZC ₁ пересекаются в одной точке.

Видео:Доказать, что точки лежат на одной окружностиСкачать

Олимпиадные задания по математике 11 класс

1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?

2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей.

3. В остроугольном треугольнике АВС проведены высоты АА₁ и ВВ₁. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А₁СВ₁.

4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C₁ — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM₁ и BM₂. Точки A₁ и B₁ определяются аналогично. Докажите, что прямые АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.

6. К двум окружностям w₁ и w₂, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w₁ и w₂ в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке p. Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы).

Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами:

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Метод вращения

Указание. Пусть KLMP — искомый квадрат. Тогда центр О квадрата совпадает с центром параллелограмма. Повернем всю фигуру вокруг точки О на 90°; при этом точка М перейдет в точку Р, прямая I (11AD, Mel) перейдет в V, точка Я (ОЯ 1 I, Я е I) перейдет в Я’. Отсюда, выполняя обратный поворот на 90°, можно получить точку М (так как ОН _L Z), а следовательно, получим диагонали КМ и PL.

6.3. Даны две окружности О_а(г_а) и 0₂(г₂), точка М и угол а. Построить равнобедренный треугольник АВС (АВ = АС) так, чтобы угол А равнялся а, вершина А совпадала с точкой М, а две другие вершины лежали бы на окружностях 0₁(г₁) и 0₂(г₂).

Указание. Повернуть вокруг точки М одну из данных окружностей на угол а и найти точки пересечения с другой окружностью. Задача может иметь одно, два или ни одного решения.

• 6.4. Даны точка А, прямая а и окружность О (г). Построить равносторонний треугольник с вершиной в точке А так, чтобы другие его вершины лежали соответственно на прямой а и окружности О (г).
• 6.5. В данный квадрат ABCD вписать равносторонний треугольник, одна из вершин которого дана на стороне квадрата.
• 6.6. Даны две прямые: р и q и точка А. Построить равносторонний треугольник так, чтобы одна его вершина совпадала с точкой А, а две другие лежали на прямых р ид.
• 6.7. На двух данных отрезках найти такую пару точек, что поворот вокруг данной точки на 45° отображает одну точку пары на другую.
• 6.8. Указать соответственно на данных прямой и отрезке такие две точки, чтобы одну из них можно было бы отобразить на другую поворотом вокруг данной точки на 30°.
• 6.9. На данных окружности и прямой найти такие пары точек, что одна точка является образом другой при повороте вокруг данной точки на 72°.
• 6.10. Даны полоса с краями а и Ъ и точка Р, принадлежащая этой полосе (Р g а, Р € Ь). Найти на ее краях а и b соответственно такие точки А и В, что РА = РВ и ZAPB = 90°.
• 6.11. Даны окружности (С^; 3 см), (0₂; 4 см) и точкам. Найти на данных окружностях соответственно точки А и В такие, чтобы AM = МВ и ZAMB = 60°.
• 6.12. На прямыху = Зх + 1 и у = -2х + 3 найти соответственно точки А и В, чтобы они находились на одинаковом расстоянии от начала координат и ZAOB = 90°.
• 6.13. Даны окружность и треугольник. Построить такой отрезок, чтобы концы его принадлежали данным окружности и сторонам треугольника, находились на одинаковом расстоянии от данной точки и были видны из нее под углом 120°.
• 6.14. Даны произвольный треугольник АВС и точка Р, принадлежащая внутренней области треугольника. Указать на сторонах ВС и АС соответственно точки К и М такие, что РК = КМ и ZKPM = 45°.
• 6.15. Построить равносторонний треугольник так, чтобы одной его вершиной была данная точка Р, другая принадлежала данной прямой а, третья — прямой Ъ.
• 6.16. Даны угол и точка А внутри него. Построить равнобедренный прямоугольный треугольник, вершиной прямого угла которого является точка А, а две другие вершины принадлежат сторонам данного угла.
• 6.17. Даны окружность, квадрат и точка Р. Построить равнобедренный треугольник РАВ (РА = РВ), вершины А и В которого принадлежат окружности и стороне квадрата, a ZAPB = 45°.
• 6.18. Построить равносторонний треугольник так, чтобы его вершины принадлежали трем данным параллельным прямым.
• 6.19. Даны полоса с краями а и с и прямая Ь, принадлежащая полосе. Построить ромб ABCD так, чтобы его вершины А, В и С принадлежали соответственно прямым а,Ь и с, a ZABC = 60°.
• 6.20. Построить квадрат так, чтобы три его вершины принадлежали трем данным прямым.
• 6.21. Построить равнобедренный прямоугольный треугольник так, чтобы вершины его острых углов принадлежали данным окружностям, а вершиной прямого угла являлась данная точка.
• 6.22. В данный квадрат вписать равносторонний треугольник так, чтобы одна из его вершин совпала с вершиной квадрата, а две другие принадлежали сторонам квадрата.
• 6.23. На сторонах АВ и АС треугольника АВС построены квадраты ABNM и ACQP, расположенные с треугольником АВС в различных полуплоскостях соответственно с границами АВ и АС. Доказать, что: а) МС = ВР; б) МС1 ВР.
• 6.24. Дан квадрат ABCD. Через центр этого квадрата проведены две взаимно перпендикулярные прямые, отличные от прямых АС и BD. Доказать, что фигуры, являющиеся пересечением этих прямых с квадратом, равны.
• 6.25. Отрезки, концами которых служат внутренние точки противоположных сторон квадрата, перпендикулярны. Доказать, что эти отрезки равны.
• 6.26. Земельный участок квадратной формы был огорожен. От изгороди сохранились четыре столба на сторонах квадрата. Восстановить границу участка.
• 6.27. Через центр равностороннего треугольника проведены две прямые, угол между которыми равен 60° и которые не содержат вершин треугольника. Доказать, что отрезки этих прямых, заключенные между сторонами треугольника, равны.
• 6.28. На сторонах АВ и ВС треугольника АВС построены квадраты ABMN и BCPQ, причем квадрат ABMN и треугольник АВС принадлежат различным полуплоскостям с границей АВ, а квадрат BCPQ и треугольник АВС — одной полуплоскости с границей ВС. Доказать, что MQ1AC и MQ = AC.
• 6.29. На сторонах АВ, ВС, CD и DA квадрата ABCD от вершин А, В, С и D отложены конгруэнтные отрезки АА,, ВВ,, СС_Х и DD,. Доказать, что четырехугольник A₁B₁C₁D₁ — квадрат.
• 6.30. Хорды одной и той же окружности находятся на одинаковом расстоянии от центра окружности. Доказать, что они равны.
• 6.31. Даны две перпендикулярные прямые и точка, не принадлежащая им. Построить равносторонний треугольник с вершиной в данной точке и с двумя другими вершинами на данных прямых.
• 6.32. Построить равносторонний треугольник так, чтобы одной его вершиной была данная точка Р, другая принадлежала данной прямой а, третья — прямой Ь.
• 6.33. Построить равносторонний треугольник, имеющий одной своей вершиной данную точку А, а две другие вершины — на данных параллельных прямых.
• 6.34. Даны две параллельные прямые а, b и точка А, не принадлежащая им. Построить равнобедренный треугольник с данным углом а, вершина которого находится в данной точке А, а вершины основания лежат на прямых а и Ь.
• 6.35. Даны три параллельные прямые а, Ь, с. Построить равносторонний треугольник АВС, вершины которого лежат на данных прямых.
• 6.36. Построить равносторонний треугольник, вершины которого лежат на трех параллельных прямых, а центр — на четвертой прямой, не параллельной трем заданным.
• 6.37. В данный квадрат вписать равносторонний треугольник.
• 6.38. Построить квадрат так, чтобы три его вершины лежали на трех данных параллельных прямых.
• 6.39. Построить квадрат так, чтобы три его вершины принадлежали трем данным пересекающимся прямым.
• 6.40. Из данной точки Р, как из центра, описать дугу окружности так, чтобы концы ее лежали на двух данных окружностях, а градусная мера ее была равна градусной мере данного угла.
• 6.41. Даны две прямые, точка О и угол а. Провести такую окружность с центром О, чтобы одна из дуг этой окружности, концы которой принадлежат данным прямым, по угловой мере была равна а.
• 6.42. Даны две окружности и точка М. Построить равносторонний треугольник MNP, вершины которого N и Р принадлежат данным окружностям.
• 6.43. Даны три концентрические окружности. Построить равносторонний треугольник, вершины которого принадлежат этим окружностям.
• 6.44. Даны окружность, квадрат и точка Р. Построить равнобедренный треугольник РАВ (РА = РВ), вершины А и В которого принадлежат окружности и стороне квадрата, a ZAPB = 45°.
• 6.45. Даны угол и внутри него точка Л. Построить равнобедренный прямоугольный треугольник, вершина прямого угла которого совпадает с точкой А, а две другие вершины принадлежат сторонам угла.
• 6.46. Построить равнобедренный прямоугольный треугольник так, чтобы вершины его острых углов принадлежали данным окружностям, а вершиной прямого угла являлась данная точка.
• 6.47. Построить квадрат ABCD по его центру О и двум точкам М и N, принадлежащим прямым ВС и CD.
• 6.48. Построить квадрат ABCD по вершине А и двум точкам М и N, принадлежащим прямым ВС и CD.
• 6.49. На окружности с центром в точке О найти две такие точки С и D, что ZCOD = а, АС || BD, где А и В — две данные точки; а — величина данного угла.
• 6.50. Построить треугольник АВС, зная три точки, являющиеся центрами квадратов, построенных на сторонах треугольника, вне его.
• 6.51. Даны четыре точки К, L, М и N. Построить квадрат, стороны которого или их продолжения проходят через эти четыре точки.
• 6.52. Даны четыре точки К, L, М и N, расположенные на одной прямой. Построить квадрат, у которого продолжения двух противоположных сторон пересекают эту прямую в точках К и L, а продолжения двух других сторон — в точках М и N.

🔍 Видео

№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать

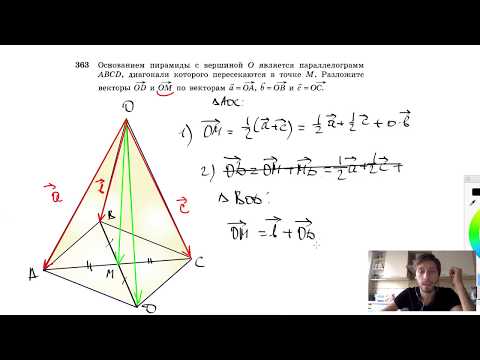
№363. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которогоСкачать

Параллелограмм. Свойства. Периметр.Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противопСкачать

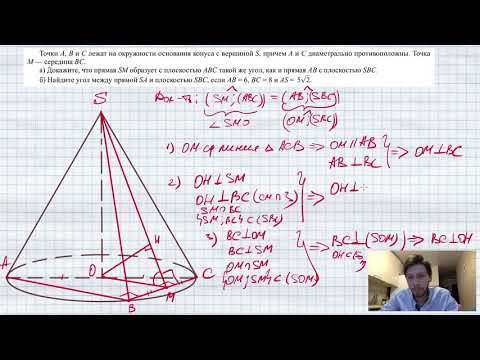
Свойства параллелограмма. 8 класс.Скачать

Вся геометрия 8 класса с нуля для ОГЭ по математике 2024Скачать