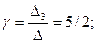Длина вектора координатами в ортогональном базисе (5 видео)

Система координат. Ортонормированный базис. Длина вектора в ортонормированном базисе.

Дата добавления: 2015-09-15 ; просмотров: 7034 ; Нарушение авторских прав

Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой- либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Декартова система координат.

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.

1-я ось – ось абсцисс

Видео:Длина вектора через координаты. 9 класс.Скачать

2-я ось – ось ординат

3-я ось – ось апликат

Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то = (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

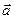
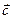
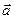
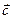
Пример. Даны векторы (1; 2; 3), (-1; 0; 3), (2; 1; -1) и (3; 2; 2) в некотором базисе. Показать, что векторы , и образуют базис и найти координаты вектора в этом базисе.

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

линейно независимы.

Тогда .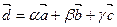

Это условие выполняется, если определитель матрицы системы отличен от нуля.

Для решения этой системы воспользуемся методом Крамера.

D₁ =

;

D₂ =

D₃ =

Итого, координаты вектора в базисе , , : .

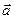
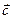
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .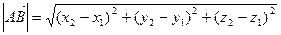

Деление вектора в заданном отношении. Операции над векторами, заданными своими координатами.

Если точка М(х, у, z) делит отрезок АВ в соотношении l/m, то координаты этой точки определяются как:

В частном случае координаты середины отрезка находятся как:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Линейные операции над векторами в координатах.

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

A =

4	3	5
6	7	1
9	1	8

B =

-1	3	-2
-4	1	2
3	-4	5

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55	-19	-32
-39	-13	26
-57	23	10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55	-19	-32
-39	-13	26
-57	23	10

-1	3	-2
-4	1	2
3	-4	5

75 /₁₈₂	-1 46 /₉₁	1 9 /₁₃
-13 /₁₄	1 2 /₇	-1
5 /₁₈₂	1 3 /₉₁	-1 2 /₁₃

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Видео:Координаты вектора. 9 класс.Скачать

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.