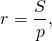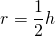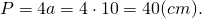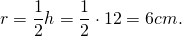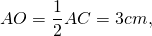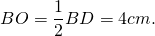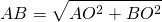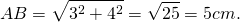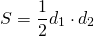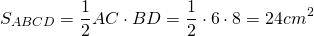Параллелограмм и окружность фигуры

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

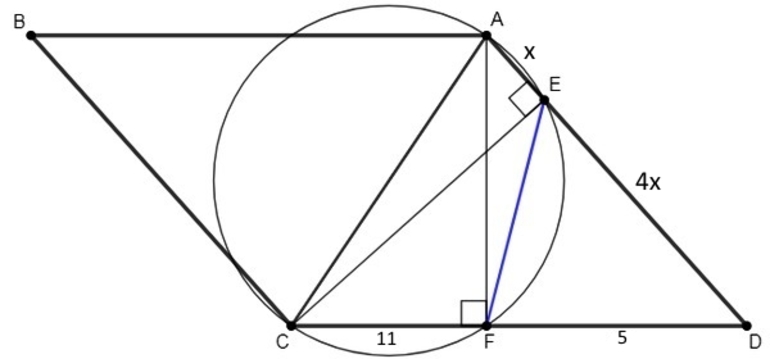
1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен

Видео:ЕГЭ Задание 16 Параллелограмм и окружностьСкачать

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
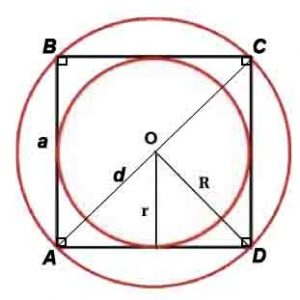
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника.

Видео:№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
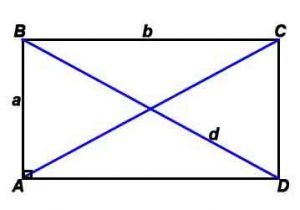
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Видео:Задание 24 ОГЭ по математике #5Скачать

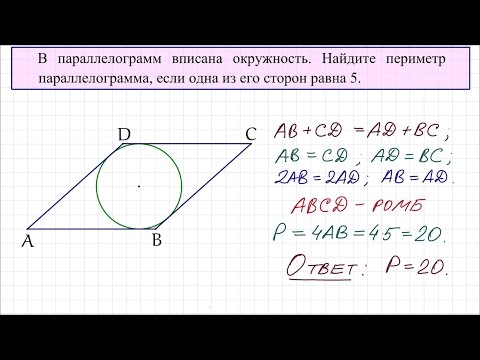
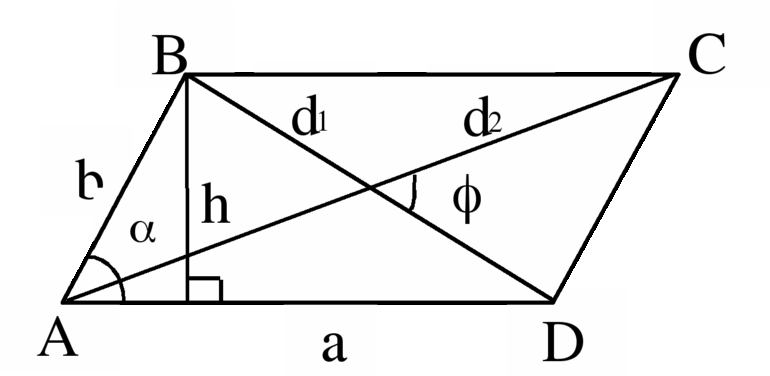
Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

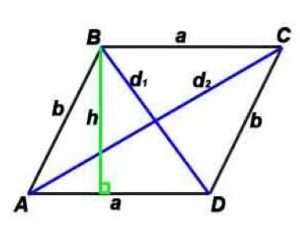
Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
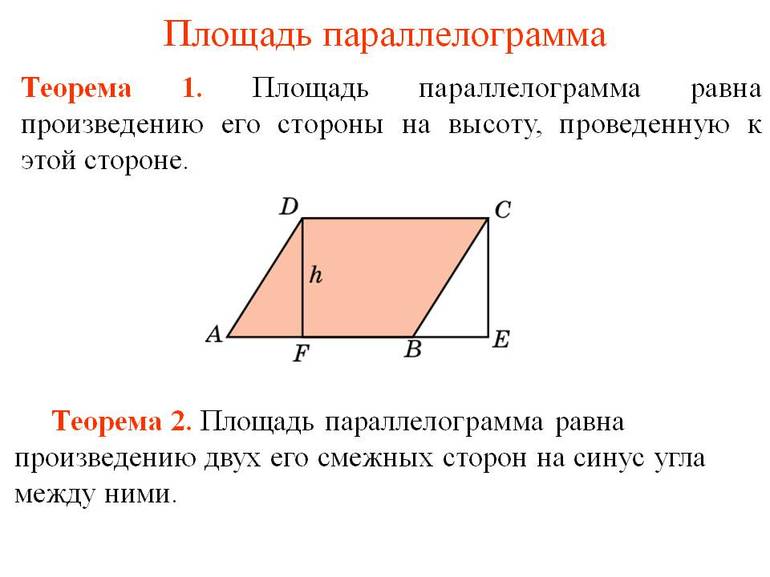
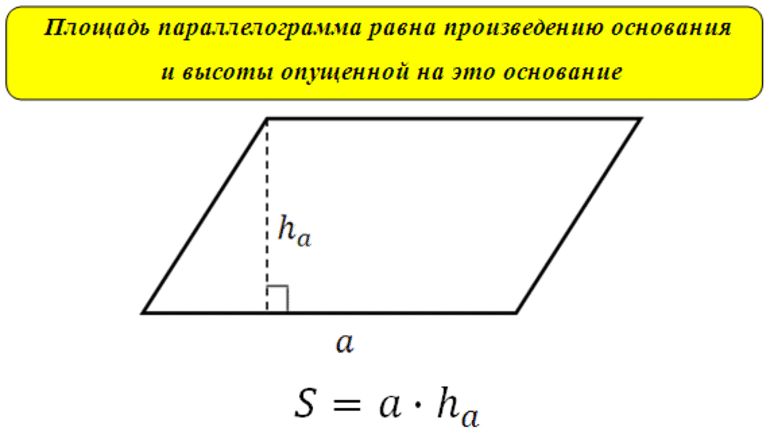
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

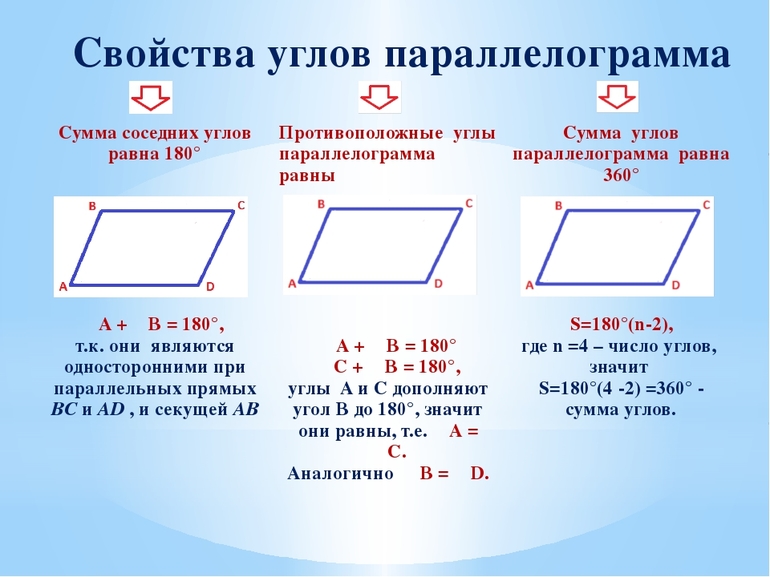
Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
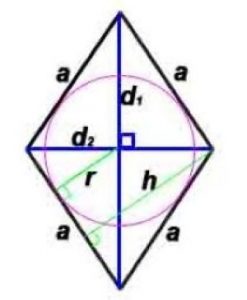
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Видео:№709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограммСкачать

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
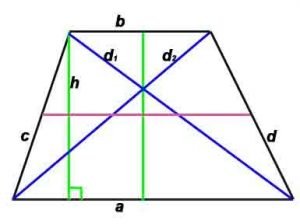
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника— отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
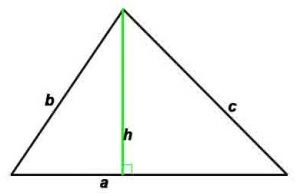
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
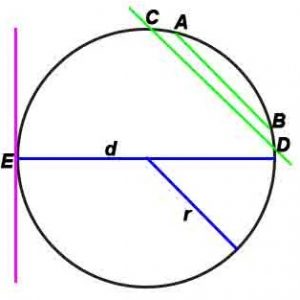
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Видео:Когда в параллелограмм можно вписать окружность. 15 задание ОГЭСкачать

Параллелограмм — его основные свойства, признаки и формулы

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Общие сведения о фигуре

Параллелограмм — это четырехугольник на плоскости, у которого присутствует равенство противоположных сторон, причем они лежат на параллельных прямых. Ромб, прямоугольник и квадрат — его частные случаи. Из него состоят более сложные объемные фигуры. Например, параллелепипед и куб. Высота параллелограмма — отрезок, который является перпендикуляром, проведенным к нижней стороне геометрической фигуры.

Всего можно провести четыре высоты. Две из них можно провести из вершин углов, которые лежат в параллелограмме и являются тупыми. Другие две высоты проводятся из острых углов (находятся вне фигуры). Углы делятся на шесть типов: острые, прямые, тупые, развернутые, выпуклые и полные.

Первый тип, градусная размерность которого меньше 90, является острым. Если значение равно 90, то он является прямым, и соответствует второму типу. В случае, когда выполняется условие 90 2 + b 2 + c 2 + d 2 .

Последний признак можно записать для упрощения расчетов следующим образом: sqr (d1) + sqr (d2) = 2 * (a 2 + b 2 ). Равенство можно упростить, поскольку противоположные стороны равны.

Основные свойства

Для решения задач и проектирования деталей необходимо знать основные свойства параллелограмма. Некоторые из них были получены при доказательстве и следствиях из теорем. К ним относятся следующие:

• Ромб, квадрат и прямоугольник — параллелограммы.
• Противоположные стороны одинаково равны и параллельны.
• Противолежащие углы равны.
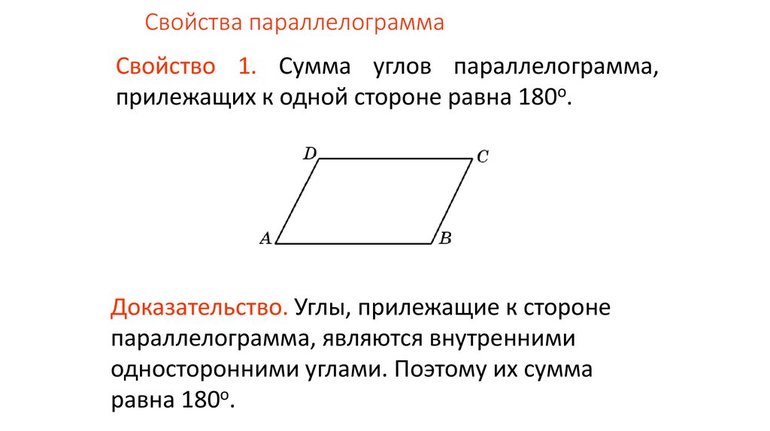
• Суммарное значение градусной меры всех внутренних углов параллелограмма составляет 360.
• Сумма углов, прилегающих к одной из вершин, составляет 180 градусов.
• Диагональ делит фигуру на два треугольника, которые равны между собой по всем признакам.
• Две диагонали (одна — большая, а другая — меньшая) делят параллелограмм на две пары треугольников, которые равны между собой.
• Диагонали фигуры пересекаются, а точка пересечения делит их пополам (через нее можно провести среднюю линию, которая параллельна сторонам).
• Точка пересечения двух диагоналей является симметрией фигуры.
• Биссектрисы соседних углов пересекаются под углом в 90 градусов, а противоположных являются параллельными.
• sqr (d1) + sqr (d2) = 2 * ((a)^2 + (b)^2).

Однако для выполнения расчетов признаков и свойств параллелограмма недостаточно. В некоторых случаях требуется вычислить периметр и площадь фигуры. Соотношения используются не только в учебных заведениях, но и в научных исследованиях. Простым примером является нахождение площади поперечного сечения проводника. Это может понадобиться для дальнейшего вычисления электрического сопротивления.

Определение периметра

Периметром (P) любой фигуры является сумма длин всех ее сторон. Следовательно, для параллелограмма найти это значение является несложным. Базовая формула периметра параллелограмма имеет следующий вид: P = a + b + c + d = 2 * (a + b). Кроме того, существуют и другие соотношения для нахождения этой величины:

1. Если известны одна из сторон и две диагонали.
2. Нахождение периметра через сторону, высоту и синус угла.

В первом случае соотношение для стороны «a» записывается следующим образом: P = 2 * a + sqrt [2 * (d1 * d1 + d2 * d2 — 2 * a^(2))]. Для «b» запись изменяется таким образом: P = 2*b + sqrt [2 * (d1^(2) + d2^(2) — 2 * b^(2))].

Во втором случае, когда известна сторона «а», угол BAD и высота Ha, периметр записывается формулой вида: P = 2 * [a + Ha / sin (BAD)]. Для стороны «b», угла BAD и высоты Hb равенство принимает следующий вид: P = 2 * [b + Hb / sin (BAD)]. Если проанализировать последние два соотношения, то величины «Hb / sin (BAD)» и «Hа / sin (BAD)» являются стороной «b» и «a» соответственно.

Вычисление площади

Площадь параллелограмма (S) — это пространство, которое ограничено его сторонами, и равно произведению одной из сторон на высоту, проведенную к одноименному основанию. Базовая формула нахождения значения S является следующей: S = a * Ha = b * Hb. Кроме того, существует два способа нахождения ее значения, когда известны следующие величины:

1. По сторонам и углу.
2. Две диагонали и синус углов f или g между ними.

Можно записать соотношение следующим образом: S = a * b * sin (BAD) = a * b * sin (ABC). В последнем случае математическая запись площади имеет следующий вид: S = 0,5 * d1 * d2 * sin (f) = 0,5 * d1 * d2 * sin (g). Кроме того, существует формула Герона, которая позволяет вычислить площадь параллелограмма. Для этого необходимо вычислить полупериметр (p) треугольника со сторонами a, b и d: p = P / 2 = (a + b + d). Формула имеет вид: S = sqrt[p * (p — a) * (p — b) * (p — d)].

Соотношения сторон и диагоналей

В некоторых задачах необходимо определить неизвестные длины сторон или диагонали. Можно попытаться вывести соотношения, однако эта процедура занимает некоторое время. Следовательно, проще воспользоваться уже готовыми формулами. Стороны параллелограмма можно определить четырьмя основными выражениями. При этом следует знать следующие величины:

1. Диагонали и угол.
2. Другую сторону и диагонали.
3. Высоту и значение синуса угла в градусах.
4. Площадь и высоту.

В первом случае для вычисления длины стороны «а», следует воспользоваться следующей формулой: a = [sqrt (d1 *d1 + d2 * d2 — 2 * d1 * d2 * cos (f))] / 2 = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (g))] / 2. Значение стороны «b» вычисляется немного иначе: b = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (f))] / 2 = [sqrt (sqr (d1) + sqr (d2) — 2 * d1 * d2 * cos (g))] / 2.

При известных значениях диагоналей и одной из сторон, соотношение имеет более простой вид, чем в первом случае: a = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * b 2 ))] / 2 и b = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * a 2 ))] / 2.

Когда известны высоты и угол BAD, можно найти стороны a и b: a = Hb / sin (BAD) и b = Ha / sin (BAD). Если известны площадь и высота, то соотношение принимает следующий вид: a = S / Ha и b = S / Hb.

Диагональ параллелограмма — отрезок, который соединяет его противоположные внутренние углы. Фигура имеет две диагонали, одна из которых длинная (d1), а другая является короткой (d2). Их можно найти, используя 4 соотношения. Это возможно в том случае, когда известны следующие данные:

• Стороны и косинус угла ABC.
• Cos (BAD) и стороны.
• Одну известную диагональ и стороны.
• Площадь, диагональ и угол между d1 и d2.

В первом случае можно воспользоваться следующими формулами (теорема косинусов): d1 = sqrt[a 2 + b 2 — 2 * a * b * cos (ABC)] и d2 = sqrt[a 2 + b 2 + 2 * a * b * cos (ABC)]. Во втором: d1 = sqrt[a 2 + b 2 + 2 * a * b * cos (BAD)] и d2 = sqrt[a 2 + b 2 — 2 * a * b * cos (BAD)].

Когда известны две стороны и одна из диагоналей, то можно воспользоваться третьим случаем: d1 = sqrt[2 * a 2 + 2 * b 2 — (d2)^2] и d2 = sqrt[2 * a 2 + 2 * b 2 — (d1)^2]. В последнем случае равенства для нахождения диагоналей имеют такой вид: d1 = 2 * S / [(d2) * sin (f)] = 2 * S / [(d2) * sin (g)] и d2 = 2 * S / [(d1) * sin (f)] = 2 * S / [(d1) * sin (g)].

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Параллелограмм и окружность

Существуют определенный тип задач, в которых речь идет о параллелограмме и окружности. Всего бывает два варианта: вписанная и описанная окружности. Следует отметить, что не всегда это возможно. Существуют определенные условия, при которых возможны такие операции. Кроме того, следует обратить особое внимание на дополнительные свойства, которые появляются при комбинации данных фигур. Можно не только чередовать комбинации, но и использовать одновременно.

Для решения сложного типа задач и выполнения расчетов, в некоторых случаях рекомендуется применять вписанные и описанные окружности. Например, при проектировании деталей, необходимо полностью подогнать ее размеры, поскольку они должны быть правильной формы. При помощи окружности (вписанной или описанной) можно выявить ряд дефектов, которые могут привести к некорректной работе механизма.

Круг и прямоугольник

Главное условие: любой четырехугольник можно вписать в окружность, когда сумма его двух противоположных углов составляет 180 градусов. У параллелограмма есть одно свойство: сумма углов, которые прилегают к любой из вершин, составляет 180 градусов. Кроме того, сумма всех его углов составляет 360, а, следовательно, сумму противоположных углов составляет 360 — 180 = 180 (градусов).

Однако при попытке описать около него окружность ничего не выйдет, поскольку есть одно свойство: противоположные углы у него равны. Ими могут быть тупые и острые. Сумма градусной меры тупых углов будет больше 180, а острых — меньше. Когда противоположные углы будут равны 90, то значит их сумма составит 180. В этом случае нужно рассматривать частный случай — прямоугольник. Появляется очень важное свойство: диагонали прямоугольника пересекаются и точкой пересечения (центром окружности) делятся пополам, а также являются диаметрами окружности.

Для нахождения радиуса окружности, следует воспользоваться следующим соотношением (при условии, что известны стороны прямоугольника): R = [sqrt (a 2 + b 2 )] / 2 = d / 2. Величина «d» является диаметром.

Ромб и квадрат

В параллелограмм также можно вписать окружность. Однако для этого необходимо выполнение определенного условия. Оно заключается в следующем: суммы противолежащих сторон параллелограмма должны быть равны. Нужно отметить, что это выполняется только для ромба и квадрата.

Ромбом называется параллелограмм, стороны которого равны, а углы не равны 90 градусов. Квадрат — геометрическая фигура, у которой все стороны и углы равны. Из последнего определения можно найти значение градусной меры одного угла: 360 / 4 = 90. Последняя фигура является частным случаем ромба. Радиус окружности находится с помощью формулы: r = S / p = 0,5 * H. В этом соотношении переменные S, p и H — площадь, полупериметр и высота соответственно. Для нахождения S можно воспользоваться такими соотношениями:

• Известны длина стороны (а) и высота (H): S = a * H.
• Через диагонали d1 и d2: S = d1 * d2 / 2.

Полупериметром фигуры называется половина от значения ее периметра. Соотношение записывается таким образом: p = P / 2 = 4 * a.

Таким образом, знать основные свойства и признаки параллелограмма необходимо, поскольку от этого может зависеть не только качество сдачи экзаменов, решения задач, но и проектирование различных деталей.

🎥 Видео

Четыре окружности в параллелограмме | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Свойства параллелограмма. 8 класс.Скачать

6 способов построения параллелограмма.Скачать

Окружность Параллелограмм РомбСкачать

Параллелограмм. Свойства. Периметр.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 8 класс за 1 час | Математика | УмскулСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать