 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Как построить прямую? Как построить график прямой или линейной функции?
- ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
- ПРАКТИЧЕСКАЯ ЧАСТЬ
- 💥 Видео
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Параллельность прямой к плоскостиСкачать

График линейной функции
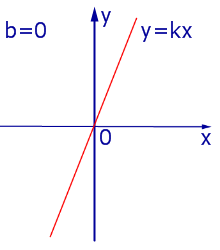
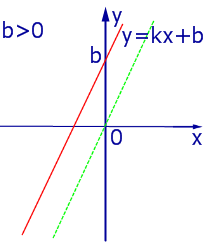
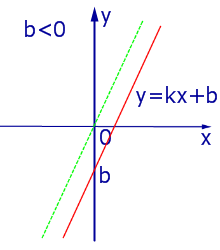
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
 |
| Рис.1 |
 |
| Рис.2 |
 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
| Рис.4 |
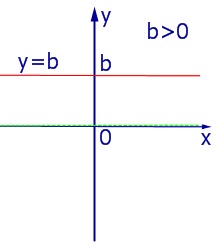 |
| Рис.5 |
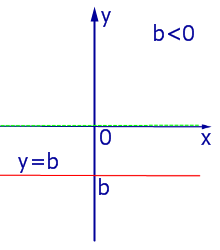 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Параллельные прямые циркулемСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Проецирование прямой общего положенияСкачать  График линейной функции, его свойства и формулыО чем эта статья: Статья находится на проверке у методистов Skysmart. Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Понятие функцииФункция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции. Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек. Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать  Понятие линейной функцииЛинейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат. Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки. Если известно конкретное значение х, можно вычислить соответствующее значение у. Нам дана функция: у = 0,5х — 2. Значит:
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции. Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат. Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби. Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b». Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart! Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать  Свойства линейной функции
Видео:Математика без Ху!ни. Уравнение касательной.Скачать  Построение линейной функцииВ геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y. Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график: В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая. В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3). Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /2x + 3, y = -x + 3. В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая. Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3). Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2. Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые. При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты. Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b. Если k 0, то график функции y = kx + b выглядит так: 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»> Если k > 0 и b > 0, то график функции y = kx + b выглядит так: 0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»> Точки пересечения графика функции y = kx + b с осями координат:
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать  Решение задач на линейную функциюЧтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся! Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Видео:7 класс. Задайте формулой линейную функцию, параллельную данной и проходящую через точку NСкачать  Как построить прямую? Как построить график прямой или линейной функции?ТЕОРЕТИЧЕСКАЯ ЧАСТЬХочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ Для начала определимся с формулой прямой или линейной функции ее записывают по-разному, но смысл от этого не меняется:y=kx+b; y=ax+b; ax+by+c=0; a и k — называются угловыми коэффициентами, а число b – свободным членом. Если a>0 или k>0, то график прямой возрастающий;
Если a Параллельные прямые имеют равные угловые коэффициенты и разные свободные члены b не равно с.
Перпендикулярные прямые (это прямые которые пересекаются под 90 градусов), произведение их угловых коэффициентов будет равняться -1.
b — указывает где график прямой пересекает ось y. Алгоритм построения прямой. ПРАКТИЧЕСКАЯ ЧАСТЬРассмотрим на примере №1: берем 2 точки чтобы построить график прямой Видно что a=1 (график прямой возрастает),
Пример №2: Выразим во всех уравнениях y, получим Ответ: Параллельные прямые 1) и 6); 2) и 3); 4) и 5), так как коэффициенты их равны. 💥 ВидеоПрямая пропорциональность и её график. Алгебра, 7 классСкачать  Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать  КАК ПОСТРОИТЬ ПРЯМУЮ ПАРАЛЛЕЛЬНУЮ ДАННОЙ ПРЯМОЙ? Примеры | МАТЕМАТИКА 6 классСкачать  Уравнение касательной, параллельной заданной прямой.Скачать  Построение прямой параллельной данной прямой проходящей через точку вне данной прямойСкачать  Уравнение параллельной прямойСкачать  Прямая параллельная плоскостиСкачать  Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать  Параллельные прямые. 6 класс.Скачать  |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.










 y=ax+b, a>0
y=ax+b, a>0 a
a Признак параллельности прямых a=k
Признак параллельности прямых a=k Перпендикулярные прямые k*a=-1
Перпендикулярные прямые k*a=-1
 y=ax+b, a>0
y=ax+b, a>0