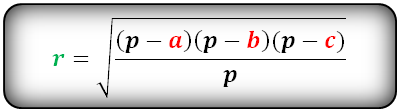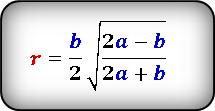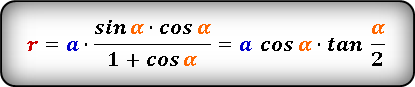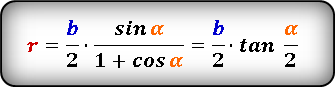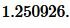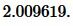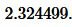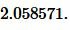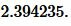- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в прямоугольный треугольник
- Как найти диаметр вписанной окружности равнобедренного треугольника
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в прямоугольный треугольник
- 🎥 Видео
Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

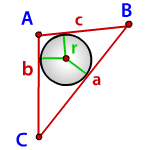
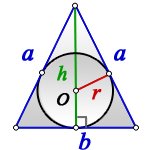
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

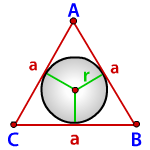
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

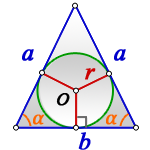
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Радиус вписанной окружности в треугольник
Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.
Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.
Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.
В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.
Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.
Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.
Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.
Всего различают четыре вида треугольников:
- Разносторонний / любой
- Правильный / равносторонний
- Равнобедренный / равнобочный
- Прямоугольный / прямой
Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в любой треугольник через площадь и полупериметр
S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в правильный треугольник
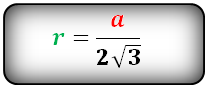
- Радиус вписанной окружности в правильный треугольник через сторону
a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.
Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.
Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.
В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.
Видео:№694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать
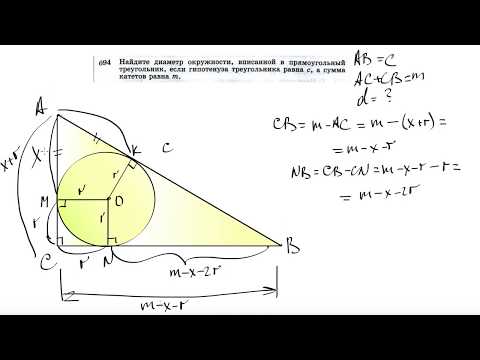
Как найти диаметр вписанной окружности равнобедренного треугольника
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
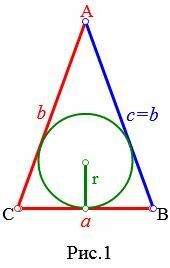 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
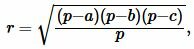 | (1) |
где полупериметр p вычисляется из формулы:
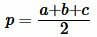 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac , ) | (3) |
| ( small p-a=frac -a ) ( small =frac , ) | (4) |
| ( small p-b=p-c=frac -b ) ( small =frac . ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
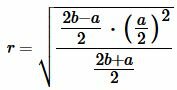 , , |
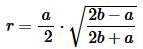 . . | (6) |
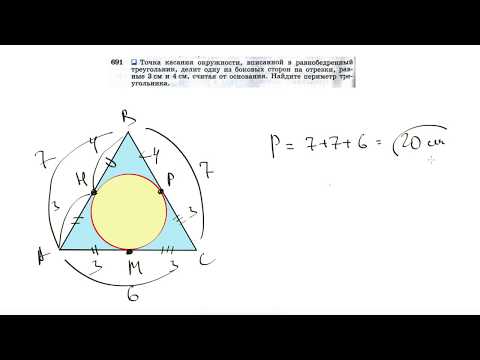
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
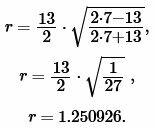 |
Ответ:
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
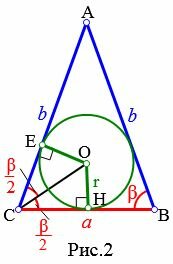 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac . ) Для прямоугольного треугольника OCH можно записать:
| ( small frac =frac >=mathrm frac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrm frac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
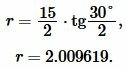 |
Ответ:
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
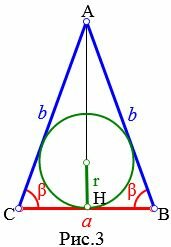 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac =frac > = cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrm frac =frac cdot mathrm frac ) ( small =b cos beta cdot mathrm frac ) |
| ( small r=b cdot cos beta cdot mathrm frac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
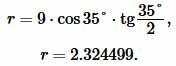 |
Ответ:
Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
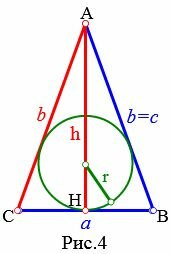 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
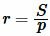 , , | (13) |
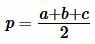 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( frac right)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac +b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac > > ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
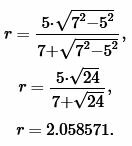 |
Ответ:
Видео:8 класс. ОГЭ. Найти диаметр окружностиСкачать

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
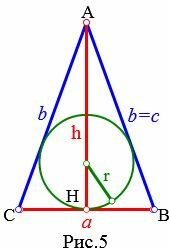 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt ) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac > >) ( small =frac +h^2-h^2>> cdot sqrt + sqrt +h^2-h^2>>) ( small = large frac > cdot sqrt +frac >) |
| ( small r=large frac >) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
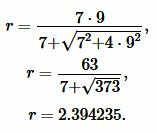 |
Ответ:
Видео:Радиус описанной окружностиСкачать

Все формулы для радиуса вписанной окружности
Видео:Радиус и диаметрСкачать

Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

Радиус вписанной окружности в треугольник
Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.
Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.
Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.
В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.
Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.
Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.
Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.
Всего различают четыре вида треугольников:
- Разносторонний / любой
- Правильный / равносторонний
- Равнобедренный / равнобочный
- Прямоугольный / прямой
Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в любой треугольник через площадь и полупериметр
S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в правильный треугольник через сторону
a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.
Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.
Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.
В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.
🎥 Видео
Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать

Нахождение диаметра описанной окружностиСкачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать