Дивергенции вектора электрического поля (3 видео)

Дивергенция векторного поля. Теорема Гаусса в дифференциальной форме

4. Дивергенция векторного поля. Теорема Гаусса в дифференциальной форме

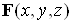
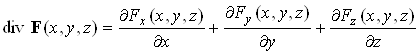
Произвольному векторному полю (т.е. некоторой векторной функции , заданной в точках (x,y,z) некоторой области пространства) можно сопоставить скалярную функцию, называемую дивергенцией поля F. Эта функция обозначается символом «div» и определяется соотношением

. (1.4.1)

Физический смысл дивергенции следует из формулы, доказываемой в курсе высшей математики:

. (1.4.2)

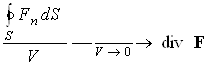
При предельном переходе объем V и его поверхность S стягиваются в точку наблюдения, в которой вычисляется дивергенция. Согласно (1.4.1), поток напряженности E через любую бесконечно малую сферу, внутри которой нет зарядов, – тождественный нуль. Поэтому из (1.4.2) следует, что в точках с нулевой плотностью зарядов (r=0) дивергенция E равна нулю. Рассмотрев поток через малую сферу V вокруг точки, в которой дивергенция напряженности не равна нулю, можно показать с помощью (1.4.1) и (1.4.2) , что в такой точке объемный заряд есть, поэтому точки, в которых дивергенция напряженности отлична от нуля, являются источниками силовых линий.

В курсе математики доказывается теорема Остроградского-Гаусса (была установлена К. Гауссом в 1844 независимо от М.В. Остроградского, доказавшего ее в 1839):

. (1.4.3)

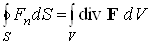
Здесь V – произвольный объем, ограниченный поверхностью S. Применим теорему (1.4.3) к потоку электростатического поля. С учетом (1.4.1) получим:

. (1.4.4)

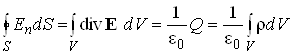
Из равенства интегралов ввиду произвольности объема V следует равенство подынтегральных выражений, т.е. теорема Гаусса в дифференциальной форме (А. Пуассон, 1850 г.):

. (1.4.5)

Содержание

Теорема Гаусса для электростатического поля. Поток и дивергенция вектора Е
Электростатическая теорема Гаусса в дифференциальной форме. Дивергенция
Пример 1
Пример 2
Решение
Добавить комментарий Отменить ответ
🔍 Видео

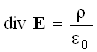
Видео:Дивергенция векторного поляСкачать

Теорема Гаусса для электростатического поля. Поток и дивергенция вектора Е

Рис. 12.3. Однородное поле Ё изображено параллельными силовыми линиями. Штриховыми линиями изображена проекция площади ДS на плоскость, перпендикулярную силовым линиям поля

Рис. 12.4. К определению потока напряженности через неплоекую поверхность 5, когда поле Е неоднородно

Рассмотрим элементарную площадку dS, которую пронизывают линии напряженности (рис. 12.3). Пусть п — единичный вектор, перпендикулярный площадке AS и направленный под углом а к вектору Ё. Тогда число линий напряженности, пронизывающих элементарную площадку AS, равно Е AS cosa = E_nAS, где Е_п — проекция вектора Ё на нормаль п к площадке dS.

Величина ДФ_Е = ?„AS = Е AS cosa = — Ё AS называется потоком вектора напряженности электростатического поля через площадку AS. Здесь AS = AS п — вектор, модуль которого равен AS; его направление совпадает с направлением п к площадке. Отметим, что выбор направления вектора И условен: его можно было направить в противоположную сторону (рис. 12.3).

Если поле неоднородно и поверхность S неплоская (рис. 12.4), то, разбивая поверхность на участки АД,- (/ = 1, п) так, чтобы каждый элемент AS,- был плоским и электрическое поле в пределах элемента было однородным, для потока напряженности через всю поверхность получаем

где E_t — напряженность поля, отвечающая векторному элементу площади поверхности Д5). При Д5,-—»0 сумма переходит в интеграл по всей поверхности и равенство становится точным:

Поток вектора Е через произвольную замкнутую поверхность S, т.е. через поверхность, ограничивающую некоторую область пространства, определяется по формуле

где знак ф показывает, что интеграл берется по замкнутой поверхности. s

Для наглядного изображения электростатического поля через единичную площадку, перпендикулярную силовым линиям поля, будем проводить силовые линии N_E, число которых равно модулю потока Ф_? вектора напряженности.

Рис. 12.5. К выбору вектора dS = dSn элемента замкнутой поверхности S

В случае замкнутой поверхности S принято брать нормаль п , внешнюю по отношению к области, охватываемой этой поверхностью, т.е. внешнюю нормаль (рис. 12.5). Знак потока Ф_? определяется следующим образом. Если силовые линии выходят из объема (рис. 12.5, угол а я/2 , т.е. cosa г

Рис. 12.6. К выводу теоремы Гаусса

Рассмотрим воображаемую замкнутую сферическую поверхность S радиуса г, в центре которой помещен точечный положительный заряд q. Силовые линии заряда q центрально-симметричны (рис. 12.6). В соответствии с формулой (12.11а) в каждой точке этой поверхности проекция вектора Е на внешнюю нормаль

Следовательно, поток вектора Е через поверхность S

Выражение (12.116) не зависит от /*. Так как силовые линии нигде не пересекаются, то их число будет таким же через любую замкнутую поверхность, охватывающую заряд q.

Если заряд положителен, то на нем начинается число линий

Для отрицательного заряда линии идут из бесконечности, заканчиваясь на нем:

Количество линий при этом N_E K >0, т.е. неотрицательно, так как q Теорема Гаусса для вектора Е в дифференциальной форме. При рассмотрении поля, создаваемого макроскопическим зарядом, заряд считают распределенным в пространстве непрерывно с конечной объемной плотностью р. Тогда можно считать, что каждый элементарный объем AV представляет собой точечный заряд pAV.

Разделим поток вектора Е через замкнутую поверхность S на объем AV, ограниченный данной поверхностью:

и будем стягивать эту поверхность в точку. Полученная скалярная величина называется дивергенцией вектора Е:

Можно показать, что в декартовой системе координат

Согласно теореме Остроградского из векторного анализа

Сопоставив уравнения (12.11) и (12.12), сформулируем теорему Гаусса (12.11) в дифференциальной форме: дивергенция вектора Е в некоторой точке электростатического поля равна объемной плотности электрического заряда р в этой точке, деленной на ?₀:

Те точки поля, где div? положительна, называются источниками векторного поля (положительные заряды), а те точки, где она отрицательна, — стоками (отрицательные заряды).

Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

Электростатическая теорема Гаусса в дифференциальной форме. Дивергенция

Уравнение, связывающее поток вектора напряженности поля через замкнутую поверхность и заряд, помещенный внутри этой поверхности, представлено в интегральной форме:

Устремляя к нулю объем, ограниченный поверхностью интегрирования, вокруг какой-то точки и предполагая, что плотность электрического заряда это непрерывная функция координат, можно легко перейти к дифференциальной формулировке того же закона:

В данном уравнении ρ – плотность заряда в точке, вокруг которой стягивается замкнутая поверхность (стягивается так, что любой линейный размер ограничиваемого ею объема стремится к нулю).

Указанное требование предельного перехода (V→0) физически не осуществимо, так как оно равносильно требованию непрерывности ρ как функции координат.

И правда, когда объем V становится настолько мал, что внутри него оказывается небольшое число электронов или атомов, макроскопическое понятие средней плотности заряда теряет смысл. Стремление линейных размеров и объема к нулю понимается здесь, как и во всей макроскопической динамике, в том смысле, что рассматриваемые малые расстояния и объемы могут с точки зрения математического описания поля считаться ничтожными, вместе с тем они должны оставаться еще настолько большими, чтобы не теряли смысла понятия макроскопической физики, рассматривающей вещество как сплошную среду.

Отношение в левой стороне выражения (1) носит название расхождение или дивергенция вектора Е:

Из самого определения выступает физический смысл дивергенции какого-либо физического вектора. В самом деле поток, исходящий из объема, ограниченного данной поверхностью, указывает на существование источников этого потока внутри поверхности и количественно выражает их «мощность» (силу, интенсивность). Отношение полного исходящего потока к объему, который ограничивает поверхность, характеризует объемную плотность источников потока.

Давайте разберем небольшой пример, демонстрирующий наглядное представление о дивергенции.

Представим себе в комнате трубку с разреженным газом, светящимся при электрическом разряде (в нем возникает световой поток) или зажженную свечу. В комнате воздух прозрачен, а снаружи пропитан туманом и дымом (световой поток поглощается). Внутри газоразрядной трубки или пламени свечи дивергенция вектора плотности светового потока положительна, в комнатном воздухе дивергенция равна нулю, а за окном дивергенция отрицательна.

Выбрав ту или иную систему координат, можно записать дифференциальную операцию div E непосредственно из ее определения (2). В декартовой системе координат дивергенция будет иметь вид:

По самому определению дивергенция это скаляр, а сама дифференциальная операция применяется к вектору. Можно заметить, что формально результат, приведенный в формуле (3) можно представить как скалярное произведение векторов набла и Е:

Электростатическая теорема Гаусса в дифференциальной форме формулируется как:

Вывод следует из формул (1) и (2).

Пример 1

Напряженность поля изменяется по закону E_x = E₀(α/x), E_y = 0, E_z = 0 при α

Это поле плоского конденсатора с отрицательным объемным зарядом, поэтому напряженность поля убывает по мере удаления от положительной пластины (в направлении Е_Х).

Пример 2

Условия те же, что и в предыдущем примере, но напряженность поля изменяется по закону:

Решение

Непосредственно дифференцируя, находим:

Данное поле совпадает с полем заряженного цилиндра (r_ц Posted in Основы электричества

Добавить комментарий Отменить ответ

Автоматизация технологических процессов (182)
Альтернативная энергетика (34)
Интернет вещей (IoT) (135)
Микроконтроллеры (33)
Моделирование электромеханических систем (22)
Новости партнеров (1)
Новости электроники (222)
Основы электричества (44)
Реактивная мощность (13)
Робототехника (53)
Станки с ЧПУ (46)
Схемотехника (133)
Теория автоматического управления (17)
Электрика в быту (61)
Электрические машины и аппараты. Трансформаторы (82)
Электропривод (130)
Электроснабжение (95)
Электротехника (143)
Энергосбережение (106)

Магнитные пускатели — 142 656
Логические элементы и их схемная реализация — 115 972
В чем разница между NPN и PNP транзисторами? — 107 475
Что такое активная, реактивная и полная мощность — 96 241
Ввод и распределение электроэнергии в многоквартирном доме — 89 796
Соотношение между фазными и линейными напряжениями. Номинальные напряжения — 89 159
Что такое категории надежности электроснабжения? — 84 417
11 мифов о Bluetooth 5.0 — 79 451
Мощность трехфазной сети — 72 997
Что такое цветовая маркировка шин и проводов и зачем она нужна — 68 840