Диагонали в четырехугольнике равны докажите что его средние линии перпендикулярны

Докажите теорему: если средние линии четырёхугольника равны, то диагонали четырёхугольника перпендикулярны.

Примечание. Средней линией четырёхугольника называют отрезок, соединяющий середины его противоположных сторон.

Середины противоположных сторон четырёхугольника являются вершинами параллелограмма Вариньона, а если отрезки, соединяющие их, равны, то равны диагонали параллелограмма, а значит, этот параллелограмм является прямоугольником. По следствию из теоремы Вариньона стороны полученного четырёхугольника параллельны диагоналям исходного, а так как стороны прямоугольника перпендикулярны, перпендикулярны и диагонали исходного четырёхугольника.

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Средние линии черырехугольников

В работе приводятся теоретические факты и расматриваются задачи на среднии линии четырехугольников.

Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

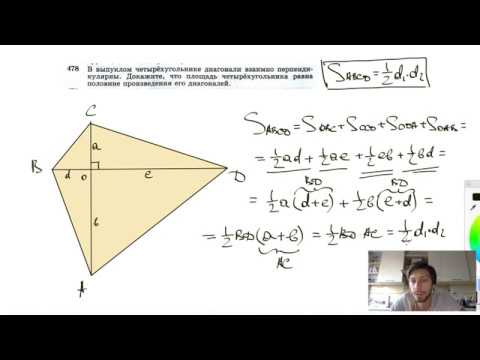
Скачать:

Предварительный просмотр:

Видео:№797. Докажите, что средняя линия трапеции проходит через середины диагоналей.Скачать

Подписи к слайдам:

Средние линии четырехугольников и их свойства Выполнил: Матвеев Дмитрий Учитель: Рычкова Татьяна Викторовна Лицей «Дубна» 9ИМ 2007 Средние линии и Параллелограмм Вариньона Другие свойства средней линии четырехугольника Краткий перечень всех теорем и свойств

Что такое параллелограмм Вариньона? Это параллелограмм, вершины которого являются серединами сторон четырехугольника Иначе: это параллелограмм, диагоналями которого являются средние линии четырехугольника

A B C D N M L K P Доказательство: Соединим точки K, L, M, N и проведем диагональ АС; В ∆ACD NM – средняя линия, значит NM  AC и NM=1/2 AC; В ∆ABC KL – средняя линия, значит KL  AC и KL=1/2 AC; NM=1/2 AC=KL, NM  AC  KL, значит четырехугольник KLMN ‑ параллелограмм. A L B M C D K P N Доказательство: Соединим точки K, L, M, N и проведем диагональ DB; В ∆CDB NM – средняя линия, значит NM  DB и NM=1/2 DB; В ∆ADC KL – средняя линия, значит KL  DB и KL=1/2 DB; NM=1/2 DB=KL, NM  DB  KL, значит четырехугольник KLMN ‑ параллелограмм. Докажем, что KLMN – параллелограмм Вариньона, при KM и NM – средних линиях ABCD.

А значит… Так как четырехугольник KLMN – параллелограмм Вариньона, то его диагонали в точке пересечения делятся пополам Средние линии любого четырехугольника делятся пополам

Следствия: 1. Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Доказательство: Так как в параллелограмме Вариньона равные средние линии являются равными диагоналями, то этот параллелограмм – прямоугольник, а вокруг него всегда можно описать окружность, значит его вершины лежат на одной окружности.

Следствия: 2. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Доказательство: Так как NL┴KM и NL с KM диагонали в параллелограмме KLMN , то KLMN – ромб. По этому KL = LM = MN = NK . Так как AC =2 KL и BD =2 NK , то AC = BD . A K B L C M D N P O A P K C D M N L B

Следствия: A K B L C M D N P O A P K C D M N L B 3. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Доказательство: Так как AC =2 MN =2 KL , BD =2 NK =2 ML и AC = BD , то KL = LM = MN = NK . Значит KLMN – ромб, а в ромбе диагонали перпендикулярны, то есть NL┴KM.

Для примера: Решая такую задачу, пришлось бы сильно потрудится, не зная одно из свойств параллелограмма Вариньона:

Какова же площадь параллелограмма Вариньона? Доказательство для выпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

Какова же площадь параллелограмма Вариньона? Доказательство для невыпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

S KLMN =1/2 S ABCD Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Следствие: площади четырехугольников с равными средними линиями равны. Следствие: площадь четырехугольника равна произведению его средних линий на синус угла между ними.

Для примера: Теперь можно решить задачу в два шага: 1. S пар. Вариньона равна 15*18=270 см в кв. 2. S ABCD = 2*270= =540 см в кв.

Какова длина средней линии? A D C F B G E Пусть EF – средняя линия четырехугольника ABCD (EA=ED, FB=FC , AB не параллельна DC); Тогда : NL= ND + DA + AL и NL = NC + CB + BL Сложим эти равенства и получим: 2NL = DA + CB Значит вектора 2NL, DA и CB являются сторонами треугольника При параллельном переносе векторов DC и 2EF получатся равные им вектора BG и AG , которые вместе с вектором AB образуют ∆ AGB , где по неравенству треугольника получим: AG<=AB+BG , откуда : EF<1/2 (AB+CD). Если же AB параллельна DC , то ABCD — трапеция (или параллелограмм) с основаниями AB и DC , тогда: EF = 1/2 (AB+CD). Значит EF< = 1/2 (AB+CD) , то есть: Длина средней линии четырехугольника не превышает полусуммы длин сторон, не соединенных ею.

Краткий перечень всех теорем и свойств: Средние линии любого четырехугольника делятся пополам Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Площади четырехугольников с равными средними линиями равны. Площадь четырехугольника равна произведению его средних линий на синус угла между ними. Длина средней линии четырехугольника не превышает полусуммы длин сторон, не соединенных ею. Если 4-хугольнике две противоположные стороны равны и не параллельны, то прямая, включающая в себя среднюю линию, не проходящую через эти стороны, образует с продолжениями этих сторон равные углы

Видео:Диагонали четырехугольника равны 4 и 5.Скачать

Please wait.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

We are checking your browser. mathvox.ru

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6c87eee15c20160a • Your IP : 85.95.179.65 • Performance & security by Cloudflare

📸 Видео

Геометрия Докажите, что если диагонали равнобокой трапеции перпендикулярны, то ее высота равнаСкачать

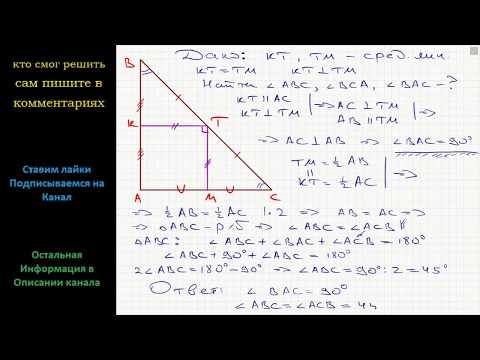
Геометрия Найдите углы треугольника, две средние линии которого равны и перпендикулярныСкачать

Геометрия Докажите, что если высота равнобокой трапеции равна ее средней линии, то диагоналиСкачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать

Геометрия Докажите, что средняя линия трапеции параллельна основаниям и равна их полусуммеСкачать

№389. Докажите, что трапеция равнобедренная, если: а) углы при основании равны (ИСПРАВЛЕН п.б)Скачать

Теорема о средней линии трапецииСкачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

8 класс, 25 урок, Средняя линия треугольникаСкачать

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

8 класс, 6 урок, ТрапецияСкачать

Геометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать